Trong thế giới bóng đá, chiến thắng là mục tiêu tối thượng. Để đạt được mục tiêu này, các huấn luyện viên và cầu thủ cần có chiến lược phù hợp, kỹ năng cá nhân và sự phối hợp nhuần nhuyễn. Tương tự như vậy, trong lĩnh vực toán học, việc Giải Và Biện Luận Hệ Bất Phương Trình cũng đòi hỏi sự sáng tạo, kỹ thuật và tư duy logic.
Bài viết này sẽ giúp bạn hiểu rõ hơn về khái niệm hệ bất phương trình, các phương pháp giải và biện luận, đồng thời cung cấp những bí quyết chiến thắng trong việc giải quyết các bài toán liên quan. Hãy cùng khám phá!
Hệ Bất Phương Trình Là Gì?
Hệ bất phương trình là một tập hợp các bất phương trình có chung một tập hợp các ẩn số. Ví dụ, hệ bất phương trình sau đây gồm hai bất phương trình với hai ẩn số x và y:
x + 2y > 5
3x - y < 10Để giải hệ bất phương trình, chúng ta cần tìm tập hợp các giá trị của các ẩn số thỏa mãn tất cả các bất phương trình trong hệ.
Các Phương Pháp Giải Hệ Bất Phương Trình
Có nhiều phương pháp giải hệ bất phương trình, mỗi phương pháp phù hợp với một loại hệ cụ thể. Dưới đây là một số phương pháp phổ biến:
1. Phương Pháp Biểu Diễn Hình Học
Phương pháp này dựa vào việc biểu diễn các bất phương trình trên hệ trục tọa độ. Mỗi bất phương trình sẽ tương ứng với một miền nghiệm, tức là tập hợp các điểm thỏa mãn bất phương trình đó. Miền nghiệm của hệ bất phương trình chính là giao của các miền nghiệm của từng bất phương trình.
Ví dụ:
Để giải hệ bất phương trình:
x + 2y > 5
3x - y < 10Chúng ta biểu diễn từng bất phương trình trên hệ trục tọa độ.
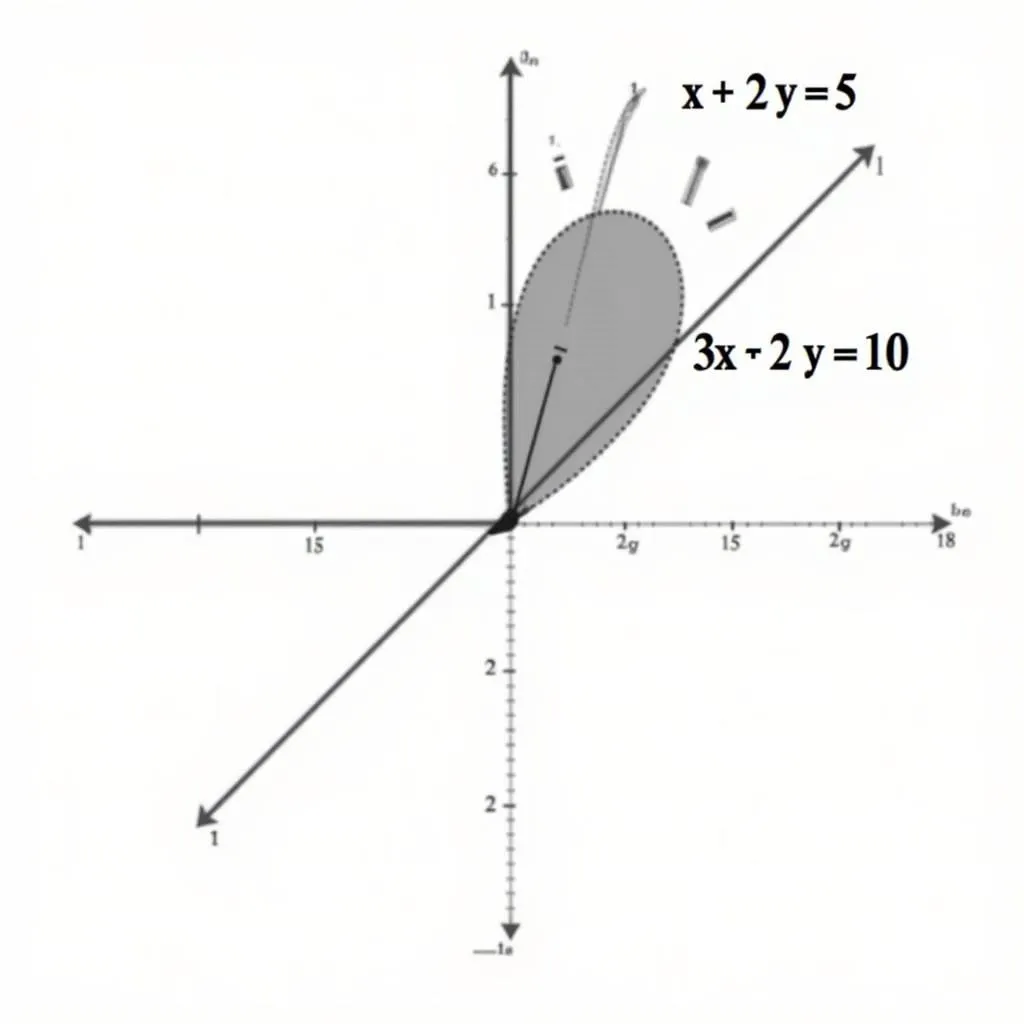 Biểu diễn Hình Học Hệ Bất Phương Trình
Biểu diễn Hình Học Hệ Bất Phương Trình
Miền nghiệm của hệ bất phương trình là phần giao nhau của hai miền nghiệm màu xanh lá cây và màu vàng, được biểu diễn bởi màu xanh lá cây đậm.
2. Phương Pháp Biến Đổi Tương Đương
Phương pháp này dựa vào việc biến đổi hệ bất phương trình về dạng đơn giản hơn, sao cho các nghiệm của hệ ban đầu và hệ mới là giống nhau. Các phép biến đổi tương đương thường được sử dụng là:
- Cộng (trừ) hai vế của một bất phương trình với một biểu thức cùng dấu.
- Nhân (chia) hai vế của một bất phương trình với một biểu thức dương.
- Đổi dấu hai vế của một bất phương trình.
Ví dụ:
Để giải hệ bất phương trình:
x + 2y > 5
3x - y < 10Chúng ta có thể biến đổi hệ này về dạng đơn giản hơn bằng cách cộng hai vế của bất phương trình thứ nhất với 3 lần bất phương trình thứ hai:
(x + 2y) + 3(3x - y) > 5 + 3(10)Sau khi rút gọn, ta thu được:
10x - y > 35Bất phương trình này tương đương với bất phương trình thứ hai của hệ ban đầu. Do đó, nghiệm của hệ ban đầu chính là nghiệm của hệ sau:
x + 2y > 5
10x - y > 353. Phương Pháp Sử Dụng Ma Trận
Phương pháp này phù hợp với hệ bất phương trình tuyến tính, tức là các bất phương trình trong hệ đều có dạng tuyến tính.
Chúng ta có thể viết hệ bất phương trình tuyến tính dưới dạng ma trận:
Ax > bTrong đó A là ma trận hệ số, x là vector ẩn số, b là vector hằng số.
Để giải hệ bất phương trình, chúng ta có thể sử dụng các phương pháp giải hệ phương trình tuyến tính, chẳng hạn như phương pháp Gauss-Jordan, để tìm nghiệm của hệ Ax = b. Sau đó, chúng ta cần kiểm tra xem nghiệm đó có thỏa mãn các điều kiện của bất phương trình Ax > b hay không.
Biện Luận Hệ Bất Phương Trình
Biện luận hệ bất phương trình là việc xác định số nghiệm của hệ, tức là xác định số bộ giá trị của các ẩn số thỏa mãn tất cả các bất phương trình trong hệ.
Số nghiệm của hệ bất phương trình phụ thuộc vào nhiều yếu tố:
- Số lượng bất phương trình trong hệ.
- Loại bất phương trình trong hệ.
- Các giá trị của hệ số trong các bất phương trình.
Để biện luận hệ bất phương trình, chúng ta thường sử dụng các phương pháp:
- Phương pháp biểu diễn hình học: Dựa vào vị trí tương đối của các miền nghiệm của các bất phương trình trong hệ, ta có thể xác định số nghiệm của hệ.
- Phương pháp biến đổi tương đương: Dựa vào các phép biến đổi tương đương, ta có thể đưa hệ bất phương trình về dạng đơn giản hơn, từ đó xác định số nghiệm của hệ.
- Phương pháp sử dụng ma trận: Dựa vào tính chất của ma trận hệ số, ta có thể xác định số nghiệm của hệ.
Bí Kíp Chiến Thắng Khi Giải Và Biện Luận Hệ Bất Phương Trình
- Hiểu rõ khái niệm và các phương pháp giải: Hãy đảm bảo bạn hiểu rõ định nghĩa của hệ bất phương trình, các phương pháp giải và biện luận.
- Luyện tập thường xuyên: Việc luyện tập thường xuyên là chìa khóa để nâng cao kỹ năng giải và biện luận hệ bất phương trình.
- Áp dụng các chiến lược giải quyết vấn đề: Hãy phân tích kỹ đề bài, xác định loại hệ bất phương trình, lựa chọn phương pháp phù hợp và áp dụng các kỹ thuật biến đổi tương đương.
- Kiểm tra kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
- Tìm kiếm sự trợ giúp: Nếu gặp khó khăn, đừng ngại ngần hỏi giáo viên, bạn bè hoặc tìm kiếm tài liệu tham khảo.
Câu hỏi thường gặp
1. Hệ bất phương trình có bao nhiêu nghiệm?
Số nghiệm của hệ bất phương trình phụ thuộc vào vị trí tương đối của các miền nghiệm của các bất phương trình trong hệ. Có thể có vô số nghiệm, một số nghiệm hữu hạn hoặc không có nghiệm.
2. Làm sao để biết hệ bất phương trình có nghiệm hay không?
Để biết hệ bất phương trình có nghiệm hay không, ta có thể biểu diễn các bất phương trình trên hệ trục tọa độ và xem xét vị trí tương đối của các miền nghiệm. Nếu các miền nghiệm có điểm chung thì hệ có nghiệm.
3. Có những loại hệ bất phương trình nào?
Có nhiều loại hệ bất phương trình, chẳng hạn như hệ bất phương trình tuyến tính, hệ bất phương trình bậc hai, hệ bất phương trình chứa giá trị tuyệt đối.
4. Hệ bất phương trình có ứng dụng nào trong thực tế?
Hệ bất phương trình được ứng dụng trong nhiều lĩnh vực như kinh tế, tài chính, khoa học máy tính, kỹ thuật… Ví dụ, trong kinh tế, ta có thể sử dụng hệ bất phương trình để tối ưu hóa lợi nhuận hoặc giảm thiểu chi phí.
5. Làm sao để cải thiện kỹ năng giải và biện luận hệ bất phương trình?
Để cải thiện kỹ năng giải và biện luận hệ bất phương trình, bạn cần luyện tập thường xuyên, tìm hiểu thêm các tài liệu tham khảo và tham gia các lớp học bổ trợ.
Gợi ý các bài viết khác
- Bài tập giải tích a4
- Bài tập lý thuyết kế toán có lời giải
- App giải toán học sinh lớp 3 trên pc
- Rubik tự giải
- Giải toán lớp 8 tập 1
Kêu gọi hành động
Hãy thử giải một vài hệ bất phương trình và xem bạn có thể chiến thắng được thử thách này không! Nếu gặp khó khăn, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ. Chúng tôi có đội ngũ chuyên gia sẵn sàng giúp bạn chinh phục mọi thử thách trong lĩnh vực toán học.
Liên hệ với chúng tôi:
- Số Điện Thoại: 02033846993
- Email: giaibongda@gmail.com
- Địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam
Chúng tôi luôn sẵn sàng phục vụ bạn 24/7!
