Giải Toán Lớp 9 Học Kì 2 là một trong những giai đoạn quan trọng giúp học sinh chuẩn bị tốt cho kì thi vào lớp 10. Học kì này tập trung vào các kiến thức trọng tâm như hệ phương trình, phương trình bậc hai, hàm số bậc hai và hình học. Nắm vững các kiến thức này không chỉ giúp học sinh đạt điểm cao trong các bài kiểm tra mà còn tạo nền tảng vững chắc cho việc học tập ở các cấp học cao hơn. Bạn đang tìm kiếm tài liệu ôn tập cho giải toán lớp 9 học kì 2? Bài viết này sẽ cung cấp cho bạn những kiến thức cần thiết và mẹo làm bài hiệu quả. Hãy cùng khám phá!
Hệ Phương Trình
Hệ phương trình là một phần quan trọng trong chương trình giải toán lớp 9 học kì 2. Học sinh cần nắm vững các phương pháp giải hệ phương trình như phương pháp thế, phương pháp cộng đại số và phương pháp đặt ẩn phụ. Việc luyện tập thường xuyên sẽ giúp học sinh thành thạo các phương pháp này và áp dụng vào giải các bài toán cụ thể. Bạn có thể tham khảo thêm giải bài tập toán lớp 4 trang 27 tập 2 để củng cố kiến thức cơ bản về giải phương trình.
Phương Pháp Thế
Phương pháp thế là một trong những phương pháp cơ bản để giải hệ phương trình. Đầu tiên, ta rút một ẩn từ một phương trình theo ẩn còn lại. Sau đó, thế biểu thức vừa tìm được vào phương trình còn lại để tìm ra giá trị của ẩn.
Phương Pháp Cộng Đại Số
Phương pháp cộng đại số được sử dụng khi các hệ số của cùng một ẩn trong hai phương trình là đối nhau hoặc tỉ lệ với nhau. Ta cộng hoặc trừ hai phương trình để triệt tiêu một ẩn và tìm ra giá trị của ẩn còn lại.
 Giải hệ phương trình lớp 9 học kì 2
Giải hệ phương trình lớp 9 học kì 2
Phương Trình Bậc Hai
Phương trình bậc hai là một dạng toán quan trọng khác trong giải toán lớp 9 học kì 2. Học sinh cần nắm vững công thức nghiệm, định lý Vi-ét và cách vẽ đồ thị hàm số bậc hai. Kiến thức về phương trình bậc hai cũng được ứng dụng rộng rãi trong các bài toán thực tế. Tham khảo thêm giải toán lớp 9 tập 1 bài 1 để nắm vững kiến thức nền tảng.
Công Thức Nghiệm
Công thức nghiệm của phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) là x = (-b ± √Δ) / 2a, trong đó Δ = b² – 4ac.
Định Lý Vi-ét
Định lý Vi-ét cho ta mối quan hệ giữa các nghiệm của phương trình bậc hai với các hệ số a, b, c. Cụ thể, nếu x₁ và x₂ là hai nghiệm của phương trình ax² + bx + c = 0 thì x₁ + x₂ = -b/a và x₁.x₂ = c/a.
Hàm Số Bậc Hai
Hàm số bậc hai có dạng y = ax² + bx + c (a ≠ 0). Đồ thị của hàm số bậc hai là một parabol. Học sinh cần biết cách xác định đỉnh, trục đối xứng và vẽ đồ thị hàm số bậc hai.
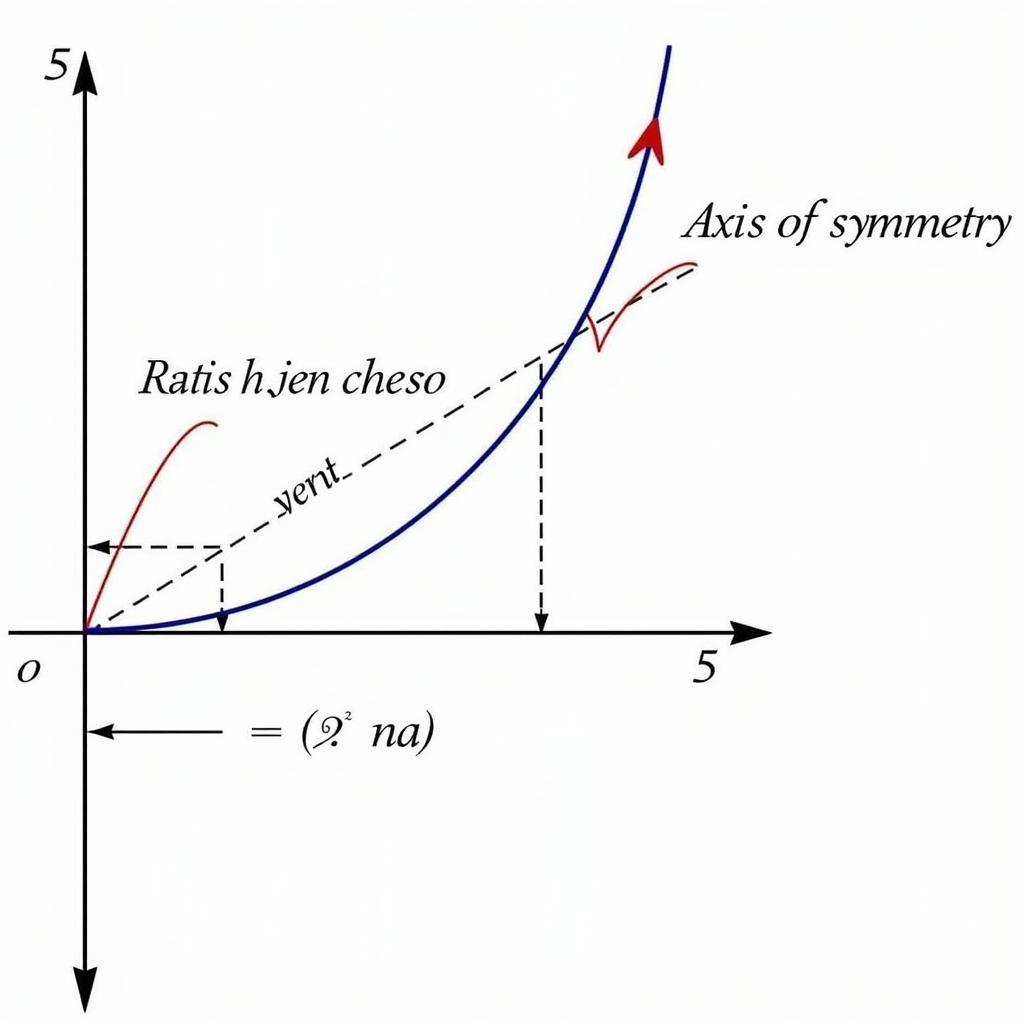 Đồ thị hàm số bậc hai lớp 9
Đồ thị hàm số bậc hai lớp 9
Chuyên gia Nguyễn Văn A, giảng viên Toán tại Đại học Sư phạm Hà Nội, chia sẻ: “Hàm số bậc hai là một kiến thức nền tảng quan trọng, giúp học sinh phát triển tư duy toán học và giải quyết các bài toán ứng dụng.”
Hình Học
Hình học trong giải toán lớp 9 học kì 2 tập trung vào đường tròn, góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung. Học sinh cần nắm vững các định lý và tính chất liên quan để giải các bài toán hình học. Bạn có thể xem thêm giải toán lớp 7 tập 1 bài 2 để ôn lại kiến thức hình học cơ bản.
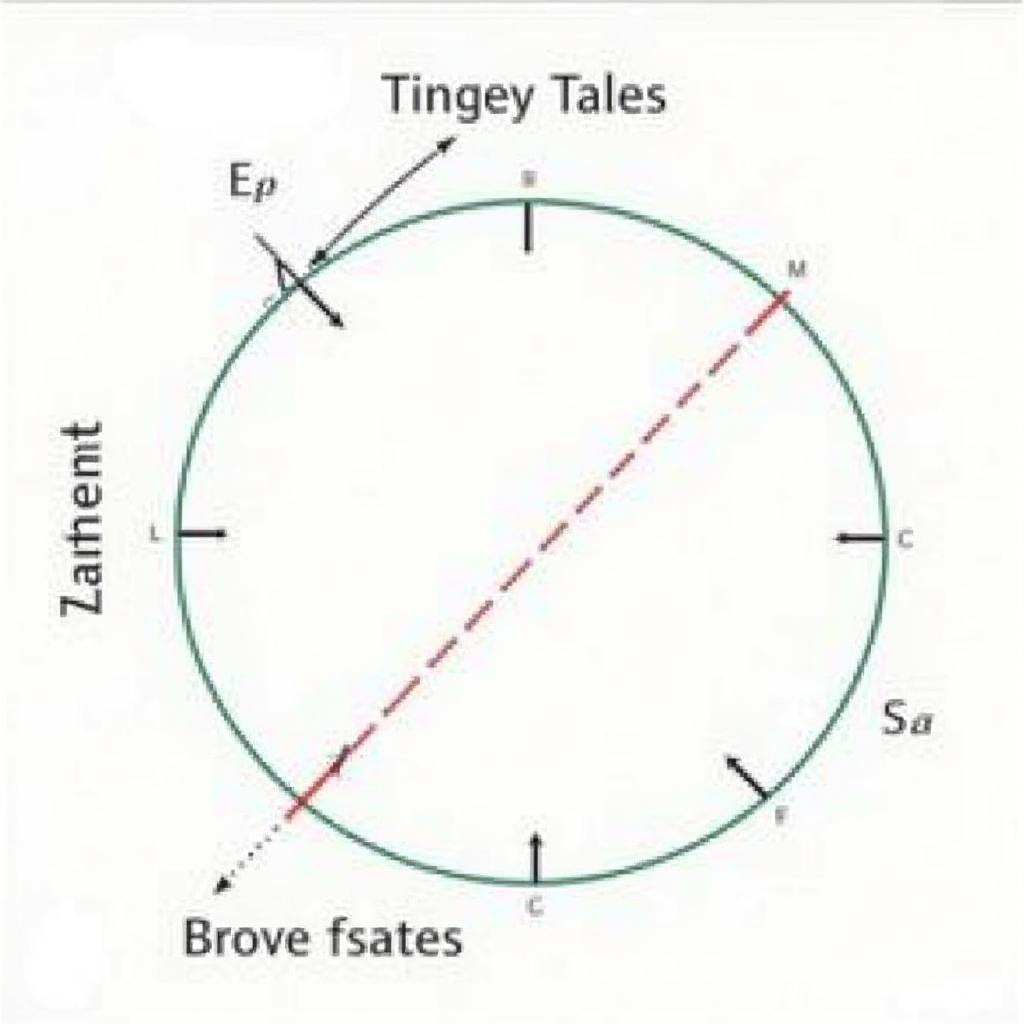 Hình học đường tròn lớp 9
Hình học đường tròn lớp 9
Kết luận
Giải toán lớp 9 học kì 2 đòi hỏi học sinh phải nắm vững các kiến thức trọng tâm như hệ phương trình, phương trình bậc hai, hàm số bậc hai và hình học. Việc ôn tập kỹ lưỡng và luyện tập thường xuyên sẽ giúp học sinh đạt kết quả tốt trong kì thi vào lớp 10. Tài liệu đề thi kế toán máy có lời giải cũng có thể hữu ích cho việc ôn tập.
FAQ
- Làm thế nào để học tốt giải toán lớp 9 học kì 2?
- Phương pháp nào giúp nhớ nhanh công thức nghiệm của phương trình bậc hai?
- Làm sao để vẽ đồ thị hàm số bậc hai chính xác?
- Có những dạng bài hình học nào thường gặp trong kì thi vào lớp 10?
- Làm thế nào để phân biệt các loại góc trong đường tròn?
- Tài liệu nào hữu ích cho việc ôn tập giải toán lớp 9 học kì 2?
- Làm thế nào để áp dụng định lý Vi-ét vào giải bài tập?
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn trong việc vận dụng kiến thức vào giải các bài toán thực tế. Việc làm nhiều bài tập và phân tích các dạng bài sẽ giúp học sinh làm quen và tự tin hơn.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tham khảo thêm các bài viết về giải toán lớp 8 và các đề thi thử vào lớp 10 trên website.
