Giải Toán 12 Nâng Cao là một trong những yếu tố quan trọng giúp học sinh đạt điểm cao trong kỳ thi tốt nghiệp THPT và xét tuyển đại học. Việc nắm vững kiến thức và kỹ năng giải toán 12 nâng cao không chỉ giúp học sinh tự tin khi làm bài thi mà còn rèn luyện tư duy logic, phân tích và giải quyết vấn đề. giải bài tập giải tích 12 nâng cao pdf sẽ giúp bạn rất nhiều trong quá trình ôn luyện.
Phương Pháp Giải Toán 12 Nâng Cao Hiệu Quả
Để giải toán 12 nâng cao hiệu quả, học sinh cần nắm vững các phương pháp giải cơ bản và nâng cao. Việc luyện tập thường xuyên với các dạng bài tập khác nhau sẽ giúp học sinh làm quen với các dạng bài toán và rèn luyện kỹ năng giải quyết vấn đề.
- Nắm vững kiến thức cơ bản: Học sinh cần nắm vững các kiến thức cơ bản của chương trình toán 12, bao gồm các định lý, công thức, tính chất. Đây là nền tảng quan trọng để học sinh có thể tiếp cận và giải quyết các bài toán nâng cao.
- Luyện tập thường xuyên: Việc luyện tập thường xuyên với các dạng bài tập khác nhau sẽ giúp học sinh làm quen với các dạng bài toán và rèn luyện kỹ năng giải quyết vấn đề.
- Phân tích đề bài: Trước khi bắt đầu giải bài toán, học sinh cần đọc kỹ đề bài, phân tích yêu cầu của đề bài và xác định các thông tin đã cho và cần tìm.
- Áp dụng phương pháp phù hợp: Tùy vào từng dạng bài toán, học sinh cần lựa chọn phương pháp giải phù hợp. giải bài tập toán đại 12 nâng cao cung cấp nhiều bài tập và lời giải chi tiết giúp bạn rèn luyện.
 Phân tích đề bài toán 12 nâng cao
Phân tích đề bài toán 12 nâng cao
Giải Toán 12 Nâng Cao: Hàm Số và Ứng Dụng
Hàm số là một trong những chủ đề quan trọng trong chương trình toán 12. Việc nắm vững kiến thức về hàm số sẽ giúp học sinh giải quyết được nhiều bài toán nâng cao liên quan.
Khảo sát hàm số
Khảo sát hàm số là một trong những dạng bài toán thường gặp trong các kỳ thi. Học sinh cần nắm vững các bước khảo sát hàm số để có thể vẽ đồ thị và tìm các điểm đặc biệt của hàm số.
- Tìm tập xác định.
- Tính đạo hàm.
- Xét dấu đạo hàm.
- Tìm cực trị.
- Tìm tiệm cận.
- Vẽ đồ thị.
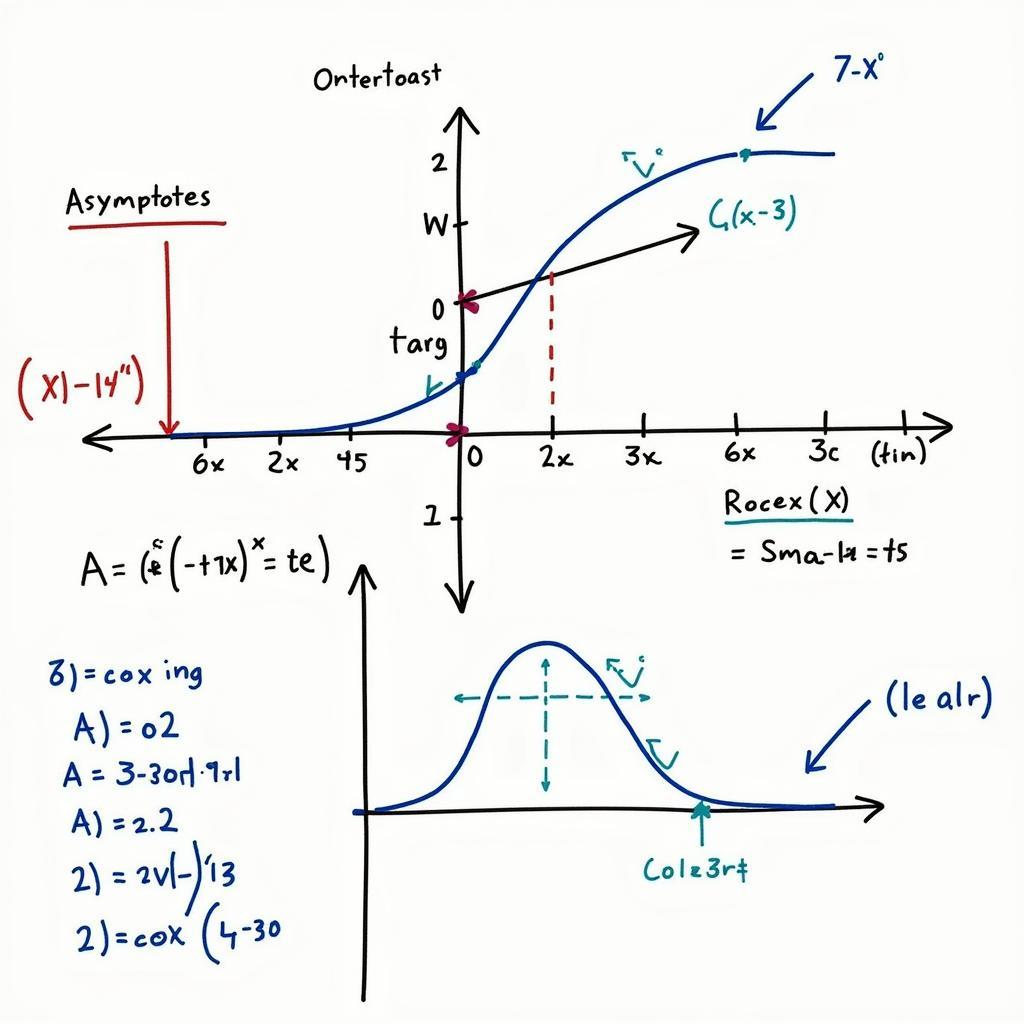 Khảo sát hàm số trong giải toán 12 nâng cao
Khảo sát hàm số trong giải toán 12 nâng cao
Ứng dụng của đạo hàm
Đạo hàm có nhiều ứng dụng trong giải toán 12 nâng cao, ví dụ như tìm giá trị lớn nhất, nhỏ nhất của hàm số, giải bài toán liên quan đến vận tốc, gia tốc… Bạn có thể tham khảo thêm giải sbt toán 12 nâng cao.
Ông Nguyễn Văn A, giáo viên Toán trường THPT XYZ, chia sẻ: “Việc luyện tập thường xuyên với các bài toán nâng cao sẽ giúp học sinh rèn luyện tư duy logic và kỹ năng giải quyết vấn đề, từ đó đạt kết quả cao trong kỳ thi.”
Giải Toán 12 Nâng Cao: Hình Học Không Gian
Hình học không gian cũng là một phần quan trọng trong chương trình toán 12. Học sinh cần nắm vững các công thức tính thể tích, diện tích các hình khối trong không gian.
 Hình học không gian trong giải toán 12 nâng cao
Hình học không gian trong giải toán 12 nâng cao
Bà Trần Thị B, giảng viên Đại học ABC, cho biết: “Hình học không gian yêu cầu học sinh có khả năng tư duy hình học tốt. Việc sử dụng hình vẽ minh họa sẽ giúp học sinh dễ dàng hình dung và giải quyết bài toán.”
Kết luận
Giải toán 12 nâng cao là một quá trình đòi hỏi sự kiên trì và nỗ lực. Học sinh cần nắm vững kiến thức cơ bản, luyện tập thường xuyên và áp dụng các phương pháp giải toán phù hợp để đạt được kết quả tốt trong kỳ thi. bài 3.1 sbt toán 12 giải tích nâng cao là một ví dụ điển hình về bài tập nâng cao. Chúc các bạn thành công!
FAQ
- Làm thế nào để học tốt giải toán 12 nâng cao?
- Tài liệu nào hữu ích cho việc ôn tập giải toán 12 nâng cao?
- Các dạng bài toán nào thường gặp trong đề thi đại học?
- Làm sao để khắc phục những điểm yếu trong giải toán 12 nâng cao?
- Có nên học thêm toán 12 nâng cao không?
- Làm thế nào để phân bổ thời gian học toán 12 nâng cao hiệu quả?
- Kỹ năng nào quan trọng nhất khi giải toán 12 nâng cao?
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn với các bài toán liên quan đến khảo sát hàm số, ứng dụng đạo hàm, hình học không gian. Việc tìm kiếm lời giải chi tiết và bài tập tương tự sẽ giúp học sinh hiểu rõ hơn về cách giải quyết các dạng bài toán này.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tham khảo thêm các bài viết về giải sbt vật lí 7 bài 13.
