Phương trình lượng giác sin 2x = 1 là một dạng bài toán cơ bản thường gặp trong chương trình toán học phổ thông. Bài viết này sẽ hướng dẫn chi tiết cách giải pt sin 2x = 1, cùng với những ví dụ minh họa và phân tích sâu về bản chất của phương trình này. Ngay sau đây, chúng ta sẽ cùng nhau khám phá cách giải quyết bài toán này một cách hiệu quả.
Phương trình sin 2x = 1 thuộc dạng phương trình lượng giác cơ bản. Để giải phương trình này, ta cần tìm giá trị của x sao cho sin của góc 2x bằng 1. Việc nắm vững đường tròn lượng giác và các giá trị đặc biệt của hàm sin sẽ giúp chúng ta dễ dàng giải quyết bài toán này. Bạn có thể tham khảo thêm về cách giải phương trình bậc 2 tại cach giải pt bậc 2.
Giải phương trình sin 2x = 1: Hướng dẫn từng bước
Để giải phương trình sin 2x = 1, ta thực hiện theo các bước sau:
- Xác định góc có sin bằng 1: Trên đường tròn lượng giác, sin của góc bằng 1 tại góc π/2 (90 độ).
- Biểu diễn nghiệm tổng quát: Vì hàm sin tuần hoàn với chu kỳ 2π, nên nghiệm tổng quát của phương trình sin 2x = 1 sẽ là: 2x = π/2 + k2π, với k là số nguyên.
- Rút gọn nghiệm: Chia cả hai vế cho 2, ta được: x = π/4 + kπ, với k là số nguyên.
Ví dụ minh họa giải pt sin 2x = 1
Ví dụ 1: Tìm tất cả các nghiệm của phương trình sin 2x = 1 trong khoảng [0, 2π].
- Giải: Dựa vào nghiệm tổng quát x = π/4 + kπ, ta thay các giá trị của k để tìm nghiệm trong khoảng đã cho.
- Với k = 0, x = π/4.
- Với k = 1, x = 5π/4.
- Với k = 2, x = 9π/4 (không thuộc khoảng [0, 2π]).
Vậy, các nghiệm của phương trình trong khoảng [0, 2π] là π/4 và 5π/4.
Ví dụ 2: Giải phương trình sin 2x = 1 và biểu diễn nghiệm trên đường tròn lượng giác.
- Giải: Nghiệm tổng quát là x = π/4 + kπ. Trên đường tròn lượng giác, các nghiệm này tương ứng với các điểm nằm trên đường tròn tại góc π/4 và 5π/4.
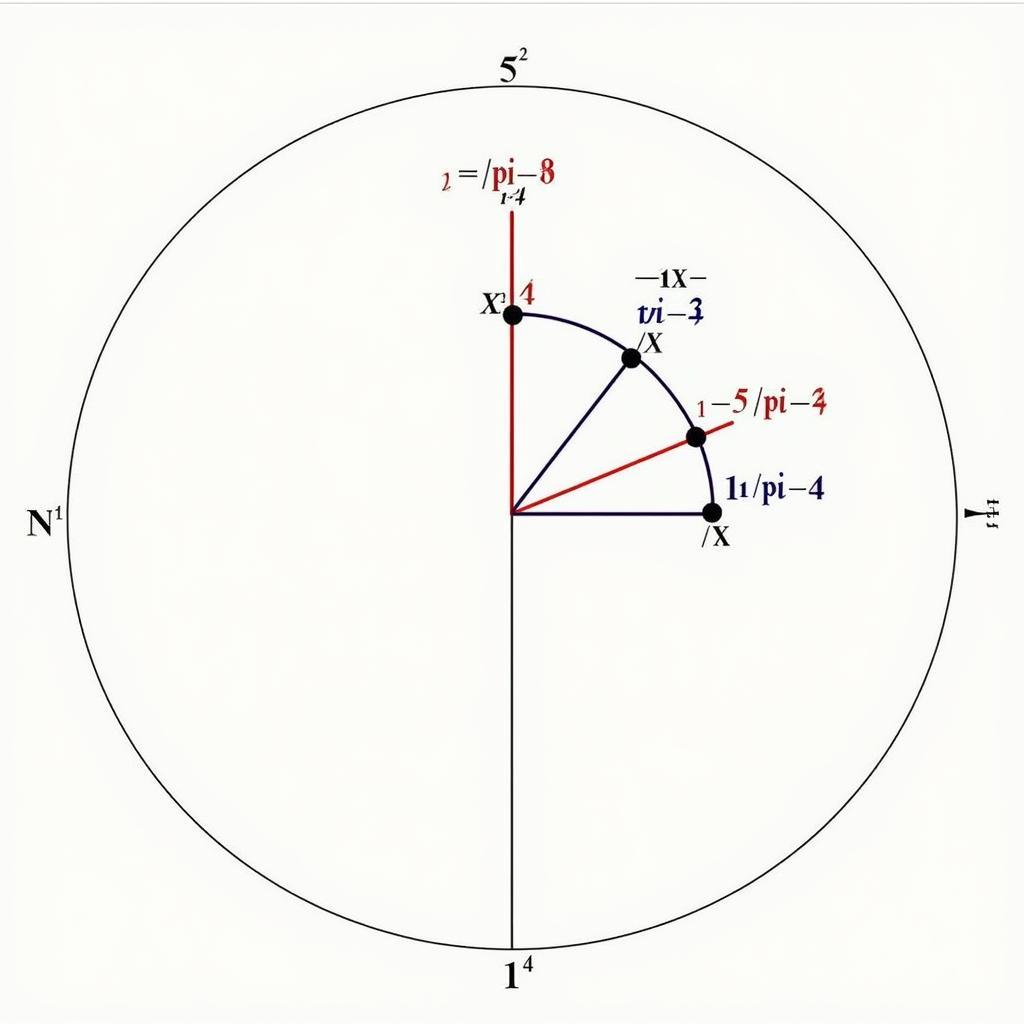Giải pt sin 2x = 1 trên đường tròn lượng giác
Bạn có thể tìm hiểu thêm về giải phương trình lớp 9 tại giải phương trình lớp 9.
Ứng dụng của phương trình sin 2x = 1
Phương trình sin 2x = 1, mặc dù đơn giản, nhưng lại có ứng dụng trong nhiều lĩnh vực, đặc biệt là trong vật lý và kỹ thuật, khi mô tả các hiện tượng dao động và sóng.
Chuyên gia Nguyễn Văn A – Giảng viên Toán học Đại học Khoa học Tự nhiên: “Phương trình lượng giác, đặc biệt là dạng phương trình sin 2x = 1, là nền tảng để hiểu và giải quyết các bài toán phức tạp hơn trong toán học và các ngành khoa học ứng dụng.”
Khi nào sin 2x = 1?
Sin 2x = 1 khi góc 2x có giá trị bằng π/2 cộng với bội số nguyên của 2π. Điều này xảy ra khi x = π/4 + kπ, với k là số nguyên. Nắm vững kiến thức về bài tập về khoảng cách lớp 11 có lời giải có thể hỗ trợ bạn rất nhiều trong việc hình dung và giải quyết các bài toán lượng giác. Bạn có thể tìm thấy tài liệu hữu ích tại bài tập về khoảng cách lớp 11 có lời giải.
Giải phương trình sin 2x = 1 bằng máy tính
Việc sử dụng máy tính, ví dụ như Vinacal, có thể giúp kiểm tra nghiệm của phương trình. Tham khảo thêm về cách sử dụng máy tính để giải hệ phương trình tại bấm máy tính giải hệ phương trình vinacal.
Chuyên gia Trần Thị B – Giáo viên Toán THPT Chuyên Hà Nội – Amsterdam: “Việc sử dụng máy tính cầm tay là một công cụ hỗ trợ hữu ích, giúp học sinh kiểm tra lại kết quả và tiết kiệm thời gian khi giải các phương trình lượng giác.”
Kết luận
Bài viết đã trình bày chi tiết cách giải pt sin 2x = 1, từ việc xác định nghiệm tổng quát đến các ví dụ minh họa cụ thể. Hiểu rõ phương pháp giải phương trình này sẽ giúp bạn nắm vững kiến thức lượng giác cơ bản và ứng dụng vào các bài toán phức tạp hơn.
Giải pt sin 2x = 1 ứng dụng thực tế
FAQ
- Nghiệm tổng quát của phương trình sin 2x = 1 là gì?
- x = π/4 + kπ, với k là số nguyên.
- Làm thế nào để tìm nghiệm của sin 2x = 1 trong một khoảng cho trước?
- Thay các giá trị nguyên của k vào nghiệm tổng quát để tìm các nghiệm thuộc khoảng đó.
- Phương trình sin 2x = 1 có bao nhiêu nghiệm?
- Phương trình này có vô số nghiệm do tính tuần hoàn của hàm sin.
- Ứng dụng của phương trình sin 2x = 1 trong thực tế là gì?
- Ứng dụng trong mô tả các hiện tượng dao động và sóng trong vật lý và kỹ thuật.
- Làm thế nào để biểu diễn nghiệm của sin 2x = 1 trên đường tròn lượng giác?
- Biểu diễn các góc x = π/4 + kπ trên đường tròn.
- Có thể giải sin 2x = 1 bằng máy tính không?
- Có, có thể sử dụng máy tính để kiểm tra nghiệm.
- Sin 2x bằng 1 khi nào?
- Khi 2x = π/2 + k2π, hay x = π/4 + kπ (k là số nguyên).
Bạn cũng có thể tham khảo thêm về giải bất phương trình chứa giá trị tuyệt đối trên trang web của chúng tôi.
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.