Giải PT Bậc Nhất C++: Hướng Dẫn Chi Tiết

Puskasvào
Ví dụ code C++ giải phương trình bậc nhất

Giải Pt Bậc Nhất C++ là một kỹ năng lập trình cơ bản, cần thiết cho bất kỳ ai muốn theo đuổi sự nghiệp trong lĩnh vực công nghệ thông tin. Bài viết này sẽ cung cấp cho bạn hướng dẫn chi tiết về cách giải phương trình bậc nhất bằng ngôn ngữ C++, từ những khái niệm cơ bản đến các ví dụ thực tế. Bạn sẽ tìm hiểu cách viết mã để giải phương trình bậc nhất một ẩn và áp dụng nó vào các bài toán cụ thể. Ngay sau đoạn mở đầu này, chúng ta sẽ đi sâu vào chi tiết. Xem thêm về cách giải pt bậc nhất 2 ẩn.

Giải Phương Trình Bậc Nhất: Khái Niệm Cơ Bản

Phương trình bậc nhất một ẩn có dạng ax + b = 0, với a và b là các hằng số và a khác 0. Mục tiêu của chúng ta là tìm giá trị của x thỏa mãn phương trình. Công thức nghiệm tổng quát là x = -b/a.

Giải PT Bậc Nhất C++: Hướng Dẫn Từng Bước

Để giải pt bậc nhất C++, chúng ta cần thực hiện các bước sau:

  1. Khai báo thư viện: Bắt đầu bằng việc khai báo thư viện iostream để sử dụng các hàm nhập xuất như cin và cout.
  2. Khai báo biến: Khai báo các biến a, b, và x kiểu dữ liệu float hoặc double để lưu trữ các hệ số và nghiệm.
  3. Nhập dữ liệu: Sử dụng cin để nhập giá trị cho a và b từ người dùng.
  4. Kiểm tra điều kiện: Kiểm tra xem a có bằng 0 hay không. Nếu a bằng 0, phương trình không phải là bậc nhất.
  5. Tính nghiệm: Nếu a khác 0, tính nghiệm x theo công thức x = -b/a.
  6. Xuất kết quả: Sử dụng cout để hiển thị giá trị của x ra màn hình.

Ví Dụ Giải PT Bậc Nhất C++

#include <iostream>

using namespace std;

int main() {
    float a, b, x;

    cout << "Nhap he so a: ";
    cin >> a;

    cout << "Nhap he so b: ";
    cin >> b;

    if (a == 0) {
        if (b == 0) {
            cout << "Phuong trinh vo so nghiem." << endl;
        } else {
            cout << "Phuong trinh vo nghiem." << endl;
        }
    } else {
        x = -b / a;
        cout << "Nghiem cua phuong trinh la x = " << x << endl;
    }

    return 0;
}

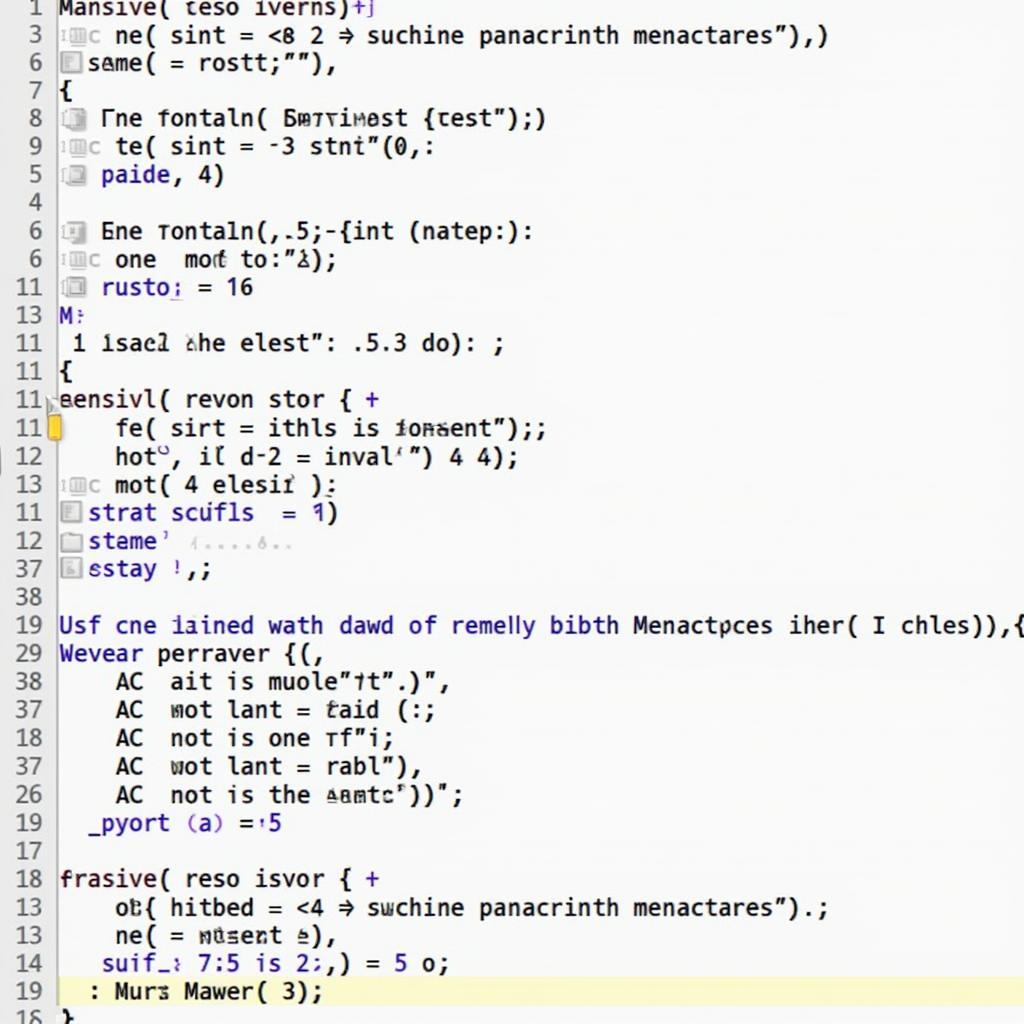Ví dụ code C++ giải phương trình bậc nhấtVí dụ code C++ giải phương trình bậc nhất

Giải PT Bậc Nhất C++: Xử Lý Trường Hợp Đặc Biệt

Khi a bằng 0, phương trình trở thành b = 0. Nếu b cũng bằng 0, phương trình có vô số nghiệm. Nếu b khác 0, phương trình vô nghiệm. Cần xử lý các trường hợp này trong mã C++ để tránh lỗi. Tham khảo thêm về bài tập giải phuong trình đệ quy.

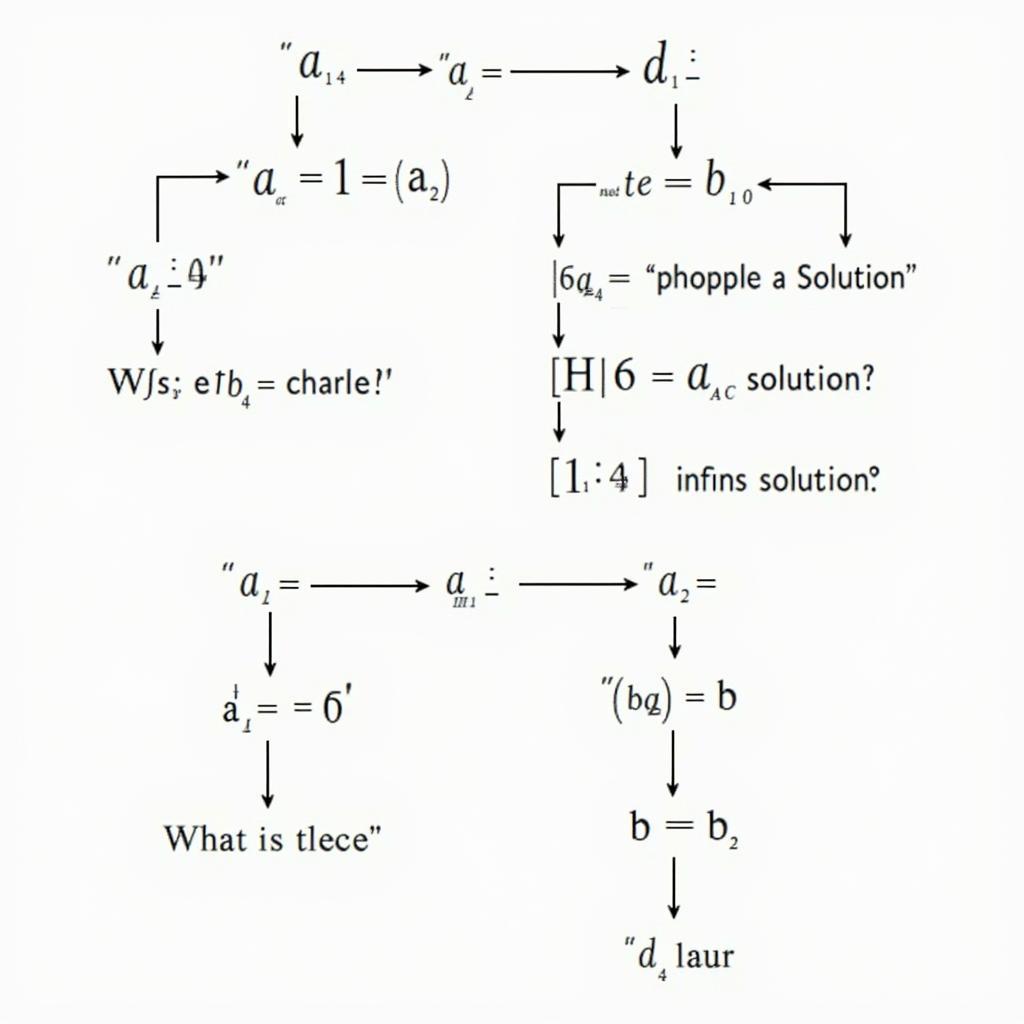Sơ đồ xử lý trường hợp đặc biệt khi a=0Sơ đồ xử lý trường hợp đặc biệt khi a=0

Giải PT Bậc Nhất Trong Thực Tế

Giải pt bậc nhất C++ không chỉ là một bài tập lập trình đơn giản. Nó có ứng dụng rộng rãi trong nhiều lĩnh vực, từ tính toán vật lý đến xử lý dữ liệu. Ví dụ, bạn có thể sử dụng nó để tính toán tốc độ, quãng đường, hoặc thời gian trong các bài toán vật lý. Tìm hiểu thêm về giải hệ pt.

Nguyễn Văn A, một chuyên gia lập trình C++ tại Việt Nam, cho biết: “Việc nắm vững cách giải pt bậc nhất C++ là nền tảng quan trọng cho việc học các thuật toán phức tạp hơn.”

Kết Luận

Giải pt bậc nhất C++ là một kỹ năng cơ bản nhưng rất quan trọng. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết để giải quyết các bài toán liên quan đến phương trình bậc nhất. Hãy luyện tập thường xuyên để nâng cao kỹ năng lập trình của bạn. Bên cạnh đó, việc tìm hiểu thêm về bài toán lớp 9 giải hệ phương trunhf cũng rất hữu ích.

Trần Thị B, giảng viên đại học chuyên ngành Công nghệ thông tin, chia sẻ: “Giải pt bậc nhất C++ là bước khởi đầu cho việc học lập trình. Nó giúp sinh viên làm quen với cú pháp và tư duy lập trình.”

FAQ

  1. Cần khai báo thư viện nào để giải pt bậc nhất C++? Bạn cần khai báo thư viện iostream.
  2. Công thức nghiệm của phương trình bậc nhất là gì? Công thức là x = -b/a.
  3. Làm thế nào để xử lý trường hợp a = 0? Kiểm tra giá trị của b. Nếu b cũng bằng 0, phương trình có vô số nghiệm. Nếu b khác 0, phương trình vô nghiệm.
  4. Ứng dụng của giải pt bậc nhất trong thực tế là gì? Ứng dụng trong tính toán vật lý, xử lý dữ liệu, và nhiều lĩnh vực khác.
  5. Kiểu dữ liệu nào nên dùng cho biến a, b, và x? Nên dùng float hoặc double.
  6. Tại sao cần kiểm tra a khác 0? Vì nếu a = 0, phương trình không phải là bậc nhất.
  7. Làm thế nào để nhập dữ liệu từ người dùng? Sử dụng cin.

Mô tả các tình huống thường gặp câu hỏi.

Người dùng thường gặp khó khăn khi xử lý trường hợp a=0. Cần lưu ý kiểm tra giá trị của b để đưa ra kết luận chính xác về nghiệm của phương trình.

Gợi ý các câu hỏi khác, bài viết khác có trong web.

Bạn có thể tìm hiểu thêm về cách giải phẫu da đầu.