Giải Hình Học là một phần quan trọng trong toán học, giúp chúng ta hiểu rõ hơn về các hình dạng, kích thước và mối quan hệ giữa các đối tượng trong không gian. Từ những khái niệm cơ bản về điểm, đường thẳng, đến các hình phức tạp hơn như hình tròn, hình vuông, hình cầu, giải hình học cung cấp cho chúng ta những công cụ để phân tích và giải quyết các bài toán thực tế.
Bạn đã bao giờ tự hỏi làm thế nào các kiến trúc sư thiết kế những tòa nhà cao tầng vững chắc, hay làm thế nào các kỹ sư tính toán quỹ đạo của một vệ tinh? Giải hình học chính là nền tảng cho những thành tựu đó. Nắm vững các nguyên tắc của giải hình học không chỉ giúp bạn đạt điểm cao trong các bài kiểm tra toán học mà còn phát triển tư duy logic và khả năng giải quyết vấn đề. Tham khảo thêm bài tập toán hình học lớp 8 có lời giải.
Khám Phá Các Định Lý Cơ Bản Trong Giải Hình Học
Các định lý cơ bản trong giải hình học, như định lý Pythagore, định lý Thales, là những viên gạch nền tảng để xây dựng nên toàn bộ kiến thức về hình học. Hiểu rõ và áp dụng thành thạo các định lý này là chìa khóa để giải quyết các bài toán hình học phức tạp.
Định Lý Pythagore: Mối Quan Hệ Giữa Các Cạnh Trong Tam Giác Vuông
Định lý Pythagore phát biểu rằng trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Đây là một trong những định lý quan trọng nhất trong giải hình học, được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau.
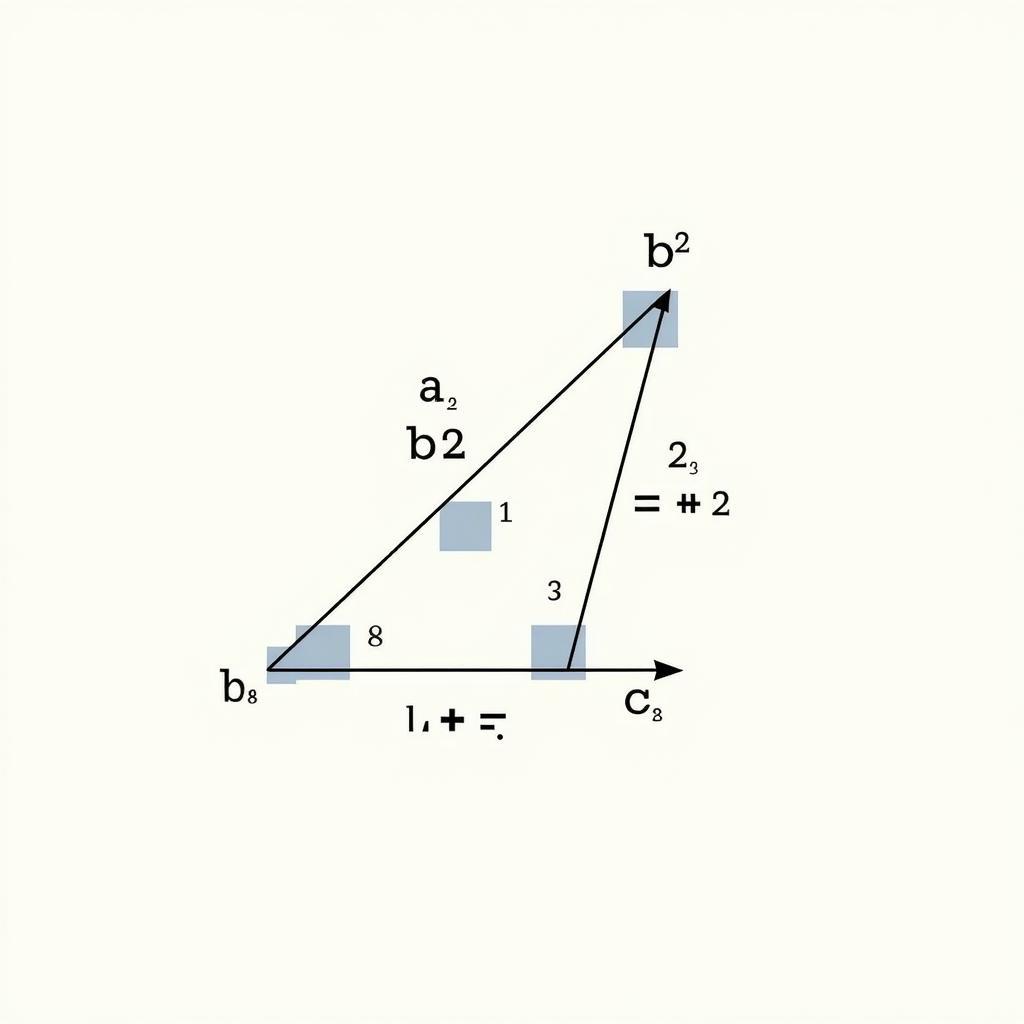Minh họa Định Lý Pythagore trong tam giác vuông
Định Lý Thales: Tỷ Lệ Giữa Các Đoạn Thẳng
Định lý Thales liên quan đến tỷ lệ giữa các đoạn thẳng được tạo bởi các đường thẳng song song cắt hai đường thẳng khác. Định lý này có nhiều ứng dụng trong việc chứng minh các tính chất của hình học phẳng.
Giải Hình Học Trong Không Gian
Giải hình học không chỉ giới hạn ở mặt phẳng mà còn mở rộng ra không gian ba chiều. Chúng ta sẽ tìm hiểu về các hình khối như hình hộp, hình cầu, hình chóp, và các mối quan hệ giữa chúng. Việc hình dung và phân tích các hình khối trong không gian đòi hỏi tư duy trừu tượng và khả năng quan sát tốt. Xem thêm bài tập cơ học kết cấu 1 có lợi giải.
Hình dung hình khối trong không gian 3 chiều
Việc hình dung các hình khối trong không gian ba chiều là một kỹ năng quan trọng trong giải hình học. Có nhiều phương pháp giúp bạn rèn luyện kỹ năng này, chẳng hạn như sử dụng các mô hình vật lý, vẽ hình chiếu, hoặc sử dụng phần mềm đồ họa.
Giáo sư Nguyễn Văn A, chuyên gia hàng đầu về hình học tại Đại học Quốc gia Hà Nội, cho biết: “Việc nắm vững giải hình học không chỉ giúp học sinh giải toán tốt hơn mà còn phát triển tư duy logic và khả năng giải quyết vấn đề.”
Ứng Dụng Của Giải Hình Học Trong Đời Sống
Giải hình học có vô số ứng dụng trong đời sống, từ việc thiết kế nhà cửa, cầu đường, đến việc đo đạc đất đai, vẽ bản đồ. Nó cũng là nền tảng cho nhiều ngành khoa học khác như vật lý, thiên văn học, và khoa học máy tính. Có thể bạn quan tâm đến giải đấu.
Giải hình học trong kiến trúc và xây dựng
Trong kiến trúc và xây dựng, giải hình học được sử dụng để tính toán diện tích, thể tích, và thiết kế các cấu trúc vững chắc. Kiến thức về hình học là không thể thiếu đối với các kiến trúc sư và kỹ sư xây dựng.
Tiến sĩ Trần Thị B, một kiến trúc sư giàu kinh nghiệm, chia sẻ: “Giải hình học là công cụ không thể thiếu trong công việc của tôi. Nó giúp tôi thiết kế những công trình vừa đẹp mắt vừa an toàn.” Tham khảo bài giải toán 8 tập 1 hình học mua sách và giải bài tập địa lí lớp 7.
Kết luận
Giải hình học là một phần quan trọng của toán học, có ứng dụng rộng rãi trong đời sống. Nắm vững kiến thức về giải hình học không chỉ giúp chúng ta giải quyết các bài toán mà còn phát triển tư duy logic và khả năng quan sát.
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.