Giải Hệ Bất Phương Trình 2 Ẩn: Phương Pháp và Bài Tập Minh Họa

Giải hệ bất phương trình 2 ẩn là một dạng toán quan trọng trong chương trình Toán lớp 10. Bài viết này sẽ cung cấp cho bạn cái nhìn tổng quan về phương pháp giải hệ bất phương trình 2 ẩn, kèm theo các bài tập minh họa để bạn nắm vững kiến thức.

Phương Pháp Biểu Diễn Hình Học

Phương pháp biểu diễn hình học là cách tiếp cận trực quan và dễ hiểu nhất để giải quyết hệ bất phương trình 2 ẩn.

Bước 1: Biểu Diễn Miền Nghiệm của Từng Bất Phương Trình

Vẽ đường thẳng biểu diễn cho phương trình tương ứng của mỗi bất phương trình.
Lấy một điểm bất kỳ không thuộc đường thẳng, thường là (0,0), để thử nghiệm.
Nếu điểm thử nghiệm thỏa mãn bất phương trình, miền nghiệm sẽ là phần mặt phẳng chứa điểm đó và bị giới hạn bởi đường thẳng. Ngược lại, miền nghiệm sẽ là phần mặt phẳng không chứa điểm thử nghiệm.

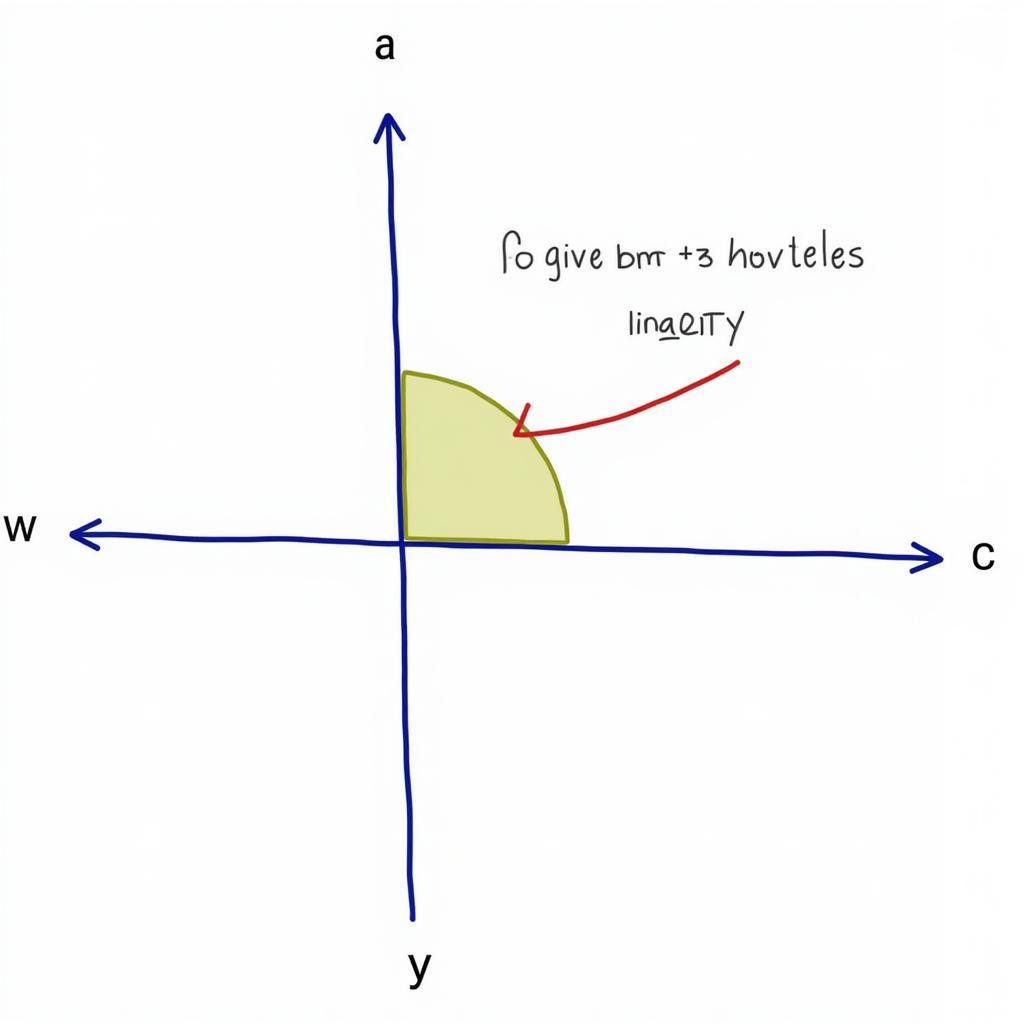Miền Nghiệm của Bất Phương Trình

Bước 2: Xác Định Miền Nghiệm Chung

Miền nghiệm chung của hệ bất phương trình là phần mặt phẳng giao nhau của tất cả các miền nghiệm đã biểu diễn ở bước 1.

Miền Nghiệm Chung

Ví Dụ Minh Họa

Giải hệ bất phương trình:

x + y ≤ 4 
2x - y ≥ 0

Bước 1: Biểu diễn miền nghiệm của từng bất phương trình:

Bất phương trình x + y ≤ 4: Đường thẳng x + y = 4 đi qua hai điểm (0,4) và (4,0). Thử nghiệm với điểm (0,0), ta có 0 + 0 ≤ 4 (đúng). Vậy, miền nghiệm là phần mặt phẳng chứa điểm (0,0) và bị giới hạn bởi đường thẳng x + y = 4.
Bất phương trình 2x - y ≥ 0: Đường thẳng 2x - y = 0 đi qua hai điểm (0,0) và (1,2). Thử nghiệm với điểm (1,0), ta có 2 * 1 – 0 ≥ 0 (đúng). Vậy, miền nghiệm là phần mặt phẳng chứa điểm (1,0) và bị giới hạn bởi đường thẳng 2x - y = 0.

Bước 2: Miền nghiệm chung của hệ bất phương trình là phần mặt phẳng giao nhau của hai miền nghiệm đã biểu diễn, được giới hạn bởi đường thẳng x + y = 4 và 2x - y = 0.

Giải Hệ Bất Phương Trình

Ứng Dụng của Hệ Bất Phương Trình 2 Ẩn

Giải hệ bất phương trình 2 ẩn không chỉ là một bài toán trừu tượng mà còn có rất nhiều ứng dụng trong thực tế, đặc biệt là trong lĩnh vực kinh tế và tối ưu hóa.

giải bài tập tiếng việt lớp 2

Bài Tập Vận Dụng

Giải các hệ bất phương trình sau:

```
x - y + 2 > 0
x + y - 2 ≤ 0
```
```
2x + 3y ≤ 6
x - 2y ≥ 4
```

Kết Luận

Bài viết đã cung cấp cho bạn phương pháp giải hệ bất phương trình 2 ẩn bằng cách biểu diễn hình học, kèm theo các ví dụ minh họa chi tiết. Hy vọng rằng, bài viết này sẽ giúp bạn tự tin hơn khi giải quyết dạng toán này.