Giải Bất Phương Trình Lớp 9 là một trong những kiến thức quan trọng, là nền tảng vững chắc cho các bài toán nâng cao ở bậc học cao hơn. Bài viết này sẽ cung cấp cho bạn những phương pháp giải bất phương trình lớp 9 hiệu quả, kèm theo các ví dụ minh họa và bài tập vận dụng để bạn nắm vững kiến thức.
Các Phương Pháp Giải Bất Phương Trình Lớp 9
1. Phương pháp biến đổi tương đương
Đây là phương pháp phổ biến nhất để giải bất phương trình lớp 9. Nguyên tắc của phương pháp này là dùng các phép biến đổi tương đương để đưa bất phương trình ban đầu về bất phương trình đơn giản hơn, từ đó tìm ra tập nghiệm.
Các phép biến đổi tương đương thường dùng:
- Cộng (trừ) cả hai vế của bất phương trình với cùng một số hoặc một biểu thức.
- Nhân (chia) cả hai vế của bất phương trình với cùng một số dương.
- Nhân (chia) cả hai vế của bất phương trình với cùng một số âm và đổi chiều bất đẳng thức.
Ví dụ: Giải bất phương trình: 2x + 3 > 7
Giải:
2x + 3 > 7
<=> 2x > 4
<=> x > 2Vậy tập nghiệm của bất phương trình là S = {x | x > 2}
2. Phương pháp sử dụng đồ thị
Phương pháp này thường được áp dụng để giải các bất phương trình bậc nhất hai ẩn. Ta biểu diễn miền nghiệm của bất phương trình trên mặt phẳng tọa độ Oxy.
Các bước thực hiện:
- Biến đổi bất phương trình về dạng ax + by + c > 0 (hoặc < 0, ≥ 0, ≤ 0).
- Vẽ đường thẳng (d): ax + by + c = 0.
- Lấy một điểm M(x0; y0) không thuộc đường thẳng (d).
- Thay tọa độ điểm M vào bất phương trình.
- Nếu bất phương trình đúng, miền nghiệm là nửa mặt phẳng bờ (d) chứa điểm M.
- Nếu bất phương trình sai, miền nghiệm là nửa mặt phẳng bờ (d) không chứa điểm M.
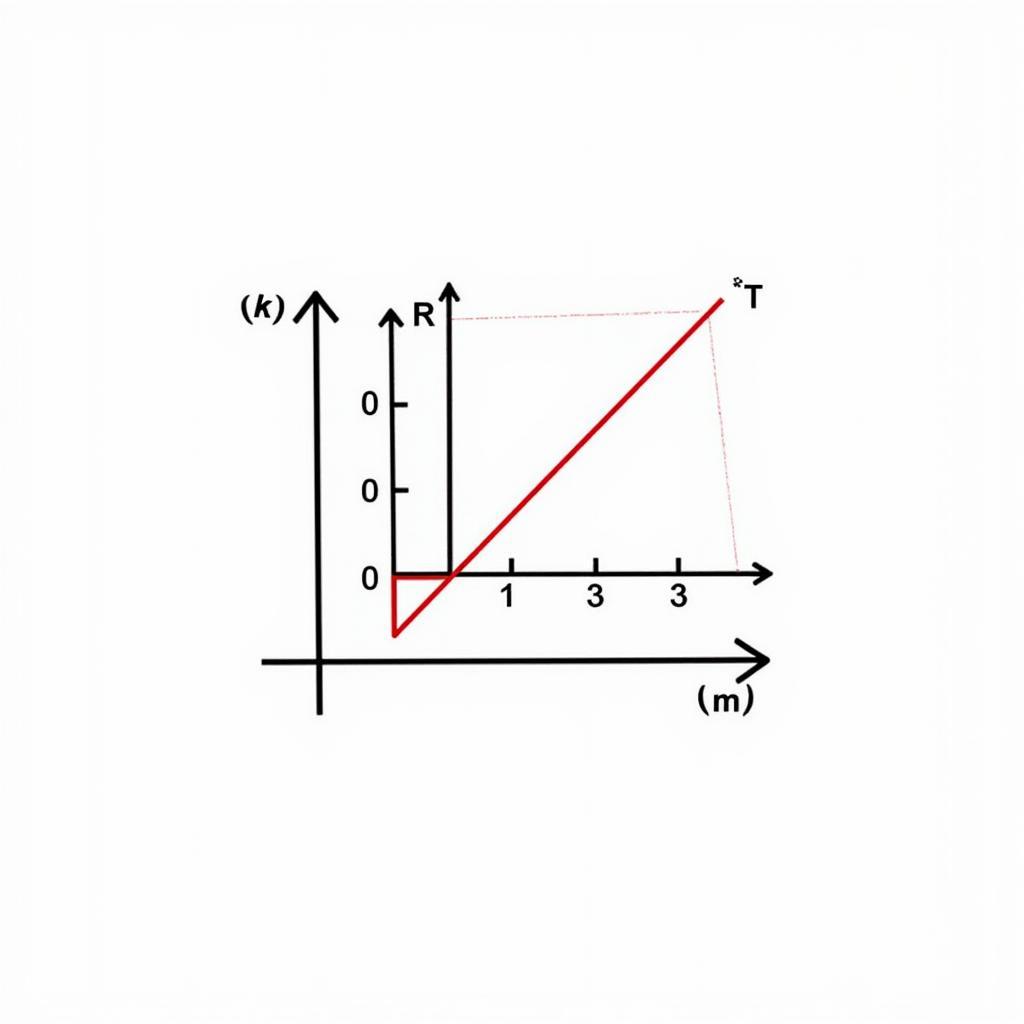Giải bất phương trình bằng đồ thị
Ví dụ: Giải bất phương trình: x + y – 2 > 0
Giải:
- Vẽ đường thẳng (d): x + y – 2 = 0.
- Lấy điểm M(0; 0) ∉ (d).
- Thay x = 0, y = 0 vào bất phương trình ta được: 0 + 0 – 2 = -2 < 0.
- Vậy miền nghiệm là nửa mặt phẳng bờ (d) không chứa điểm M (0; 0).
3. Phương pháp xét dấu nhị thức bậc nhất
Phương pháp này thường được áp dụng để giải các bất phương trình chứa dấu giá trị tuyệt đối, bất phương trình tích, bất phương trình thương.
Các bước thực hiện:
- Tìm nghiệm của các nhị thức bậc nhất có trong bất phương trình.
- Lập bảng xét dấu của các nhị thức bậc nhất.
- Dựa vào bảng xét dấu, tìm ra các khoảng nghiệm của bất phương trình.
Ví dụ: Giải bất phương trình: (x – 1)(x + 2) < 0
Giải:
- Nghiệm của x – 1 = 0 là x = 1.
- Nghiệm của x + 2 = 0 là x = -2.
- Lập bảng xét dấu:
| x | -∞ | -2 | 1 | +∞ |
|---|---|---|---|---|
| x-1 | – | – | + | + |
| x+2 | – | + | + | + |
| f(x) | + | – | + | + |
- Vậy tập nghiệm của bất phương trình là S = {x | -2 < x < 1}.
Bài Tập Vận Dụng
Bài 1: Giải bất phương trình: 3(x – 2) + 5 < 2x + 7
Bài 2: Giải bất phương trình: |x – 3| ≤ 2
Bài 3: Giải bất phương trình: (x + 1)(x – 4) ≥ 0
Giải bất phương trình bậc nhất
Mẹo Giải Nhanh Bất Phương Trình Lớp 9
- Nắm vững kiến thức cơ bản: Nắm vững các định nghĩa, tính chất, các phép biến đổi tương đương… là điều kiện tiên quyết để giải bất phương trình một cách hiệu quả.
- Luyện tập thường xuyên: Luyện giải nhiều dạng bài tập khác nhau giúp bạn nhanh chóng nhận dạng dạng bài và áp dụng phương pháp giải phù hợp.
- Rèn luyện tư duy logic: Phát triển khả năng tư duy logic giúp bạn suy luận logic, giải quyết vấn đề một cách nhanh chóng và chính xác.
Kết Luận
Bài viết đã cung cấp cho bạn những kiến thức cơ bản và phương pháp giải bất phương trình lớp 9 hiệu quả. Hy vọng rằng bài viết này sẽ giúp bạn tự tin hơn trong việc học tập và giải quyết các bài tập liên quan đến giải bất phương trình lớp 9.
FAQ
1. Sự khác nhau giữa phương trình và bất phương trình là gì?
Phương trình là một đẳng thức toán học, trong khi bất phương trình là một mệnh đề so sánh giữa hai vế, sử dụng các dấu >, <, ≥, ≤.
2. Khi nào cần đổi chiều bất đẳng thức?
Khi nhân hoặc chia cả hai vế của bất phương trình với cùng một số âm, ta cần đổi chiều bất đẳng thức.
3. Làm thế nào để kiểm tra xem một giá trị có phải là nghiệm của bất phương trình hay không?
Thay giá trị đó vào bất phương trình ban đầu. Nếu bất phương trình đúng, thì giá trị đó là nghiệm của bất phương trình.
Bạn cần hỗ trợ?
Liên hệ ngay với chúng tôi!
- Số Điện Thoại: 02033846993
- Email: [email protected]
- Địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam.
Đội ngũ Giải Bóng luôn sẵn sàng hỗ trợ bạn 24/7!
Hãy tiếp tục theo dõi giải phương trình và bất phương trình lớp 9 để cập nhật thêm nhiều kiến thức bổ ích!