Tích phân là một công cụ mạnh mẽ trong toán học, đặc biệt hữu ích khi được ứng dụng để giải quyết các bài toán trong hình học. Việc Giải Bài Tập ứng Dụng Tích Phân Trong Hình Học không chỉ giúp bạn hiểu sâu hơn về bản chất của tích phân mà còn rèn luyện tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Hiểu Rõ Bản Chất Vấn Đề
Trước khi đi vào giải quyết các bài toán cụ thể, điều quan trọng là phải hiểu rõ bản chất của việc ứng dụng tích phân trong hình học. Về cơ bản, tích phân cho phép chúng ta tính toán các đại lượng liên quan đến hình học như diện tích, thể tích, độ dài đường cong bằng cách chia nhỏ đối tượng hình học thành các phần tử vô cùng nhỏ, sau đó cộng diện tích hoặc thể tích của các phần tử này lại với nhau.
Các Bước Giải Bài Tập Ứng Dụng Tích Phân Trong Hình Học
Dưới đây là các bước chung để giải quyết các bài toán ứng dụng tích phân trong hình học:
- Xác định bài toán yêu cầu tính toán đại lượng gì: Diện tích hình phẳng, thể tích khối tròn xoay, hay độ dài đường cong?
- Vẽ hình: Minh họa hình học của bài toán sẽ giúp bạn hình dung rõ hơn về cách tiếp cận.
- Chọn hệ trục tọa độ phù hợp: Việc lựa chọn hệ trục tọa độ phù hợp sẽ đơn giản hóa việc tính toán.
- Chia nhỏ đối tượng hình học: Chia đối tượng thành các phần tử vô cùng nhỏ có dạng hình học đơn giản (hình chữ nhật, hình tròn, hình trụ…).
- Lập công thức tính diện tích/thể tích/độ dài của một phần tử: Sử dụng kiến thức hình học cơ bản để thiết lập công thức.
- Lập tích phân: Biểu diễn tổng diện tích/thể tích/độ dài của tất cả các phần tử bằng một tích phân xác định.
- Tính tích phân: Sử dụng các phương pháp tính tích phân đã học để tính toán kết quả cuối cùng.
Một Số Dạng Bài Tập Phổ Biến
Dưới đây là một số dạng bài tập ứng dụng tích phân trong hình học thường gặp:
1. Tính Diện Tích Hình Phẳng
Bài toán: Cho đường cong y = f(x), trục hoành và hai đường thẳng x = a, x = b (a < b). Tính diện tích hình phẳng giới hạn bởi các đường đã cho.
Cách giải:
- Vẽ đồ thị hàm số y = f(x).
- Chia hình phẳng thành các hình chữ nhật nhỏ có chiều rộng là dx và chiều cao là |f(x)|.
- Diện tích một hình chữ nhật nhỏ là dS = |f(x)|dx.
- Diện tích hình phẳng được tính bằng tích phân: S = ∫ab |f(x)| dx.
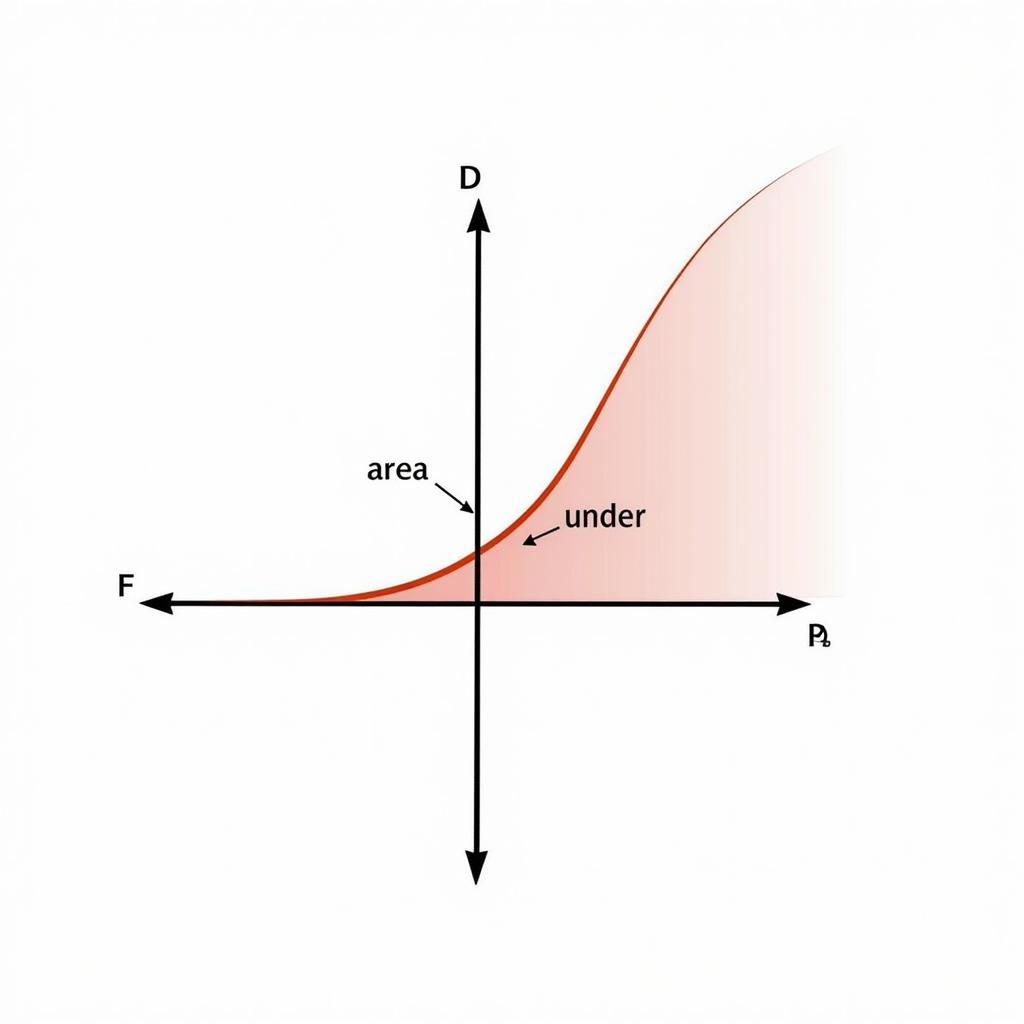Tính Diện Tích Hình Phẳng Bằng Tích Phân
2. Tính Thể Tích Khối Tròn Xoay
Bài toán: Cho đường cong y = f(x), trục hoành và hai đường thẳng x = a, x = b (a < b). Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường đã cho quanh trục hoành.
Cách giải:
- Vẽ đồ thị hàm số y = f(x).
- Chia hình phẳng thành các hình chữ nhật nhỏ có chiều rộng là dx và chiều cao là f(x).
- Khi quay hình chữ nhật nhỏ quanh trục hoành, ta được một đĩa tròn mỏng có bán kính đáy là f(x) và chiều cao là dx.
- Thể tích đĩa tròn mỏng là dV = π[f(x)]2dx.
- Thể tích khối tròn xoay được tính bằng tích phân: V = π∫ab [f(x)]2 dx.
3. Tính Độ Dài Đường Cong
Bài toán: Cho đường cong y = f(x) xác định trên đoạn [a, b]. Tính độ dài đường cong đó.
Cách giải:
- Chia đường cong thành các đoạn thẳng nhỏ có độ dài là ds.
- Theo định lý Pytago, ta có ds = √(dx2 + dy2) = √[1 + (dy/dx)2]dx.
- Độ dài đường cong được tính bằng tích phân: L = ∫ab √[1 + (f'(x))2] dx.
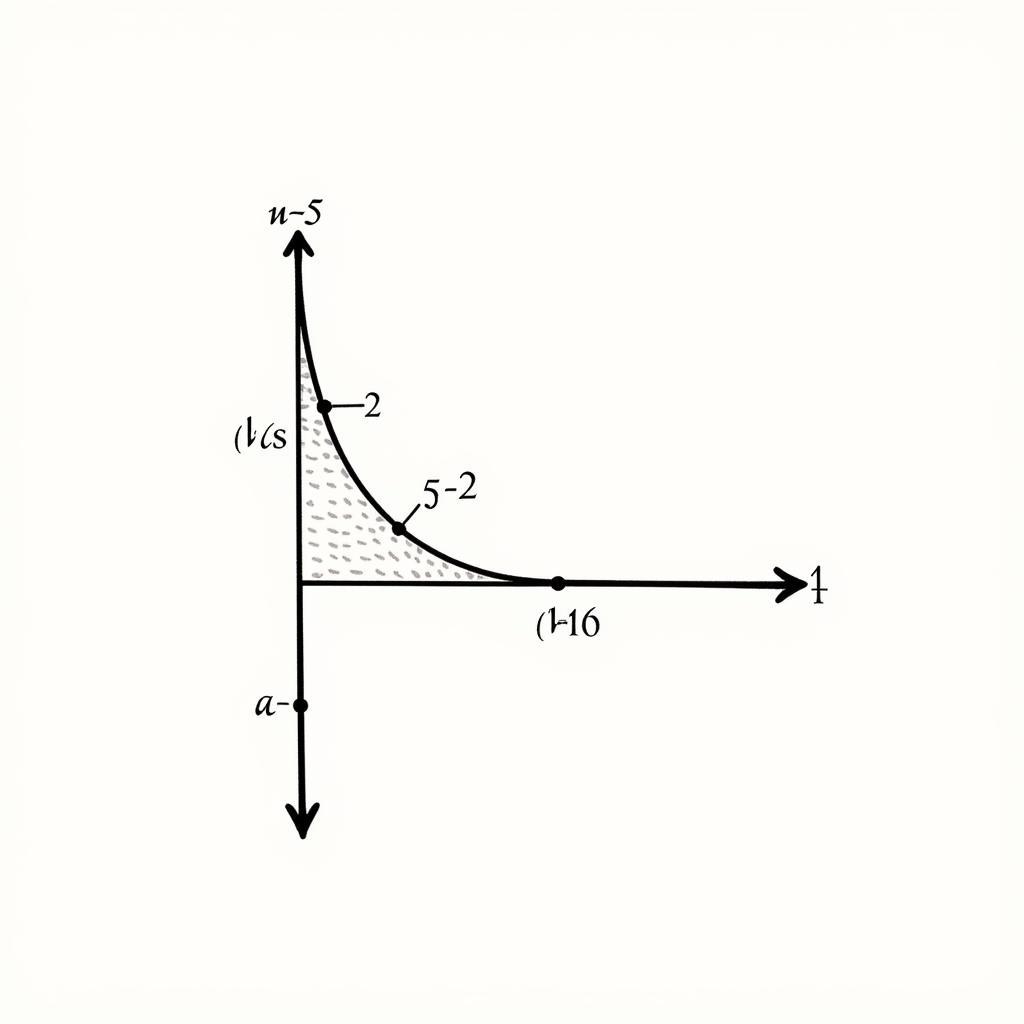Tính Độ Dài Đường Cong Bằng Tích Phân
Kết Luận
Việc giải bài tập ứng dụng tích phân trong hình học đòi hỏi sự kết hợp nhuần nhuyễn giữa kiến thức tích phân và hình học. Bằng cách nắm vững các bước giải bài toán, làm nhiều bài tập và tham khảo các tài liệu liên quan, bạn sẽ ngày càng tự tin hơn trong việc giải quyết các bài toán thuộc dạng này.
Bạn Cần Hỗ Trợ?
Nếu bạn gặp khó khăn trong việc giải bài tập ứng dụng tích phân trong hình học hoặc muốn tìm hiểu thêm về các chủ đề toán học khác, hãy liên hệ với chúng tôi:
- Số Điện Thoại: 02033846993
- Email: [email protected]
- Địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam
Chúng tôi có đội ngũ chăm sóc khách hàng 24/7 luôn sẵn sàng hỗ trợ bạn. Đừng ngần ngại liên hệ!