Giải Bài Tập Toán Cao Cấp 1 Chương 3 là một bước quan trọng để nắm vững kiến thức về các khái niệm cơ bản của giải tích hàm nhiều biến. Chương này thường tập trung vào các chủ đề như giới hạn, đạo hàm, vi phân, và ứng dụng của chúng. Việc hiểu rõ các khái niệm này sẽ tạo nền tảng vững chắc cho việc học các chương tiếp theo. Bạn có thể tham khảo thêm về giải pháp thiếu hụt nhân sự.
Đạo Hàm Riêng và Vi Phân Toàn Phần
Đạo hàm riêng của một hàm nhiều biến là đạo hàm theo một biến, coi các biến khác là hằng số. Vi phân toàn phần biểu diễn sự thay đổi của hàm số khi tất cả các biến độc lập cùng thay đổi một lượng nhỏ. Hiểu rõ hai khái niệm này là chìa khóa để giải quyết nhiều bài tập trong chương 3.
Việc tính đạo hàm riêng và vi phân toàn phần đòi hỏi sự cẩn thận và chính xác. Một lỗi nhỏ trong quá trình tính toán có thể dẫn đến kết quả sai. Chính vì vậy, luyện tập thường xuyên là rất quan trọng.
Đạo hàm riêng và vi phân toàn phần
Ứng Dụng của Đạo Hàm và Vi Phân
Đạo hàm và vi phân có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực khác. Trong chương 3, bạn sẽ học cách áp dụng chúng để tìm cực trị của hàm nhiều biến, giải bài toán tối ưu, và xấp xỉ giá trị hàm số. Việc nắm vững các ứng dụng này sẽ giúp bạn giải quyết các bài toán thực tế. Nếu cần tìm hiểu thêm về các bài tập Excel, bạn có thể xem tại bài tập excel tin học đại cương có lời giải.
Tìm Cực Trị của Hàm Nhiều Biến
Việc tìm cực trị của hàm nhiều biến là một ứng dụng quan trọng của đạo hàm riêng. Bằng cách giải hệ phương trình đạo hàm riêng bằng 0, ta có thể tìm được các điểm dừng. Sau đó, sử dụng ma trận Hessian, ta có thể xác định được điểm dừng đó là cực đại, cực tiểu hay điểm yên ngựa.
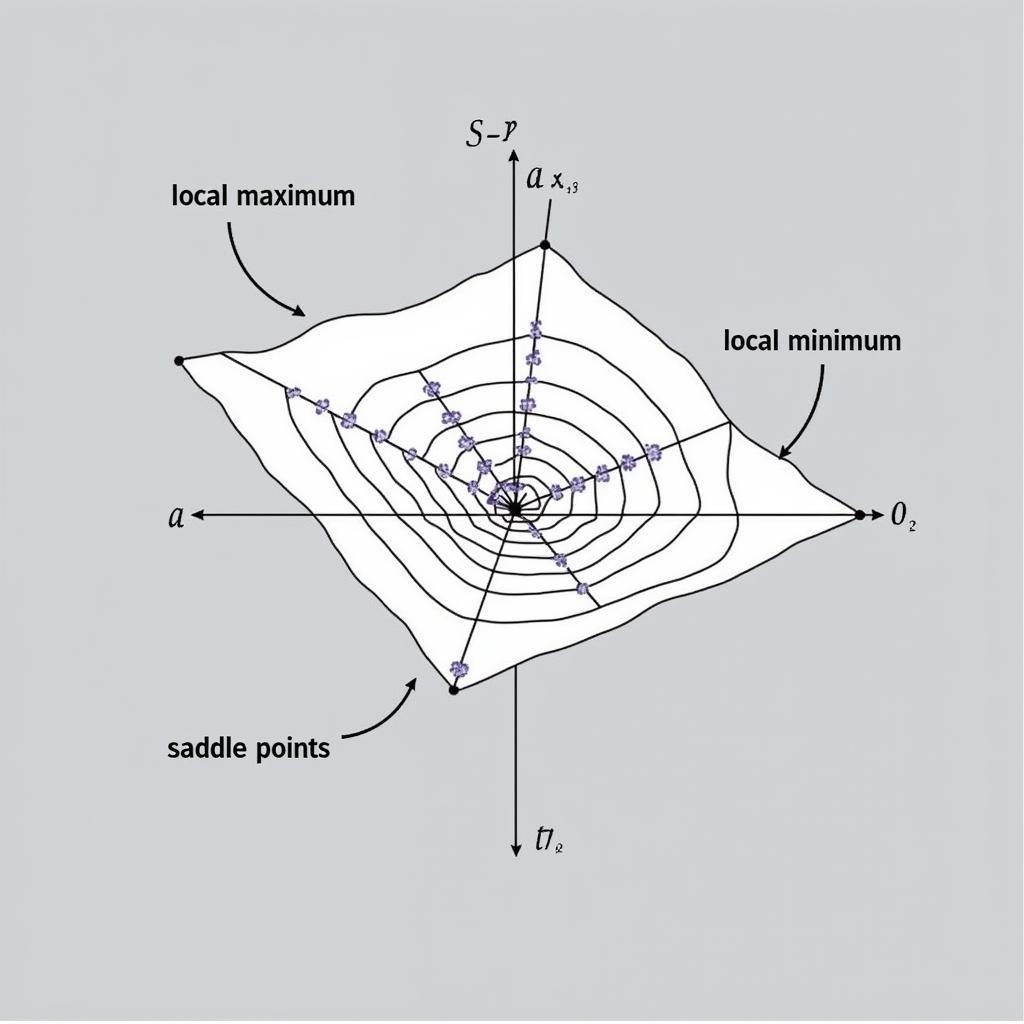Tìm cực trị hàm nhiều biến
Giải Bài Tập Toán Cao Cấp 1 Chương 3: Phương Pháp Học Tập Hiệu Quả
Để giải quyết hiệu quả các bài tập toán cao cấp 1 chương 3, bạn cần nắm vững lý thuyết và luyện tập thường xuyên. Hãy bắt đầu bằng việc đọc kỹ giáo trình và ghi chép lại các công thức quan trọng. Sau đó, hãy làm các bài tập ví dụ và bài tập trong sách giáo khoa. Nếu gặp khó khăn, hãy tham khảo lời giải hoặc hỏi thầy cô, bạn bè. Bạn cũng có thể tìm hiểu về giải sgk vật lí 10 để có thêm kiến thức về vật lý.
Theo GS.TS Nguyễn Văn A, chuyên gia Toán học: “Việc luyện tập thường xuyên là chìa khóa để thành công trong môn Toán Cao Cấp. Hãy dành thời gian mỗi ngày để làm bài tập và ôn lại kiến thức.”
Kết luận
Giải bài tập toán cao cấp 1 chương 3 là một quá trình đòi hỏi sự kiên trì và nỗ lực. Bằng cách nắm vững lý thuyết, luyện tập thường xuyên và áp dụng các phương pháp học tập hiệu quả, bạn sẽ có thể vượt qua mọi khó khăn và đạt được kết quả tốt. Hãy nhớ rằng việc hiểu rõ các khái niệm trong chương 3 là nền tảng quan trọng cho việc học các chương tiếp theo của toán cao cấp. thi giải toán qua mạng lớp 3 cũng là một lựa chọn thú vị để rèn luyện kỹ năng toán học.
Phương pháp học tập hiệu quả Toán Cao Cấp
FAQ
- Đạo hàm riêng là gì?
- Vi phân toàn phần là gì?
- Làm thế nào để tìm cực trị của hàm nhiều biến?
- Ứng dụng của đạo hàm và vi phân trong chương 3 là gì?
- Làm thế nào để học hiệu quả toán cao cấp 1 chương 3?
- Ma trận Hessian là gì và được sử dụng như thế nào?
- Làm thế nào để tính đạo hàm riêng của hàm ẩn?
Mô tả các tình huống thường gặp câu hỏi.
Sinh viên thường gặp khó khăn trong việc áp dụng công thức tính đạo hàm riêng và vi phân toàn phần, đặc biệt là với các hàm phức tạp. Việc xác định cực trị của hàm nhiều biến cũng là một thách thức, đòi hỏi sự hiểu biết sâu sắc về ma trận Hessian.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các chủ đề liên quan như tích phân bội, tích phân đường, tích phân mặt trên website.