Giải Bài Tập Toán 9 Bài 29 Trang 59 là cách hiệu quả để học sinh lớp 9 ôn tập và củng cố kiến thức về hệ thức lượng trong tam giác vuông. Bài viết này sẽ cung cấp cho bạn hướng dẫn chi tiết về cách giải các bài tập trong sách giáo khoa toán 9 trang 59, kèm theo những lời khuyên hữu ích để bạn có thể tự tin chinh phục các dạng bài tập liên quan đến hệ thức lượng.
Hướng dẫn giải bài tập toán 9 bài 29 trang 59
Bài tập 84
Đề bài:
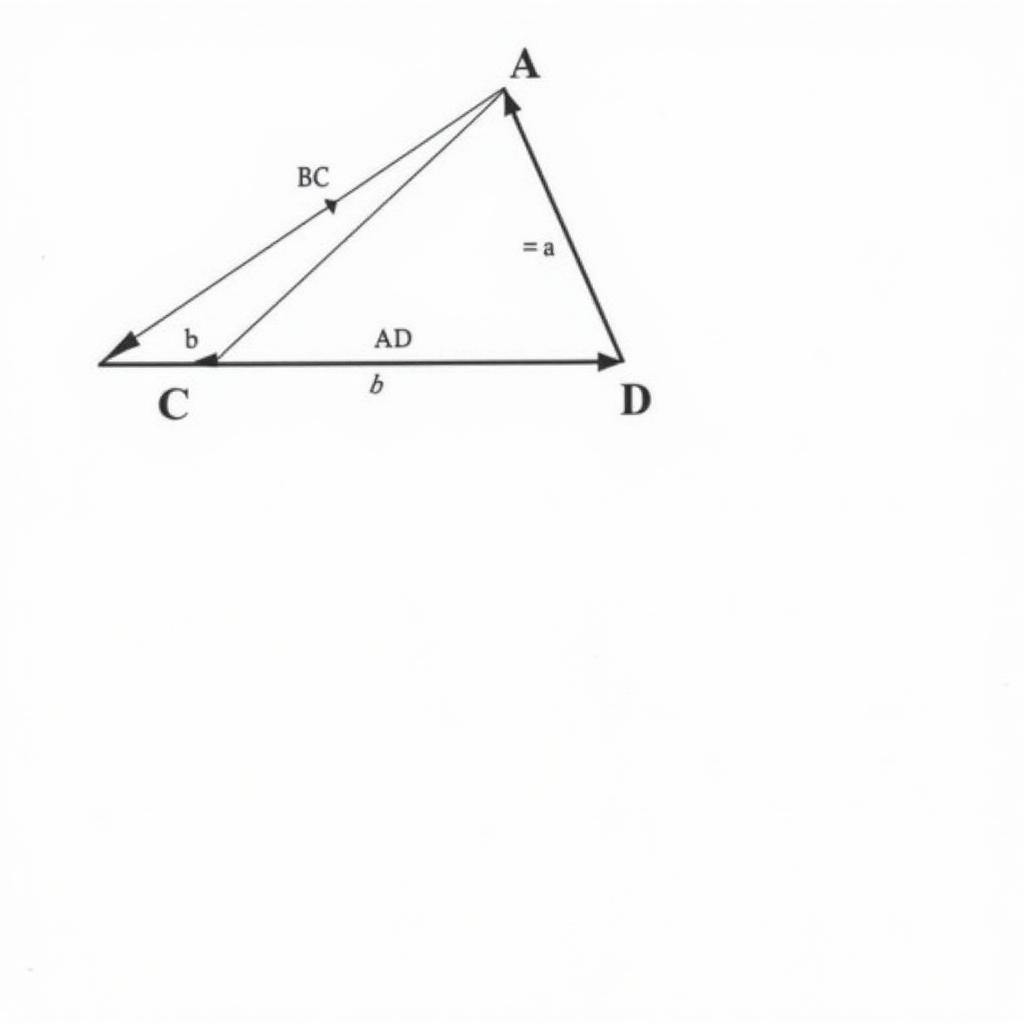hình vẽ bài tập 84
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = c, AC = b, BC = a, AH = h, BH = c’, CH = b’.
Yêu cầu:
Chứng minh các công thức sau:
a) $ab = h.c$
b) $h^2 = b’.c’$
c) $frac{1}{h^2} = frac{1}{b^2} + frac{1}{c^2}$
Lời giải:
a) Xét tam giác ABC vuông tại A, ta có:
- Diện tích tam giác ABC: $S_{ABC} = frac{1}{2}AB.AC = frac{1}{2}bc$
- Diện tích tam giác ABC (tính theo đường cao AH): $S_{ABC} = frac{1}{2}AH.BC = frac{1}{2}hc$
Từ đó suy ra: $frac{1}{2}bc = frac{1}{2}hc$
$Rightarrow ab = hc$ (đpcm)
chứng minh công thức hệ thức lượng
b) Xét tam giác AHB và tam giác CHA, ta có:
- $widehat{AHB} = widehat{CHA} = 90^circ$
- $widehat{BAH} = widehat{ACH}$ (cùng phụ với góc B)
Do đó, tam giác AHB đồng dạng với tam giác CHA (g.g)
$Rightarrow frac{AH}{CH} = frac{BH}{AH}$
$Rightarrow AH^2 = BH.CH$
$Rightarrow h^2 = b’.c’$ (đpcm)
c) Từ công thức $ab = hc$, ta có: $h = frac{ab}{c}$
Thay vào công thức $h^2 = b’.c’$, ta được:
$(frac{ab}{c})^2 = b’.c’$
$Rightarrow frac{a^2b^2}{c^2} = b’.c’$
$Rightarrow a^2 = frac{b’.c’.c^2}{b^2}$
$Rightarrow frac{1}{a^2} = frac{b^2}{b’.c’.c^2}$
Mà $a^2 = b^2 + c^2$ (định lý Pytago)
Nên: $frac{1}{b^2 + c^2} = frac{b^2}{b’.c’.c^2}$
$Rightarrow frac{1}{b^2} + frac{1}{c^2} = frac{1}{h^2}$ (đpcm)
Bài tập 85
Đề bài:
Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 12cm, BC = 13cm. Tính AB, AH, BH, CH.
Lời giải:
Áp dụng định lý Pytago trong tam giác ABC vuông tại A, ta có:
$AB = sqrt{BC^2 – AC^2} = sqrt{13^2 – 12^2} = 5cm$
Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:
- $AB.AC = AH.BC Rightarrow AH = frac{AB.AC}{BC} = frac{5.12}{13} = frac{60}{13}cm$
- $AB^2 = BH.BC Rightarrow BH = frac{AB^2}{BC} = frac{5^2}{13} = frac{25}{13}cm$
- $CH = BC – BH = 13 – frac{25}{13} = frac{144}{13}cm$
Một số lưu ý khi giải bài tập toán 9 bài 29 trang 59
- Nắm vững các hệ thức lượng trong tam giác vuông.
- Vẽ hình chính xác và đầy đủ để dễ dàng áp dụng các hệ thức lượng.
- Chú ý đến đơn vị của các đại lượng trong bài toán.
- Luyện tập giải nhiều dạng bài tập khác nhau để nâng cao kỹ năng giải toán.
Kết luận
Bài viết đã hướng dẫn chi tiết cách giải các bài tập trong sách giáo khoa toán 9 bài 29 trang 59. Hy vọng rằng, qua bài viết này, các em học sinh sẽ nắm vững hơn kiến thức về hệ thức lượng trong tam giác vuông và tự tin giải quyết các bài tập liên quan.
FAQ
1. Hệ thức lượng trong tam giác vuông là gì?
Hệ thức lượng trong tam giác vuông là tập hợp các công thức liên hệ giữa các cạnh và các đường trong tam giác vuông, giúp ta tính toán các đại lượng chưa biết trong tam giác vuông.
2. Có những hệ thức lượng nào trong tam giác vuông?
Một số hệ thức lượng cơ bản trong tam giác vuông:
- $b^2 = a.b’$
- $c^2 = a.c’$
- $h^2 = b’.c’$
- $ab = h.c$
- $frac{1}{h^2} = frac{1}{b^2} + frac{1}{c^2}$
3. Làm thế nào để nhớ được các hệ thức lượng trong tam giác vuông?
Có thể học thuộc lòng các hệ thức lượng, tuy nhiên, cách hiệu quả hơn là hiểu rõ cách chứng minh các công thức này. Khi đã hiểu rõ bản chất, bạn sẽ dễ dàng ghi nhớ và áp dụng chúng vào giải bài tập.
Các câu hỏi khác
- Bài 28 trang 58
- Bài 30 trang 59
Bạn cần hỗ trợ?
Liên hệ ngay với chúng tôi:
- Số điện thoại: 02033846993
- Email: [email protected]
- Địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam
Đội ngũ chăm sóc khách hàng của chúng tôi luôn sẵn sàng hỗ trợ bạn 24/7!