Hình học 11 chương 1 đặt nền móng cho cả chương trình hình học không gian lớp 11, trang bị cho bạn những kiến thức quan trọng về đường thẳng, mặt phẳng trong không gian và mối quan hệ giữa chúng. Nắm vững nội dung chương này sẽ giúp bạn tự tin hơn khi giải các bài tập hình học phức tạp ở các chương sau.
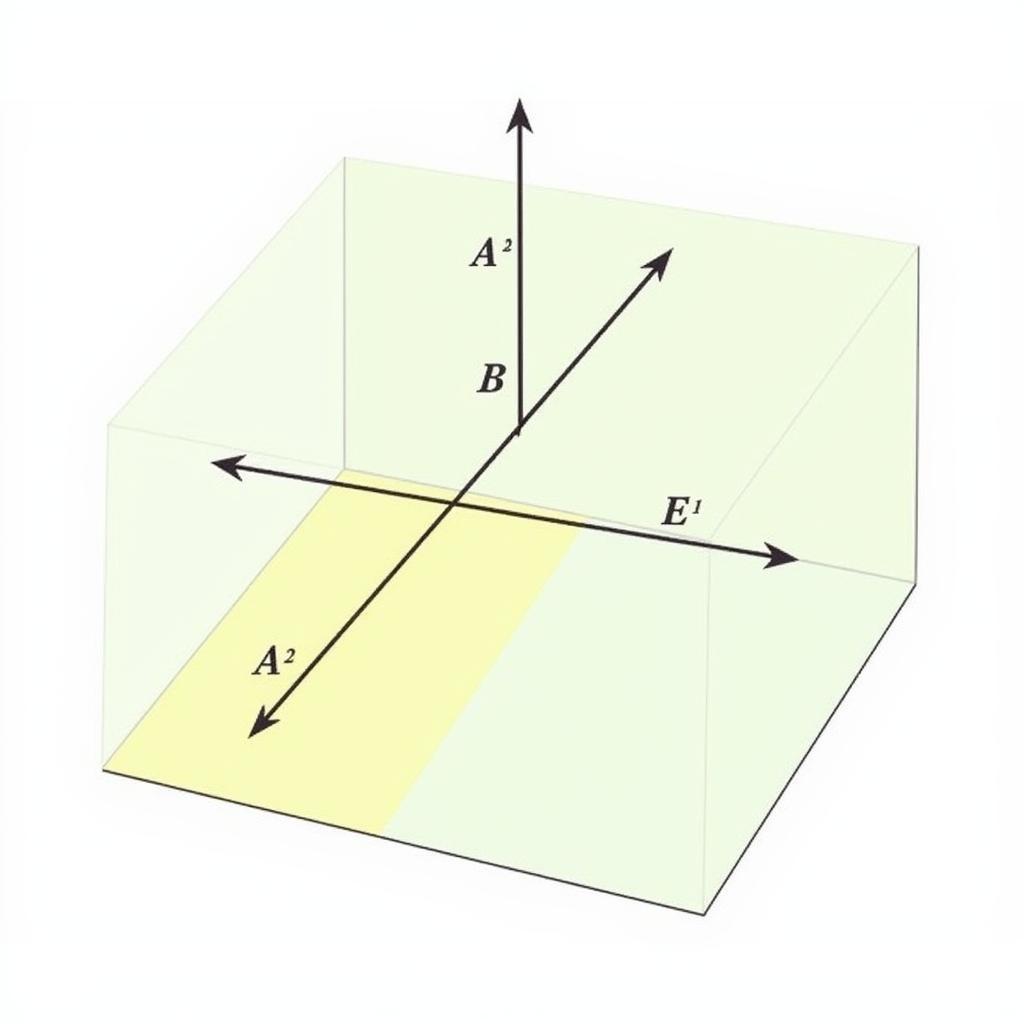 Quan hệ song song giữa hai đường thẳng
Quan hệ song song giữa hai đường thẳng
Khái Niệm Cơ Bản Về Hình Học Không Gian
Trong hình học không gian, ta không còn giới hạn trong mặt phẳng như hình học phẳng mà thay vào đó là một không gian ba chiều.
Điểm, Đường Thẳng, Mặt Phẳng
- Điểm: Được coi là yếu tố cơ bản nhất, không có kích thước và được kí hiệu bằng chữ cái in hoa (A, B, C…).
- Đường thẳng: Là tập hợp vô số điểm thẳng hàng với nhau, không có bề rộng và kéo dài vô hạn về hai phía. Đường thẳng được kí hiệu bằng chữ cái thường (a, b, c…).
- Mặt phẳng: Là tập hợp vô số điểm, đường thẳng cùng nằm trên một bề mặt phẳng, không có độ dày và kéo dài vô hạn về mọi phía. Mặt phẳng thường được kí hiệu bằng chữ cái Hy Lạp (α, β, γ…).
 Vị trí tương đối của điểm, đường thẳng, mặt phẳng
Vị trí tương đối của điểm, đường thẳng, mặt phẳng
Quan Hệ Giữa Các Yếu Tố
- Hai đường thẳng: Có thể song song, cắt nhau hoặc chéo nhau.
- Đường thẳng và mặt phẳng: Có thể song song, cắt nhau hoặc đường thẳng nằm trong mặt phẳng.
- Hai mặt phẳng: Có thể song song hoặc cắt nhau.
Các Tính Chất Quan Trọng
Tính Chất Hai Đường Thẳng Song Song
- Hai đường thẳng song song được chứa trong một mặt phẳng.
- Qua một điểm nằm ngoài một đường thẳng, có duy nhất một đường thẳng song song với đường thẳng đó.
Tính Chất Hai Mặt Phẳng Song Song
- Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến (nếu có) của chúng cũng song song với hai đường thẳng đó.
- Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì nó cũng cắt mặt phẳng còn lại.
Định Lý Thales Trong Không Gian
Ba mặt phẳng song song chắn trên hai đường thẳng bất kì các đoạn thẳng tương ứng tỉ lệ.
Phương Pháp Giải Bài Tập Hình Học 11 Chương 1
- Nắm vững kiến thức lý thuyết: Đây là bước đầu tiên và quan trọng nhất để giải quyết bất kỳ bài toán nào. Hãy chắc chắn bạn hiểu rõ các định nghĩa, định lý và tính chất đã được học.
- Phân tích đề bài: Xác định rõ yêu cầu của đề bài, xác định các yếu tố đã biết và yếu tố cần tìm.
- Vẽ hình: Hình vẽ minh họa là một công cụ đắc lực giúp bạn hình dung không gian và các mối quan hệ giữa các yếu tố trong bài toán.
- Sử dụng các tính chất, định lý: Áp dụng linh hoạt các kiến thức đã học để giải quyết bài toán.
- Kiểm tra lại kết quả: Sau khi tìm ra đáp án, hãy kiểm tra lại xem kết quả có hợp lý và chính xác hay không.
Một Số Dạng Bài Tập Thường Gặp
Dạng 1: Xác Định Vị Trí Tương Đối
Bài toán yêu cầu xác định vị trí tương đối giữa các yếu tố như hai đường thẳng, đường thẳng và mặt phẳng, hai mặt phẳng.
Ví dụ: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Xác định vị trí tương đối của:
- Đường thẳng SA và đường thẳng CD
- Đường thẳng SB và mặt phẳng (SAD)
- Mặt phẳng (SAB) và mặt phẳng (SCD)
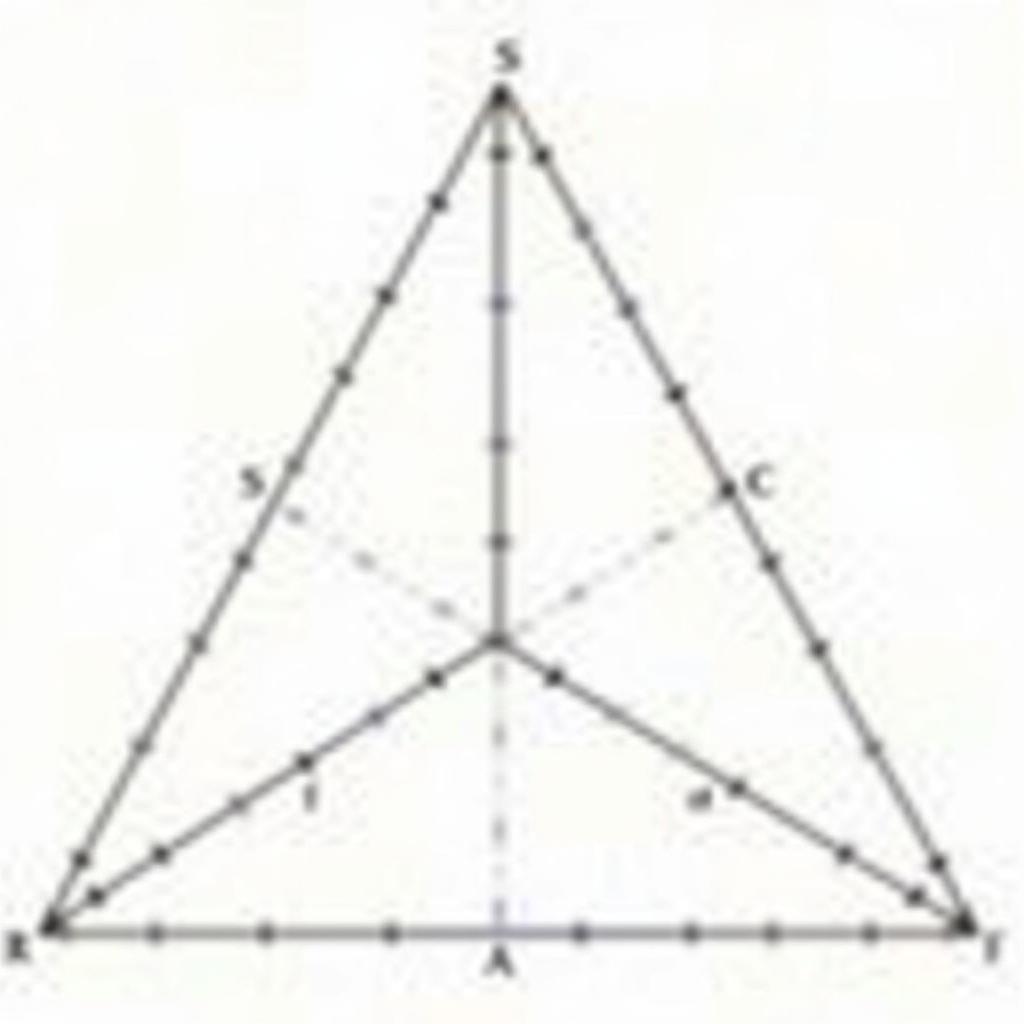 Xác định vị trí tương đối của các yếu tố trong không gian
Xác định vị trí tương đối của các yếu tố trong không gian
Dạng 2: Chứng Minh Song Song
Bài toán yêu cầu chứng minh hai đường thẳng song song, đường thẳng song song với mặt phẳng, hoặc hai mặt phẳng song song.
Ví dụ: Cho hình chóp S.ABCD, đáy ABCD là hình thang, AB // CD. M là trung điểm của SD. Chứng minh:
- AM // (SBC)
- (SAD) // (SBC)
Dạng 3: Tìm Giao Tuyến Của Hai Mặt Phẳng
Bài toán yêu cầu tìm giao tuyến của hai mặt phẳng, thường sử dụng phương pháp tìm hai điểm chung của hai mặt phẳng đó.
Ví dụ: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
Kết Luận
Hy vọng bài viết đã cung cấp cho bạn những kiến thức hữu ích và phương pháp hiệu quả để Giải Bài Tập Hình Học 11 Chương 1. Nắm vững chương này sẽ là nền tảng vững chắc để bạn tiếp tục chinh phục những kiến thức phức tạp hơn trong hình học không gian.
FAQ
1. Làm thế nào để phân biệt được hai đường thẳng chéo nhau và hai đường thẳng cắt nhau?
Hai đường thẳng chéo nhau không nằm trong cùng một mặt phẳng, trong khi hai đường thẳng cắt nhau thì cùng nằm trong một mặt phẳng và có một điểm chung.
2. Khi nào một đường thẳng song song với một mặt phẳng?
Một đường thẳng song song với một mặt phẳng khi chúng không có điểm chung nào.
3. Làm thế nào để chứng minh hai mặt phẳng song song?
Có thể chứng minh hai mặt phẳng song song bằng cách chứng minh chúng cùng song song với một đường thẳng hoặc sử dụng tính chất hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song.
Bạn Cần Thêm Trợ Giúp?
Hãy xem các bài viết khác trên trang web của chúng tôi để tìm hiểu thêm về giải hóa sgk 10, bài tập tự luận vật lý 11 có lời giải và giải toán 10.
Bạn cũng có thể tìm thấy thông tin hữu ích về 12 rủi ro trong tmđt và cách giải quyết và giải bài tập sinh học bài 47.
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
