Cách Giải Hệ Phương Trình Bậc Nhất

Puskasvào
Giải hệ phương trình bậc nhất bằng phương pháp cộng đại số

Hệ phương trình bậc nhất là một khái niệm toán học cơ bản, xuất hiện từ bậc trung học cơ sở và được sử dụng rộng rãi trong nhiều lĩnh vực. Cách Giải Hệ Phương Trình Bậc Nhất là một trong những kỹ năng quan trọng mà học sinh cần nắm vững. Bài viết này sẽ hướng dẫn chi tiết cách giải hệ phương trình bậc nhất, từ cơ bản đến nâng cao.

Xem thêm phương trình bậc nhất một ẩn và cách giải.

Hệ Phương Trình Bậc Nhất Hai Ẩn

Hệ phương trình bậc nhất hai ẩn có dạng:

a1x + b1y = c1
a2x + b2y = c2

Trong đó, x và y là ẩn, a1, b1, c1, a2, b2, c2 là các hệ số. Có nhiều phương pháp để giải hệ phương trình bậc nhất hai ẩn, bao gồm phương pháp thế, phương pháp cộng đại số và phương pháp đồ thị.

Phương Pháp Thế

Phương pháp thế bao gồm việc biểu diễn một ẩn theo ẩn còn lại từ một phương trình, sau đó thay vào phương trình còn lại để tìm ra giá trị của ẩn đó.

  1. Bước 1: Chọn một phương trình và biểu diễn một ẩn theo ẩn còn lại.
  2. Bước 2: Thay biểu thức tìm được ở bước 1 vào phương trình còn lại.
  3. Bước 3: Giải phương trình một ẩn vừa tìm được.
  4. Bước 4: Thay giá trị của ẩn vừa tìm được vào biểu thức ở bước 1 để tìm giá trị của ẩn còn lại.

Phương Pháp Cộng Đại Số

Phương pháp cộng đại số dựa trên việc nhân hai vế của mỗi phương trình với một số sao cho hệ số của một ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau. Sau đó, cộng hoặc trừ hai phương trình để khử đi một ẩn và tìm ra giá trị của ẩn còn lại.

  1. Bước 1: Chọn một ẩn để khử.
  2. Bước 2: Nhân hai vế của mỗi phương trình với một số sao cho hệ số của ẩn được chọn ở hai phương trình bằng nhau hoặc đối nhau.
  3. Bước 3: Cộng hoặc trừ hai phương trình để khử ẩn đã chọn.
  4. Bước 4: Giải phương trình một ẩn vừa tìm được.
  5. Bước 5: Thay giá trị của ẩn vừa tìm được vào một trong hai phương trình ban đầu để tìm giá trị của ẩn còn lại.

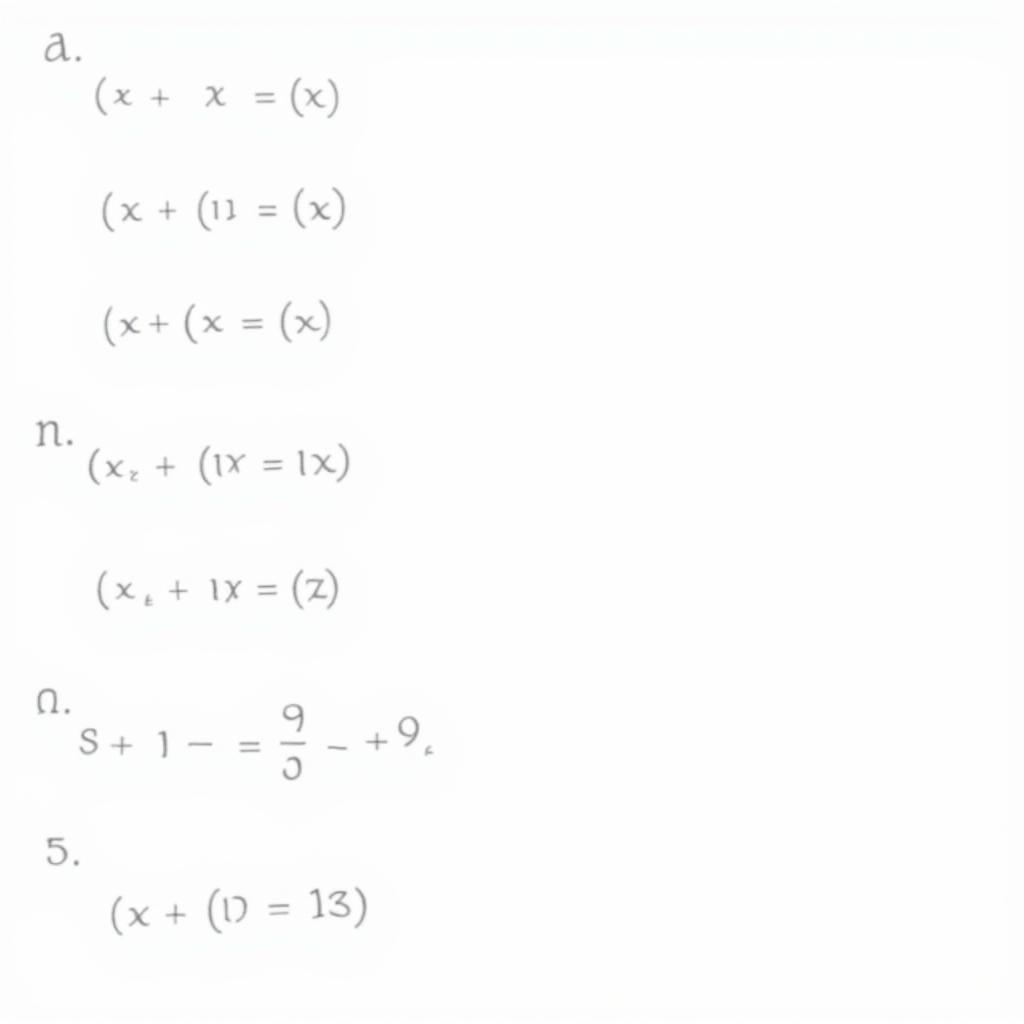Giải hệ phương trình bậc nhất bằng phương pháp cộng đại sốGiải hệ phương trình bậc nhất bằng phương pháp cộng đại số

“Phương pháp cộng đại số đòi hỏi sự tính toán cẩn thận để tránh sai sót trong quá trình nhân và cộng trừ,” – Nguyễn Văn An, Giảng viên Toán học tại Đại học Sư Phạm Hà Nội.

Phương Pháp Đồ Thị

Phương pháp đồ thị dựa trên việc vẽ đồ thị của hai phương trình trên cùng một hệ trục tọa độ. Giao điểm của hai đồ thị chính là nghiệm của hệ phương trình.

  1. Bước 1: Vẽ đồ thị của hai phương trình trên cùng một hệ trục tọa độ.
  2. Bước 2: Xác định tọa độ giao điểm của hai đồ thị. Tọa độ giao điểm chính là nghiệm của hệ phương trình.

Tham khảo thêm bài tập giải hệ phương tri2nh bậc nhất 2 ẩn.

Hệ Phương Trình Bậc Nhất Ba Ẩn

Hệ phương trình bậc nhất ba ẩn có dạng:

a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3

Các phương pháp giải hệ phương trình bậc nhất ba ẩn cũng tương tự như hệ phương trình bậc nhất hai ẩn, bao gồm phương pháp thế, phương pháp cộng đại số.

“Việc giải hệ phương trình bậc nhất ba ẩn đòi hỏi sự kiên nhẫn và kỹ năng tính toán tốt,” – Trần Thị Bình, Giáo viên Toán THPT Chuyên Hà Nội – Amsterdam.

Bạn cũng có thể tìm hiểu thêm về bài tập luyện tập giải phương trình.

Kết luận

Cách giải hệ phương trình bậc nhất là một kỹ năng quan trọng trong toán học. Bài viết đã trình bày các phương pháp cơ bản để giải hệ phương trình bậc nhất hai ẩn và ba ẩn. Nắm vững các phương pháp này sẽ giúp bạn giải quyết nhiều bài toán trong học tập và cuộc sống.

“Ứng dụng của hệ phương trình bậc nhất rất đa dạng, từ việc tính toán đơn giản đến các vấn đề phức tạp trong khoa học và kỹ thuật,” – Lê Văn Cường, Tiến sĩ Toán học.

FAQ

  1. Khi nào hệ phương trình bậc nhất vô nghiệm?
  2. Khi nào hệ phương trình bậc nhất có vô số nghiệm?
  3. Phương pháp nào giải hệ phương trình bậc nhất nhanh nhất?
  4. Làm thế nào để kiểm tra nghiệm của hệ phương trình bậc nhất?
  5. Ứng dụng của hệ phương trình bậc nhất trong thực tế là gì?
  6. Có phần mềm nào hỗ trợ giải hệ phương trình bậc nhất không?
  7. Hệ phương trình bậc nhất có bao nhiêu nghiệm?

Bạn có thể tham khảo thêm giải toán 9 trang 111 và giải toán 10 đại số trang 154.

Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.