Bài toán thể tích lớp 9 là một trong những dạng toán quan trọng, thường xuất hiện trong các bài kiểm tra và kỳ thi chuyển cấp. Nắm vững kiến thức và phương pháp giải bài tập thể tích lớp 9 có lời giải Violet sẽ giúp các em học sinh tự tin chinh phục dạng toán này.
Các Dạng Bài Toán Thể Tích Lớp 9 Thường Gặp
Dưới đây là một số dạng bài toán thể tích lớp 9 thường gặp:
- Dạng 1: Tính thể tích hình chóp đều:
- Bài toán yêu cầu tính thể tích hình chóp đều khi biết các dữ kiện như độ dài cạnh đáy, chiều cao, diện tích đáy, v.v.
- Dạng 2: Tính thể tích hình chóp cụt:
- Bài toán liên quan đến việc tính thể tích của hình chóp cụt khi biết các thông tin về hai đáy, chiều cao, v.v.
- Dạng 3: Tính thể tích hình lăng trụ đứng:
- Bài toán tập trung vào việc xác định thể tích hình lăng trụ đứng dựa trên các dữ kiện như diện tích đáy, chiều cao, v.v.
- Dạng 4: Tính thể tích hình nón:
- Yêu cầu học sinh tính thể tích hình nón khi biết bán kính đáy, đường sinh, chiều cao, v.v.
- Dạng 5: Tính thể tích hình nón cụt:
- Bài toán liên quan đến việc tính thể tích hình nón cụt, thường dựa trên thông tin về hai bán kính đáy, đường sinh, chiều cao, v.v.
- Dạng 6: Tính thể tích hình cầu:
- Học sinh cần tính thể tích hình cầu khi biết bán kính, đường kính, diện tích mặt cầu, v.v.
Phương Pháp Giải Bài Toán Thể Tích Lớp 9 Có Lời Giải Violet
Để giải quyết hiệu quả các dạng Bài Toán Thể Tích Lớp 9 Có Lời Giải Violet, học sinh cần nắm vững các công thức tính thể tích và áp dụng linh hoạt các phương pháp giải toán hình học không gian.
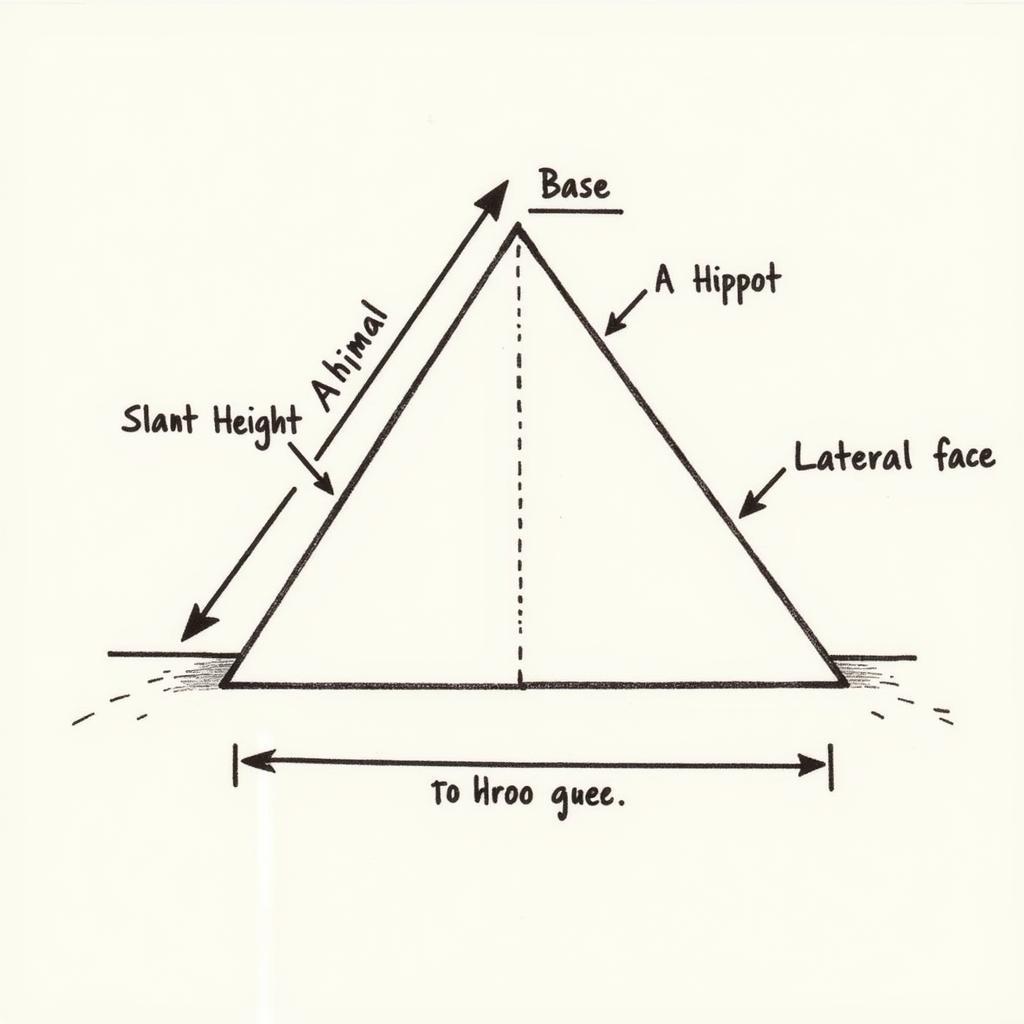Hình Chóp Đều
Công Thức Tính Thể Tích Các Hình Khối
Học thuộc các công thức tính thể tích là bước đầu tiên để giải quyết các bài toán liên quan. Dưới đây là tổng hợp công thức tính thể tích của các hình khối phổ biến trong chương trình lớp 9:
- Hình chóp đều: V = (1/3) Sđ h
- Trong đó:
- V là thể tích hình chóp đều
- Sđ là diện tích đáy hình chóp đều
- h là chiều cao hình chóp đều
- Trong đó:
- Hình chóp cụt: V = (1/3) h (S1 + S2 + √(S1 * S2))
- Trong đó:
- V là thể tích hình chóp cụt
- h là chiều cao hình chóp cụt
- S1 là diện tích đáy nhỏ
- S2 là diện tích đáy lớn
- Trong đó:
- Hình lăng trụ đứng: V = Sđ * h
- Trong đó:
- V là thể tích hình lăng trụ đứng
- Sđ là diện tích đáy
- h là chiều cao
- Trong đó:
- Hình nón: V = (1/3) π r^2 * h
- Trong đó:
- V là thể tích hình nón
- r là bán kính đáy
- h là chiều cao
- Trong đó:
- Hình nón cụt: V = (1/3) π h (R^2 + r^2 + R r)
- Trong đó:
- V là thể tích hình nón cụt
- h là chiều cao
- R là bán kính đáy lớn
- r là bán kính đáy nhỏ
- Trong đó:
- Hình cầu: V = (4/3) π R^3
- Trong đó:
- V là thể tích hình cầu
- R là bán kính hình cầu
- Trong đó:
Hình Nón Cụt
Các Phương Pháp Giải Toán Hình Học Không Gian
Bên cạnh việc ghi nhớ công thức, việc thành thạo các phương pháp giải toán hình học không gian cũng đóng vai trò quan trọng:
- Phương pháp trực tiếp: Áp dụng trực tiếp công thức, định lý, tính chất đã học để giải quyết bài toán.
- Phương pháp tọa độ trong không gian: Chuyển đổi bài toán hình học thành bài toán đại số bằng cách thiết lập hệ trục tọa độ Oxyz.
- Phương pháp dựng hình phụ: Bổ sung thêm hình vẽ để làm rõ mối quan hệ giữa các yếu tố trong bài toán.
- Phương pháp phản chứng: Giả sử điều cần chứng minh là sai, sau đó chứng minh điều giả sử đó dẫn đến mâu thuẫn.
Bài Tập Thể Tích Lớp 9 Có Lời Giải Violet
Bài tập 1: Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy bằng 60 độ. Tính thể tích khối chóp S.ABCD.
Lời giải:
- Gọi O là tâm của hình vuông ABCD.
- Ta có: SO ⊥ (ABCD) (Vì S.ABCD là hình chóp đều)
- Suy ra: góc giữa mặt bên (SCD) và mặt đáy (ABCD) là góc SOD = 60 độ.
- Xét tam giác vuông SOD, ta có:
- SO = OD tan(SOD) = (a√2)/2 tan(60 độ) = (a√6)/2
- Diện tích đáy ABCD: S(ABCD) = a^2
- Thể tích khối chóp S.ABCD:
- V(S.ABCD) = (1/3) S(ABCD) SO = (1/3) a^2 (a√6)/2 = (a^3√6)/6
Bài tập 2: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AB = a, AC = a√3, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’.
Lời giải:
- Diện tích đáy ABC: S(ABC) = (1/2) AB AC = (1/2) a a√3 = (a^2√3)/2
- Thể tích khối lăng trụ ABC.A’B’C’:
- V(ABC.A’B’C’) = S(ABC) AA’ = (a^2√3)/2 2a = a^3√3
Hình Lăng Trụ Đứng
Kết Luận
Bài viết đã cung cấp những kiến thức cơ bản và phương pháp giải bài toán thể tích lớp 9 có lời giải Violet. Hy vọng bài viết này sẽ giúp các em học sinh nắm vững kiến thức và tự tin hơn trong việc giải quyết các dạng bài tập liên quan đến thể tích hình học không gian.
FAQ
1. Làm cách nào để học tốt phần thể tích hình học không gian?
Học tốt phần thể tích hình học không gian đòi hỏi sự kết hợp của nhiều yếu tố: Nắm vững công thức tính thể tích của các hình khối, thành thạo các phương pháp giải toán hình học không gian, rèn luyện kỹ năng vẽ hình và tư duy logic.
2. Làm thế nào để phân biệt được các loại hình khối trong không gian?
Việc phân biệt các loại hình khối trong không gian dựa trên đặc điểm về mặt đáy, mặt bên, cạnh, đỉnh, góc. Ví dụ: Hình chóp có đáy là đa giác, mặt bên là tam giác; hình lăng trụ có hai đáy là hai đa giác bằng nhau và song song.
3. Ngoài Violet, còn có nguồn tài liệu nào uy tín để ôn tập phần thể tích hình học không gian?
Ngoài Violet, học sinh có thể tham khảo thêm các nguồn tài liệu uy tín như: Sách giáo khoa toán lớp 9, sách bài tập toán lớp 9, các website giáo dục uy tín, các video bài giảng trên Youtube,…
Bạn cần hỗ trợ?
Liên hệ ngay với chúng tôi:
Số Điện Thoại: 02033846993
Email: [email protected]
Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam.
Chúng tôi luôn sẵn sàng hỗ trợ bạn 24/7!