Bài Toán Mạch RL Giải Bằng Vi Phân: Nắm Vững Lý Thuyết và Luyện Tập Hiệu Quả

Puskasvào
Mạch điện RL

Bài toán mạch RL là một trong những bài toán cơ bản và quan trọng trong môn học Điện tử. Mạch RL bao gồm điện trở R và cuộn cảm L mắc nối tiếp, được sử dụng rộng rãi trong các mạch điện tử như bộ lọc, mạch điều khiển, và mạch dao động. Để giải quyết bài toán mạch RL, chúng ta thường sử dụng phương pháp vi phân, dựa trên các định luật cơ bản của điện từ học.

Cấu trúc Mạch RL và Phương Trình Vi Phân

Mạch RL đơn giản nhất bao gồm một điện trở R, một cuộn cảm L và một nguồn điện áp E (hoặc dòng điện I) được kết nối theo thứ tự đó. Dòng điện chạy qua mạch được kí hiệu là i(t).

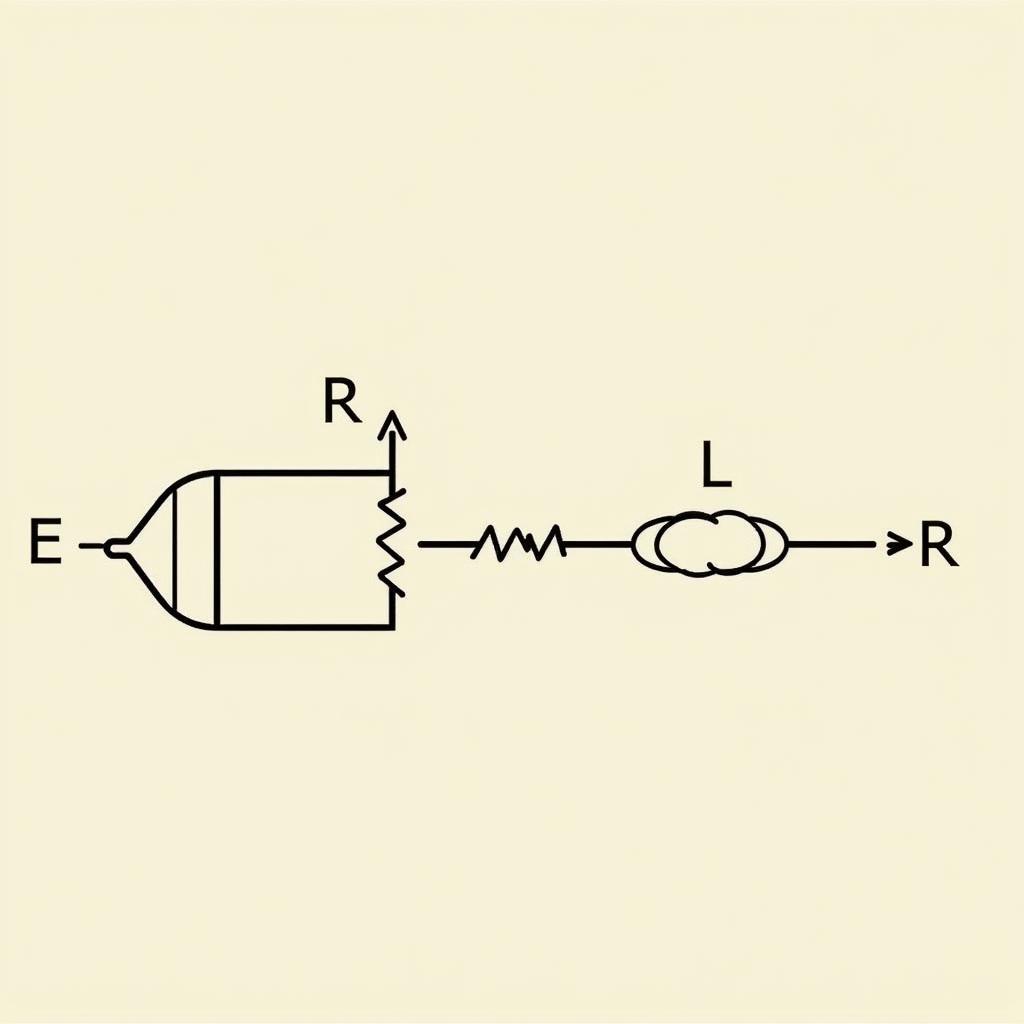Mạch điện RLMạch điện RL

Để giải quyết bài toán mạch RL, chúng ta cần thiết lập phương trình vi phân mô tả sự biến thiên của dòng điện i(t) theo thời gian. Phương trình vi phân được thiết lập dựa trên định luật Kirchhoff về tổng dòng điện tại một nút và định luật Lenz về cảm ứng điện từ:

  • Định luật Kirchhoff: Tổng dòng điện chạy vào một nút bằng tổng dòng điện chạy ra khỏi nút đó.
  • Định luật Lenz: Suất điện động cảm ứng trong cuộn cảm luôn chống lại sự biến thiên của dòng điện chạy qua nó.

Phương trình vi phân của mạch RL:

E = R*i(t) + L*(di(t)/dt)

trong đó:

  • E: Điện áp của nguồn điện (V)
  • R: Điện trở của mạch (Ω)
  • L: Độ tự cảm của cuộn cảm (H)
  • i(t): Dòng điện chạy qua mạch (A)
  • di(t)/dt: Tốc độ biến thiên của dòng điện theo thời gian (A/s)

Các Phương Pháp Giải Bài Toán Mạch RL

Có nhiều phương pháp để giải quyết bài toán mạch RL, bao gồm:

1. Phương Pháp Giả Định Nghiệm

Phương pháp này được áp dụng khi ta đã biết dạng nghiệm của phương trình vi phân. Ví dụ, nếu ta giả định rằng nghiệm của phương trình vi phân là dạng hàm mũ, thì ta có thể thay nghiệm vào phương trình vi phân và giải ra các hệ số của hàm mũ.

2. Phương Pháp Laplace

Phương pháp Laplace là một phương pháp mạnh mẽ để giải các phương trình vi phân tuyến tính. Bằng cách chuyển đổi phương trình vi phân về miền Laplace, ta có thể giải các phương trình đại số, sau đó chuyển đổi ngược trở lại miền thời gian để tìm được nghiệm.

3. Phương Pháp Tích Phân

Phương pháp này sử dụng tích phân để giải phương trình vi phân. Chúng ta có thể tích phân hai vế của phương trình vi phân để tìm ra nghiệm của nó.

4. Phương Pháp Sử Dụng Máy Tính

Các phần mềm chuyên dụng như MATLAB, Mathematica, hoặc PSPICE có thể giúp chúng ta giải quyết các bài toán mạch RL một cách nhanh chóng và chính xác.

Ứng Dụng Của Mạch RL

Mạch RL có nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau như:

1. Bộ Lọc

Mạch RL có thể được sử dụng làm bộ lọc thông thấp (low-pass filter) hoặc bộ lọc thông cao (high-pass filter). Bộ lọc thông thấp cho phép các tín hiệu tần số thấp đi qua và chặn các tín hiệu tần số cao. Ngược lại, bộ lọc thông cao cho phép các tín hiệu tần số cao đi qua và chặn các tín hiệu tần số thấp.

Bộ lọc RLBộ lọc RL

2. Mạch Điều Khiển

Mạch RL có thể được sử dụng để điều khiển dòng điện hoặc điện áp trong các hệ thống điện tử. Ví dụ, mạch RL có thể được sử dụng để điều khiển tốc độ của một động cơ điện một chiều.

3. Mạch Dao Động

Mạch RL có thể được kết hợp với một tụ điện C để tạo thành mạch dao động LC. Mạch dao động LC là một mạch có khả năng tạo ra các tín hiệu sóng sin với tần số riêng của nó.

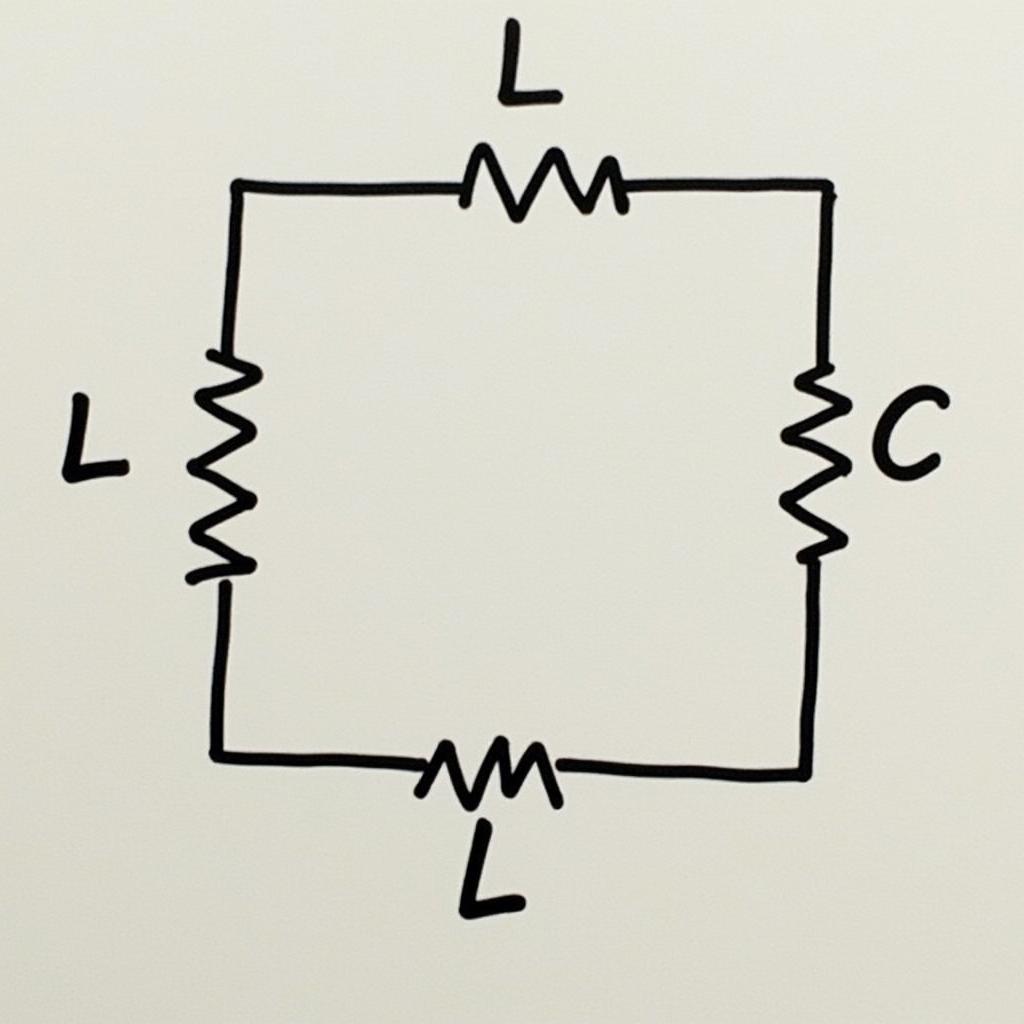Mạch dao động LCMạch dao động LC

Ứng Dụng Thực Tế Của Mạch RL

Mạch RL có nhiều ứng dụng thực tế trong các thiết bị điện tử như:

  • Bộ nguồn: Mạch RL được sử dụng trong các bộ nguồn để lọc và ổn định điện áp đầu ra.
  • Thiết bị âm thanh: Mạch RL được sử dụng trong các hệ thống âm thanh để tạo hiệu ứng âm thanh đặc biệt.
  • Hệ thống điều khiển: Mạch RL được sử dụng trong các hệ thống điều khiển để điều khiển tốc độ, vị trí, hoặc nhiệt độ của các thiết bị.

Lưu Ý Khi Giải Bài Toán Mạch RL

Khi giải quyết các bài toán mạch RL, cần lưu ý một số điểm quan trọng:

  • Dạng nghiệm: Nghiệm của phương trình vi phân mạch RL thường là dạng hàm mũ hoặc hàm sin/cos.
  • Điều kiện ban đầu: Để giải phương trình vi phân, cần biết điều kiện ban đầu của hệ thống, ví dụ như dòng điện ban đầu qua cuộn cảm hoặc điện áp ban đầu trên tụ điện.
  • Chọn phương pháp giải: Chọn phương pháp giải thích hợp cho từng bài toán cụ thể.

Kết Luận

Bài toán mạch RL là một phần quan trọng của môn học Điện tử. Việc hiểu rõ các khái niệm cơ bản và các phương pháp giải quyết bài toán mạch RL là rất cần thiết để thiết kế và ứng dụng các mạch điện tử hiệu quả.

FAQ (Câu Hỏi Thường Gặp)

  1. Làm cách nào để xác định điện áp trên cuộn cảm trong mạch RL?

    Điện áp trên cuộn cảm được tính theo công thức:

     VL = L*(di(t)/dt)

  2. Làm cách nào để xác định năng lượng tích trữ trong cuộn cảm?

    Năng lượng tích trữ trong cuộn cảm được tính theo công thức:

     WL = (1/2)*L*i(t)^2

  3. Mạch RL có thể được sử dụng để tạo ra các sóng vuông hay không?

    Không. Mạch RL tạo ra các sóng sin hoặc các sóng mũ. Để tạo ra sóng vuông, chúng ta có thể sử dụng mạch dao động RC hoặc mạch dao động LC.

  4. Làm cách nào để xác định hằng số thời gian của mạch RL?

    Hằng số thời gian của mạch RL được tính theo công thức:

     τ = L/R

  5. Có thể sử dụng phương pháp tích phân để giải tất cả các bài toán mạch RL hay không?

    Không. Phương pháp tích phân chỉ có thể áp dụng cho một số dạng bài toán mạch RL, trong đó hàm số biểu diễn dòng điện hoặc điện áp có dạng đơn giản.

  6. Làm cách nào để xác định cường độ dòng điện trong mạch RL khi điện áp nguồn là hàm sin?

    Trong trường hợp này, dòng điện trong mạch RL cũng sẽ là hàm sin, nhưng sẽ lệch pha với điện áp nguồn. Pha lệch được xác định bởi hằng số thời gian của mạch.

  7. Có thể sử dụng mạch RL để tạo ra các tín hiệu tần số radio (RF) hay không?

    Có thể. Mạch RL có thể được sử dụng để tạo ra các tín hiệu RF với tần số cao hơn so với các mạch dao động RC. Tuy nhiên, để tạo ra các tín hiệu RF hiệu quả, cần sử dụng các cuộn cảm và tụ điện có độ chính xác cao.

Mô tả các tình huống thường gặp câu hỏi:

  • Khi mới bắt đầu học về mạch RL, sinh viên thường gặp khó khăn trong việc hiểu các khái niệm cơ bản như độ tự cảm, hằng số thời gian, và các phương trình vi phân mô tả mạch.
  • Sinh viên cũng có thể gặp khó khăn trong việc giải các bài toán mạch RL với các hàm số phức tạp hoặc các mạch có nhiều phần tử.
  • Ngoài ra, sinh viên thường băn khoăn về các ứng dụng thực tế của mạch RL.

Gợi ý các câu hỏi khác, bài viết khác có trong web:

  • Bài toán mạch RL với điện áp nguồn là hàm sin
  • Ứng dụng mạch RL trong các thiết bị điện tử
  • Cách giải các bài toán mạch RL phức tạp
  • Cách chọn các thành phần mạch RL phù hợp cho từng ứng dụng

Kêu gọi hành động:

Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.