Bài tập xén hình giải thuật Cohen-Sutherland là một chủ đề quan trọng trong đồ họa máy tính. Giải thuật này giúp xác định phần nào của một đoạn thẳng nằm trong một cửa sổ xem nhất định, cho phép hiển thị hình ảnh hiệu quả hơn. bài tập giải thuật cohen sutherland
Hiểu Về Giải Thuật Cohen-Sutherland
Giải thuật Cohen-Sutherland là một giải thuật xén hình cổ điển, được sử dụng rộng rãi để xác định phần của một đoạn thẳng nằm trong hoặc ngoài một hình chữ nhật được định nghĩa là cửa sổ xem. Giải thuật này hoạt động bằng cách gán mã vùng cho mỗi điểm cuối của đoạn thẳng. Mã vùng này cho biết vị trí của điểm so với cửa sổ xem. Ví dụ, một điểm nằm bên trái cửa sổ xem sẽ có mã vùng khác với điểm nằm bên trong cửa sổ xem.
Bài Tập Xén Hình Giải Thuật Cohen-Sutherland: Các Bước Thực Hiện
-
Xác định mã vùng: Gán mã vùng 4 bit cho mỗi điểm cuối của đoạn thẳng. Mỗi bit đại diện cho một phía của cửa sổ xem (trên, dưới, trái, phải).
-
Kiểm tra tầm nhìn: Nếu cả hai mã vùng đều bằng 0, đoạn thẳng nằm hoàn toàn bên trong cửa sổ xem. Nếu phép AND bit của hai mã vùng khác 0, đoạn thẳng nằm hoàn toàn bên ngoài cửa sổ xem.
-
Xén: Nếu đoạn thẳng không nằm hoàn toàn bên trong hoặc bên ngoài, nó cần được xén. Tìm giao điểm của đoạn thẳng với cạnh của cửa sổ xem và cập nhật tọa độ của điểm cuối.
-
Lặp lại: Lặp lại bước 2 và 3 cho đến khi đoạn thẳng nằm hoàn toàn bên trong hoặc bên ngoài cửa sổ xem.
Ứng Dụng Của Giải Thuật Cohen-Sutherland
Giải thuật Cohen-Sutherland được sử dụng rộng rãi trong đồ họa máy tính, đặc biệt là trong các ứng dụng đồ họa 2D. Nó được dùng để xén hình ảnh trước khi hiển thị, giúp cải thiện hiệu suất và chất lượng hiển thị. bài tập giải thuật cohen sutherland
Ưu điểm của Giải Thuật Cohen-Sutherland
- Đơn giản và dễ thực hiện: Giải thuật này dễ hiểu và triển khai trong code.
- Hiệu quả: Nó khá hiệu quả trong việc xén các đoạn thẳng đơn giản.
Nhược điểm của Giải Thuật Cohen-Sutherland
- Không hiệu quả với đường cong: Giải thuật này chỉ hoạt động với đoạn thẳng, không phải đường cong.
- Có thể cần nhiều phép tính: Trong một số trường hợp, việc xén có thể yêu cầu nhiều phép tính.
Ví dụ Bài Tập Xén Hình Giải Thuật Cohen-Sutherland
Cho một cửa sổ xem với tọa độ (xmin, ymin) và (xmax, ymax). Xét đoạn thẳng với hai điểm cuối P1(x1, y1) và P2(x2, y2). Áp dụng giải thuật Cohen-Sutherland để xác định phần của đoạn thẳng nằm trong cửa sổ xem.
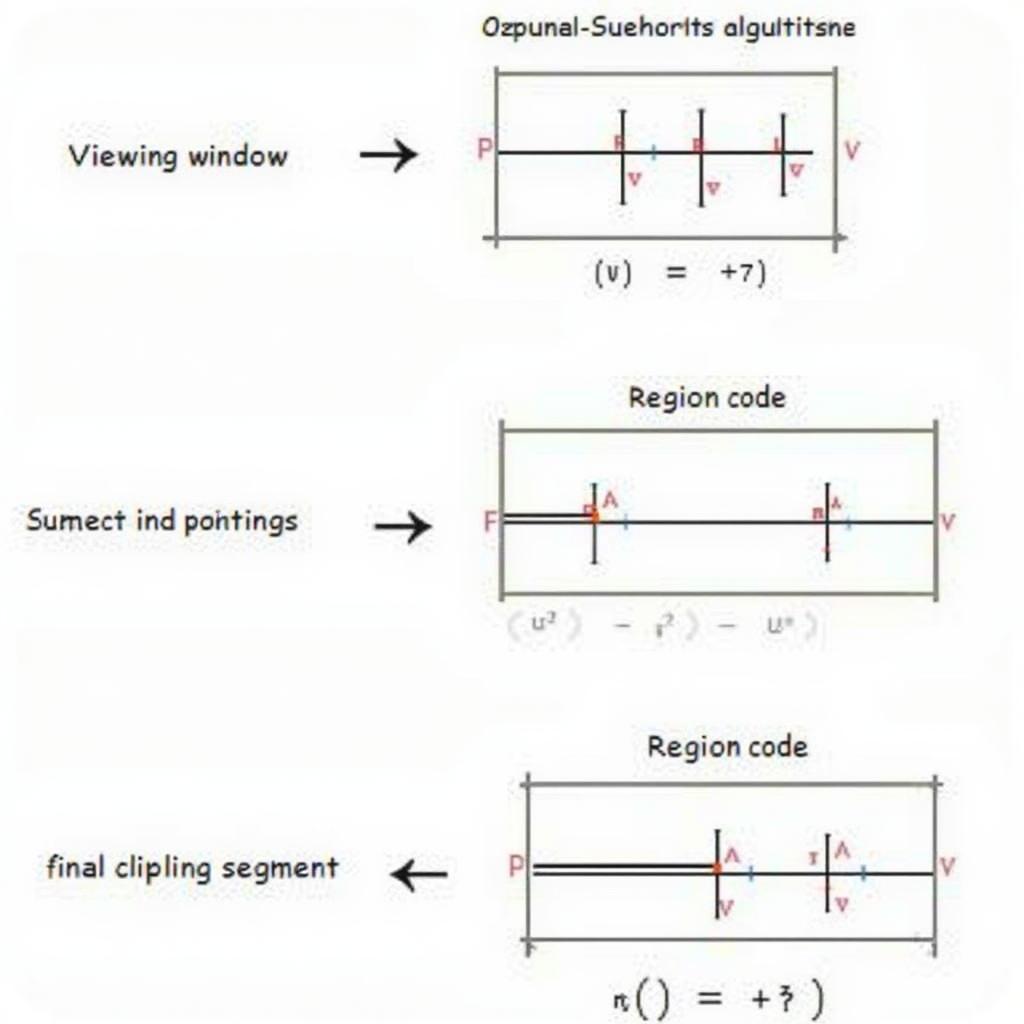Ví dụ bài tập xén hình giải thuật Cohen-Sutherland
Kết luận
Bài tập xén hình giải thuật Cohen-Sutherland là một phần quan trọng của đồ họa máy tính. Hiểu rõ giải thuật này giúp chúng ta xây dựng và tối ưu hóa các ứng dụng đồ họa hiệu quả. bài tập giải thuật cohen sutherland
FAQ
- Giải thuật Cohen-Sutherland là gì?
- Mã vùng trong giải thuật Cohen-Sutherland được tính như thế nào?
- Ưu điểm của giải thuật Cohen-Sutherland là gì?
- Nhược điểm của giải thuật Cohen-Sutherland là gì?
- Giải thuật Cohen-Sutherland được ứng dụng như thế nào trong đồ họa máy tính?
- Có những giải thuật xén hình nào khác ngoài Cohen-Sutherland?
- Làm thế nào để tối ưu hóa việc sử dụng giải thuật Cohen-Sutherland?
Mô tả các tình huống thường gặp câu hỏi.
Người dùng thường thắc mắc về cách tính toán mã vùng và cách xác định giao điểm của đoạn thẳng với cạnh của cửa sổ xem. Ngoài ra, việc so sánh giải thuật Cohen-Sutherland với các giải thuật xén hình khác cũng là một câu hỏi phổ biến.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các giải thuật xén hình khác như Liang-Barsky hoặc Sutherland-Hodgman trên trang web của chúng tôi.