Ứng dụng tích phân có lời giải là một chủ đề quan trọng trong giải tích, giúp người học hiểu sâu hơn về tích phân và cách áp dụng nó vào các bài toán thực tế. Bài viết này sẽ cung cấp cho bạn những kiến thức cần thiết về ứng dụng tích phân, kèm theo các bài tập có lời giải chi tiết để bạn có thể thực hành và nâng cao kỹ năng giải toán.
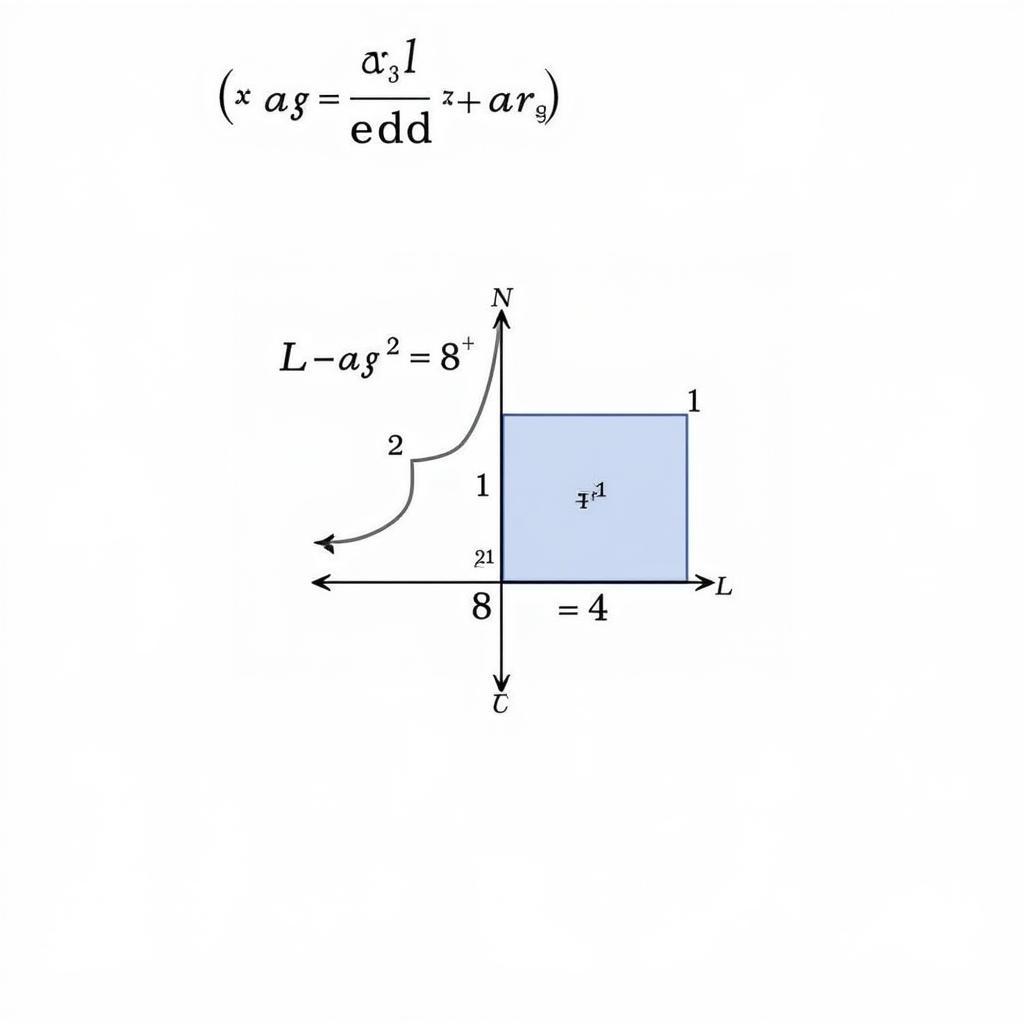 Tính diện tích hình phẳng bằng tích phân
Tính diện tích hình phẳng bằng tích phân
Tìm Diện Tích Hình Phẳng Bằng Tích Phân
Một trong những ứng dụng phổ biến nhất của tích phân là tính diện tích hình phẳng giới hạn bởi các đường cong. Công thức chung để tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành, và hai đường thẳng x = a và x = b là: S = ∫ab |f(x)| dx. Việc nắm vững công thức này sẽ giúp bạn giải quyết nhiều bài toán liên quan đến diện tích. Bạn có thể tìm hiểu thêm về bộ môn giải tích tại bộ môn giải tích.
Ví dụ về bài tập tính diện tích
Bài toán: Tính diện tích hình phẳng giới hạn bởi đường cong y = x² – 4x + 3 và trục hoành.
Lời giải: Đầu tiên, ta tìm giao điểm của đường cong với trục hoành bằng cách giải phương trình x² – 4x + 3 = 0. Nghiệm của phương trình là x = 1 và x = 3. Vậy, diện tích hình phẳng cần tìm là: S = ∫13 |x² – 4x + 3| dx = |-4/3| = 4/3 (đơn vị diện tích).
Tính Thể Tích Vật Thể Tròng
Tích phân cũng được sử dụng để tính thể tích vật thể tròn xoay. Thể tích của vật thể tròn xoay được tạo thành bằng cách quay hình phẳng giới hạn bởi đường cong y = f(x), trục hoành, và hai đường thẳng x = a và x = b quanh trục hoành được tính bằng công thức: V = π∫ab [f(x)]² dx. Tương tự như việc giải các bài tập excel, việc nắm vững các công thức tích phân cũng rất quan trọng. Bạn có thể tham khảo thêm bài tập excel có lời giải nang cao để rèn luyện kỹ năng giải bài tập.
Ví dụ về bài tập tính thể tích
Bài toán: Tính thể tích vật thể tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đường cong y = √x, trục hoành, và đường thẳng x = 4 quanh trục hoành.
Lời giải: Thể tích vật thể tròn xoay được tính bằng: V = π∫04 (√x)² dx = π∫04 x dx = 8π (đơn vị thể tích).
Ứng Dụng Tích Phân Trong Kinh Tế
Tích phân cũng có nhiều ứng dụng trong kinh tế, ví dụ như tính thặng dư tiêu dùng và thặng dư sản xuất. Việc hiểu rõ các ứng dụng này sẽ giúp bạn phân tích các vấn đề kinh tế một cách hiệu quả hơn. Bạn có thể tìm hiểu thêm về các bài tập kinh tế đầu tư tại bài tập môn kinh tế đầu tư có lời giải.
 Ứng dụng tích phân trong kinh tế
Ứng dụng tích phân trong kinh tế
Chuyên gia Nguyễn Văn A, Giảng viên Đại học Kinh tế Quốc dân, chia sẻ: “Việc nắm vững ứng dụng tích phân trong kinh tế là rất quan trọng đối với sinh viên kinh tế.”
Tiến sĩ Trần Thị B, chuyên gia kinh tế, cho biết: “Tích phân giúp chúng ta giải quyết nhiều bài toán thực tế trong kinh tế, đặc biệt là trong lĩnh vực phân tích thị trường.”
Kết luận lại, Bài Tập Về ứng Dụng Tích Phân Có Lời Giải là một phần không thể thiếu trong quá trình học tập giải tích. Hiểu rõ các ứng dụng của tích phân sẽ giúp bạn áp dụng kiến thức vào thực tế một cách hiệu quả. Bạn có thể tìm thêm các bài tập giải tích tại bài tập giải tích 1 có lời giải chi tiết.
FAQ:
- Tích phân là gì?
- Ứng dụng của tích phân trong thực tế là gì?
- Làm thế nào để tính diện tích hình phẳng bằng tích phân?
- Công thức tính thể tích vật thể tròn xoay là gì?
- Tích phân được ứng dụng như thế nào trong kinh tế?
- Tôi có thể tìm thấy các bài tập về ứng dụng tích phân ở đâu?
- Làm thế nào để học tốt tích phân?
Các tình huống thường gặp: Khó khăn trong việc xác định cận tích phân, nhầm lẫn giữa các công thức tính diện tích và thể tích.
Gợi ý các bài viết khác: các phương pháp giải bài tập hóa học 10
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
