Định lý Menelaus và định lý Ceva là hai định lý hình học phẳng kinh điển, đóng vai trò quan trọng trong việc giải quyết các bài toán chứng minh định lý và tính toán trong hình học. Việc nắm vững hai định lý này cùng với việc luyện tập thường xuyên các dạng bài tập sẽ giúp bạn nâng cao khả năng tư duy logic và kỹ năng giải toán hình học của mình.
Định Lý Menelaus và Những Điều Cần Biết
Định nghĩa Định Lý Menelaus
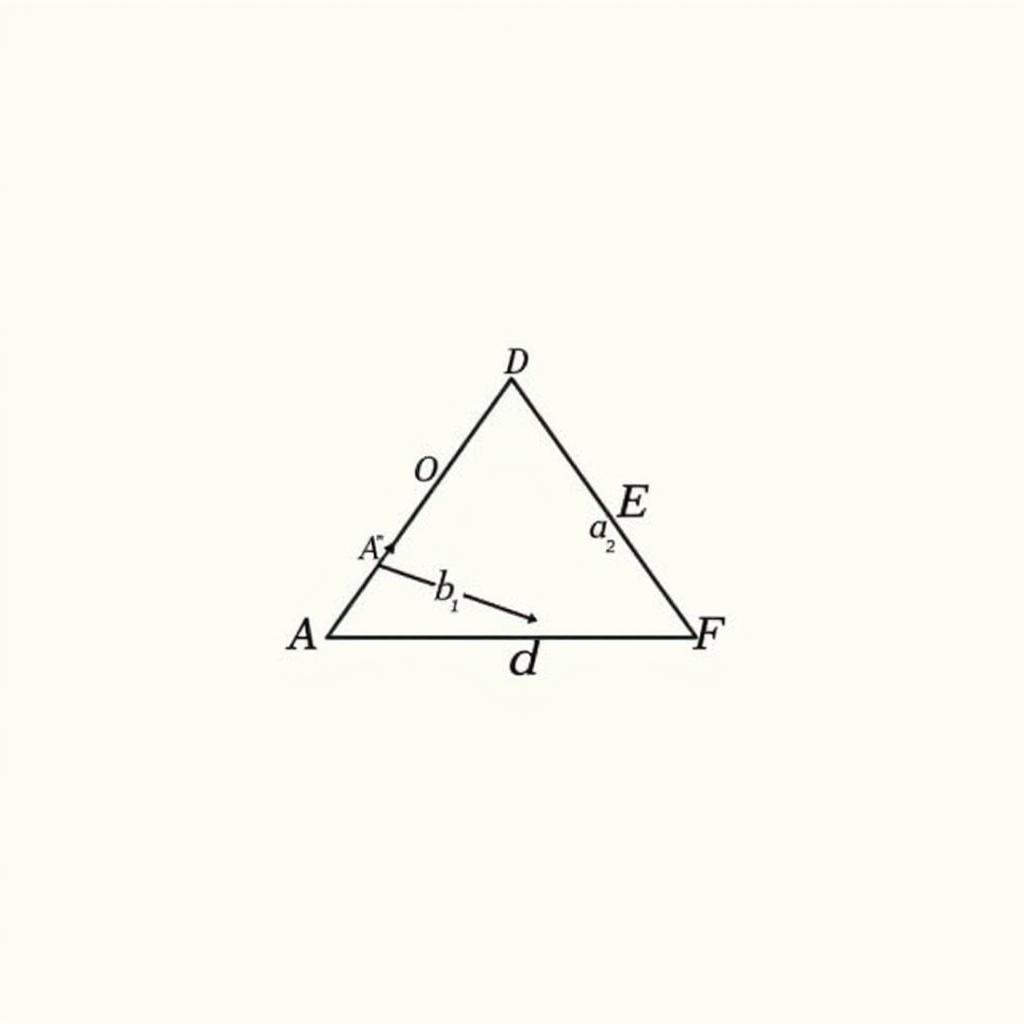 Định lý Menelaus
Định lý Menelaus
Định lý Menelaus được phát biểu như sau: Cho tam giác ABC và một đường thẳng d cắt ba cạnh BC, CA, AB (hoặc đường thẳng chứa chúng) lần lượt tại D, E, F. Khi đó, ba điểm D, E, F thẳng hàng khi và chỉ khi:
(BD/DC) (CE/EA) (AF/FB) = -1
Ý Nghĩa Tỉ Số Trong Định Lý Menelaus
Tỉ số trong định lý Menelaus mang dấu âm hay dương tùy thuộc vào hướng của đoạn thẳng. Ví dụ, BD/DC > 0 nếu BD, DC cùng hướng và BD/DC < 0 nếu BD, DC ngược hướng.
Ứng Dụng Của Định Lý Menelaus
Định lý Menelaus thường được sử dụng để:
- Chứng minh ba điểm thẳng hàng: Bằng cách chứng minh tích các tỉ số bằng -1, ta có thể khẳng định ba điểm đã cho thẳng hàng.
- Chứng minh tỉ số: Ngược lại, nếu biết ba điểm thẳng hàng, ta có thể sử dụng định lý Menelaus để thiết lập mối quan hệ giữa các đoạn thẳng và tính toán tỉ số cần tìm.
Ví Dụ Minh Họa Về Định Lý Menelaus
Cho tam giác ABC, D là trung điểm BC, E là điểm trên AC sao cho AE = 2EC, F là giao điểm của AD và BE. Chứng minh rằng: AF = 3FD.
Lời giải:
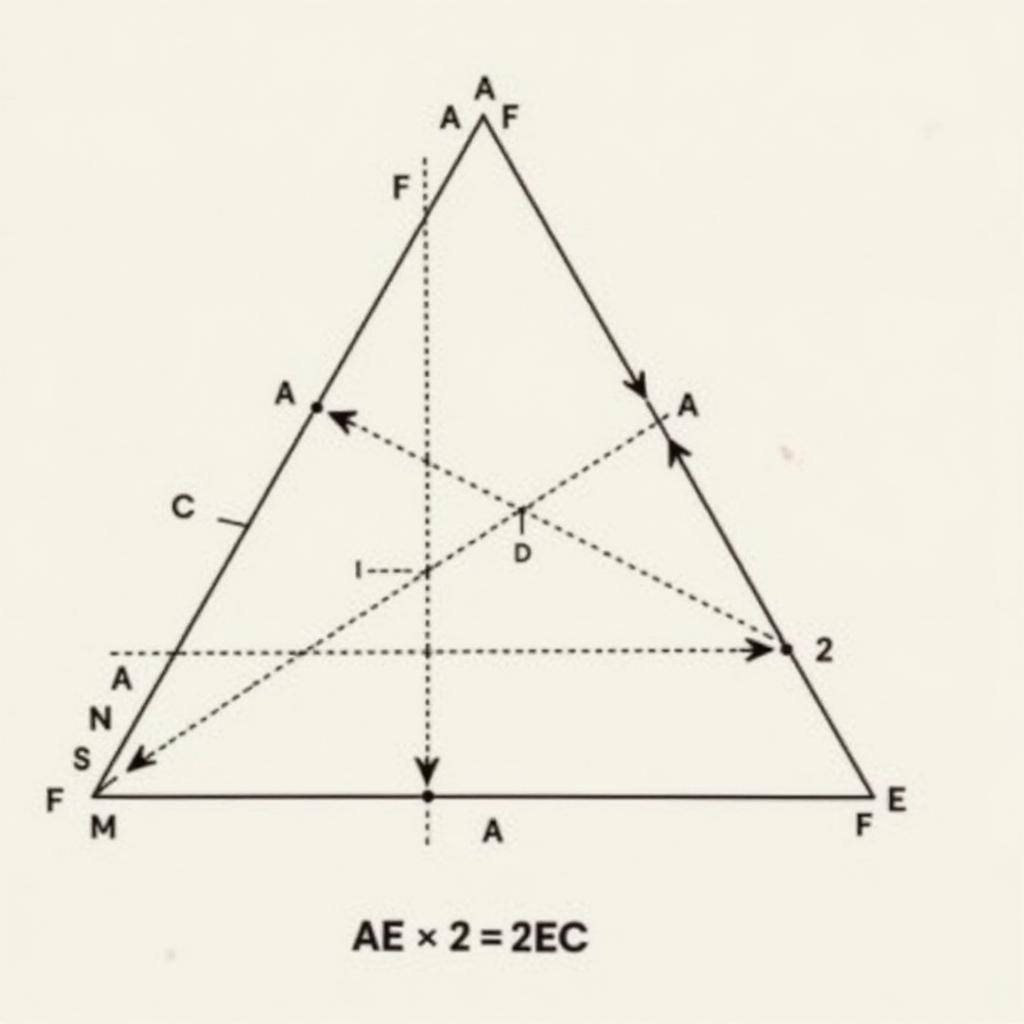 Bài tập minh họa định lý Menelaus
Bài tập minh họa định lý Menelaus
Áp dụng định lý Menelaus cho tam giác ABD với cát tuyến CEF, ta có:
(CD/DB) (BE/EA) (AF/FD) = -1
Vì D là trung điểm BC nên CD/DB = 1.
Vì AE = 2EC nên BE/EA = -1/2 (BE và EA ngược hướng).
Thay vào đẳng thức trên ta được: 1 (-1/2) (AF/FD) = -1
Suy ra: AF/FD = 2 => AF = 2FD.
Định Lý Ceva và Những Điểm Chính
Định nghĩa Định Lý Ceva
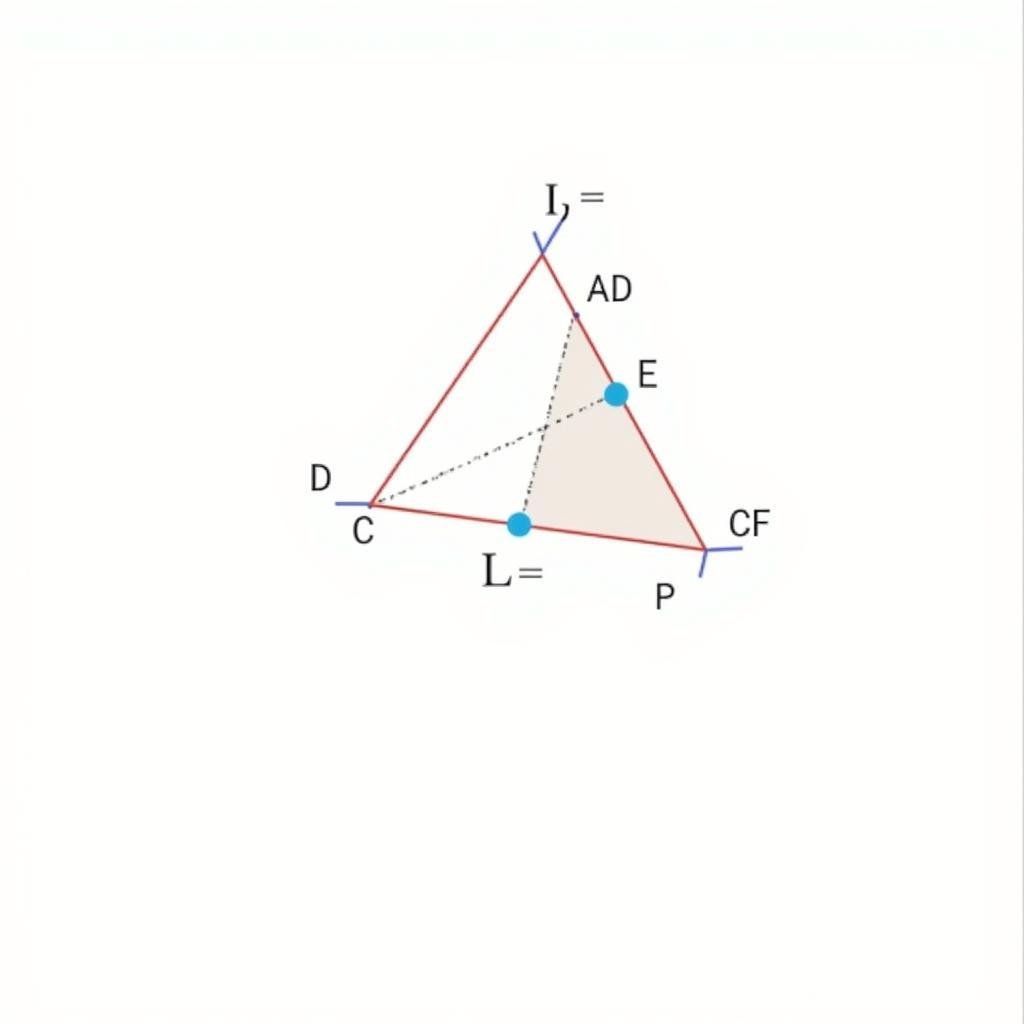 Định lý Ceva
Định lý Ceva
Định lý Ceva được phát biểu như sau: Cho tam giác ABC và ba điểm D, E, F lần lượt nằm trên các cạnh BC, CA, AB. Ba đường thẳng AD, BE, CF đồng quy tại một điểm khi và chỉ khi:
(BD/DC) (CE/EA) (AF/FB) = 1
Điểm Nổi Bật Trong Định Lý Ceva
- Ba đường thẳng AD, BE, CF được gọi là ba đường Cevian của tam giác ABC.
- Điểm đồng quy của ba đường Cevian được gọi là điểm Ceva.
Ứng Dụng Của Định Lý Ceva
Định lý Ceva thường được sử dụng để:
- Chứng minh ba đường thẳng đồng quy: Bằng cách chứng minh tích các tỉ số bằng 1, ta có thể khẳng định ba đường thẳng đã cho đồng quy.
- Xác định vị trí điểm đồng quy: Ngược lại, nếu biết ba đường thẳng đồng quy, ta có thể sử dụng định lý Ceva để xác định vị trí của điểm đồng quy.
Bài Tập Về Định Lý Menelaus và Ceva Có Giải
Bài tập 1:
Cho tam giác ABC, D là trung điểm của BC, E là trung điểm của AD. Đường thẳng BE cắt AC tại F. Chứng minh rằng: AF = 3FC.
Lời giải:
Áp dụng định lý Menelaus cho tam giác ACD với cát tuyến BEF, ta có:
(CD/DB) (BE/EA) (AF/FC) = -1
Vì D là trung điểm BC nên CD/DB = 1.
Vì E là trung điểm AD nên BE/EA = -1 (BE và EA ngược hướng).
Thay vào đẳng thức trên ta được: 1 (-1) (AF/FC) = -1
Suy ra: AF/FC = 1 => AF = FC.
Bài tập 2:
Cho tam giác ABC, AD, BE, CF là ba đường Cevian đồng quy tại điểm P. Biết BD/DC = 2/3 và CE/EA = 3/4. Tính tỉ số AF/FB.
Lời giải:
Áp dụng định lý Ceva cho tam giác ABC với ba đường Cevian AD, BE, CF đồng quy tại P, ta có:
(BD/DC) (CE/EA) (AF/FB) = 1
Thay BD/DC = 2/3 và CE/EA = 3/4 vào đẳng thức trên ta được: (2/3) (3/4) (AF/FB) = 1
Suy ra: AF/FB = 2 => AF = 2FB.
Kết luận
Bài viết đã giới thiệu đến bạn đọc định lý Menelaus và định lý Ceva, cùng với những ví dụ và bài tập có lời giải chi tiết. Hy vọng bài viết “[keyword]” này đã cung cấp cho bạn những kiến thức bổ ích về hai định lý hình học quan trọng này. Việc thường xuyên luyện tập các dạng bài tập và áp dụng linh hoạt hai định lý này sẽ giúp bạn giải quyết hiệu quả các bài toán hình học phẳng.
Câu Hỏi Thường Gặp
1. Sự khác biệt giữa định lý Menelaus và định lý Ceva là gì?
Điểm khác biệt cơ bản nằm ở vị trí của ba điểm D, E, F. Trong định lý Menelaus, ba điểm này nằm trên ba cạnh (hoặc đường thẳng chứa chúng) của tam giác. Trong định lý Ceva, ba điểm này nằm trên ba cạnh của tam giác.
2. Làm thế nào để nhớ công thức của định lý Menelaus và Ceva?
Bạn có thể ghi nhớ công thức một cách dễ dàng bằng cách tưởng tượng đến hình ảnh của tam giác và các đoạn thẳng. Ví dụ, với định lý Menelaus, bạn có thể tưởng tượng đến một đường thẳng cắt ba cạnh tam giác và ghi nhớ tích các tỉ số bằng -1.
3. Ngoài việc chứng minh ba điểm thẳng hàng và ba đường thẳng đồng quy, hai định lý này còn ứng dụng gì khác?
Hai định lý này còn được ứng dụng để chứng minh nhiều định lý hình học khác, ví dụ như định lý Desargues, định lý Pascal…
Bạn cần hỗ trợ? Hãy liên hệ Số Điện Thoại: 02033846993, Email: giaibongda@gmail.com Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
