Bài Tập Quy Hoạch Tuyến Tính Có Lời Giải

Quy hoạch tuyến tính là một mảng toán học quan trọng, thường được ứng dụng để tìm ra giải pháp tối ưu cho các vấn đề trong kinh tế, quản lý và đời sống. Để giúp bạn đọc hiểu rõ hơn về phương pháp giải bài tập quy hoạch tuyến tính, bài viết này sẽ cung cấp những kiến thức từ cơ bản đến nâng cao, kèm theo các ví dụ minh họa cụ thể.

Giải Bài Tập Quy Hoạch Tuyến Tính

Khái Niệm Cơ Bản Về Quy Hoạch Tuyến Tính

Quy hoạch tuyến tính (Linear Programming) là một kỹ thuật toán học được sử dụng để tìm ra giá trị tối ưu (tối đa hoặc tối thiểu) của một hàm mục tiêu tuyến tính, với điều kiện ràng buộc bởi một hệ bất phương trình tuyến tính.

Các thành phần chính của một bài toán quy hoạch tuyến tính bao gồm:

Hàm mục tiêu (Objective Function): Hàm số tuyến tính biểu diễn mục tiêu cần đạt được, ví dụ như tối đa hóa lợi nhuận, tối thiểu hóa chi phí…
Ràng buộc (Constraints): Hệ bất phương trình tuyến tính biểu diễn các giới hạn về nguồn lực, thời gian, công suất…

Các Bước Giải Bài Tập Quy Hoạch Tuyến Tính

Để giải quyết một bài toán quy hoạch tuyến tính, ta có thể áp dụng các phương pháp sau:

Phương pháp hình học: Thích hợp cho bài toán có 2 biến, dựa trên việc biểu diễn miền nghiệm của hệ ràng buộc trên mặt phẳng tọa độ và tìm điểm thuộc miền nghiệm làm cho hàm mục tiêu đạt giá trị tối ưu.
Phương pháp đơn hình (Simplex Method): Phương pháp đại số hiệu quả cho bài toán có nhiều biến, dựa trên việc xét các điểm đỉnh của miền nghiệm để tìm giá trị tối ưu của hàm mục tiêu.

Phương Pháp Đơn Hình Trong Quy Hoạch Tuyến Tính

Ví Dụ Minh Họa

Bài toán: Một công ty sản xuất hai loại sản phẩm A và B. Mỗi sản phẩm A cần 2 giờ gia công và 1 giờ hoàn thiện, mang lại lợi nhuận là 3 triệu đồng. Mỗi sản phẩm B cần 1 giờ gia công và 3 giờ hoàn thiện, mang lại lợi nhuận là 4 triệu đồng. Biết rằng tổng thời gian gia công không quá 8 giờ và tổng thời gian hoàn thiện không quá 9 giờ. Hỏi công ty nên sản xuất bao nhiêu sản phẩm mỗi loại để đạt lợi nhuận tối đa?

Lời giải:

Bước 1: Lập mô hình toán học

Gọi x là số sản phẩm A, y là số sản phẩm B cần sản xuất. Ta có mô hình toán học như sau:

Hàm mục tiêu: F(x, y) = 3x + 4y (tối đa hóa lợi nhuận)
Ràng buộc:
- 2x + y ≤ 8 (giới hạn thời gian gia công)
- x + 3y ≤ 9 (giới hạn thời gian hoàn thiện)
- x ≥ 0, y ≥ 0 (điều kiện không âm)

Bước 2: Giải bài toán bằng phương pháp hình học

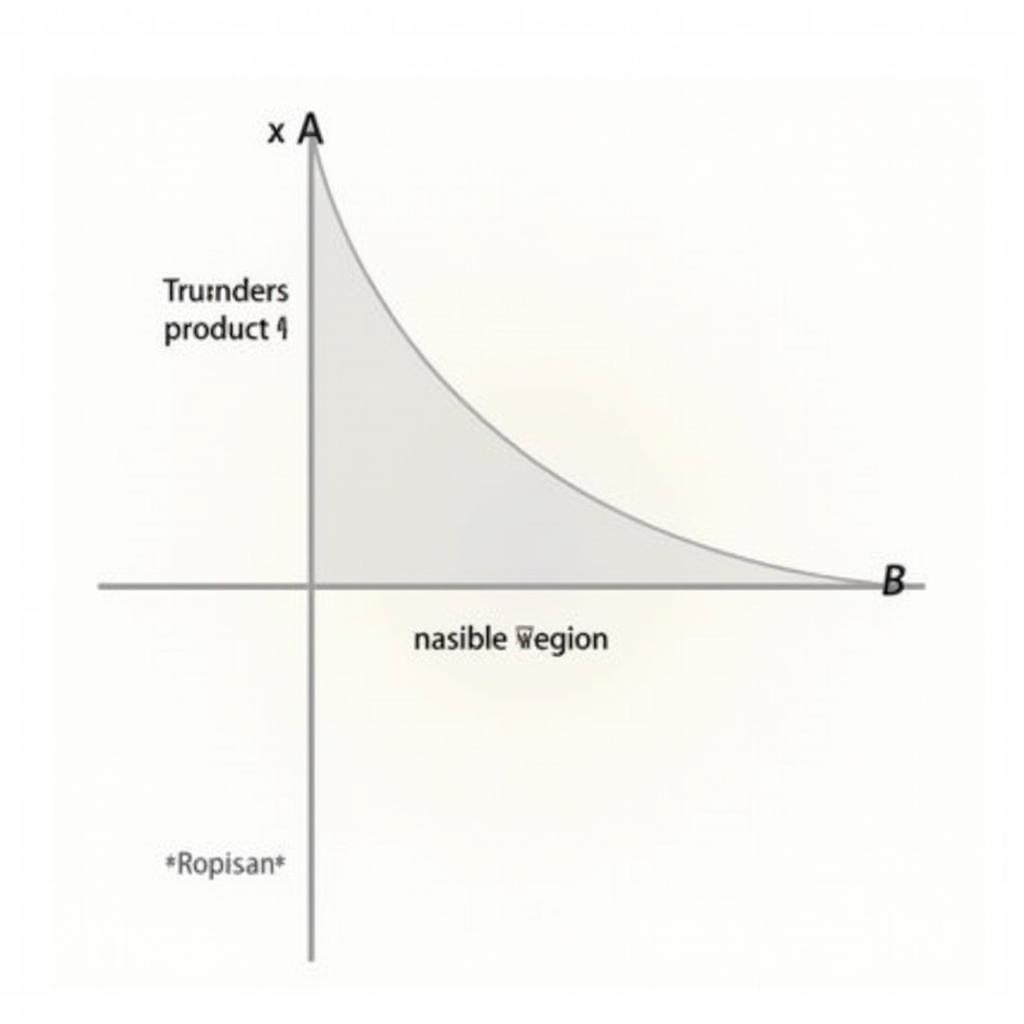
Biểu Diễn Bài Toán Quy Hoạch Tuyến Tính Trên Đồ Thị

Vẽ các đường thẳng biểu diễn các ràng buộc trên hệ trục tọa độ Oxy. Miền nghiệm của bài toán là phần mặt phẳng bị giới hạn bởi các đường thẳng này và các trục tọa độ.

Tìm tọa độ các điểm giao nhau của các đường thẳng, ta được các điểm (0, 0), (0, 3), (4, 0), (3, 2).

Tính giá trị của hàm mục tiêu F(x, y) tại các điểm này, ta được:

F(0, 0) = 0
F(0, 3) = 12
F(4, 0) = 12
F(3, 2) = 17

Vậy, để đạt lợi nhuận tối đa (17 triệu đồng), công ty nên sản xuất 3 sản phẩm A và 2 sản phẩm B.

Kết Luận

Bài tập quy hoạch tuyến tính có lời giải là một phần quan trọng giúp người học nắm vững kiến thức và ứng dụng vào thực tế. Hy vọng bài viết này đã cung cấp cho bạn đọc những kiến thức bổ ích về quy hoạch tuyến tính và cách giải các bài toán liên quan.

FAQ

1. Quy hoạch tuyến tính được ứng dụng trong những lĩnh vực nào?

Quy hoạch tuyến tính được ứng dụng rộng rãi trong nhiều lĩnh vực như:

Kinh tế: Tối ưu hóa sản xuất, phân bổ nguồn lực, quản lý kho bãi, đầu tư tài chính…
Quản lý: Lập kế hoạch sản xuất, phân công lao động, tối ưu hóa chuỗi cung ứng…
Giao thông vận tải: Lập lịch trình vận chuyển, tối ưu hóa tuyến đường…

2. Có những phần mềm nào hỗ trợ giải bài toán quy hoạch tuyến tính?

Có nhiều phần mềm hỗ trợ giải bài toán quy hoạch tuyến tính, phổ biến nhất là:

Microsoft Excel Solver: Công cụ tích hợp sẵn trong Microsoft Excel, dễ sử dụng cho bài toán quy mô nhỏ.
Lindo: Phần mềm chuyên dụng cho quy hoạch tuyến tính và phi tuyến, mạnh mẽ và linh hoạt.
GAMS: Ngôn ngữ lập trình toán học và hệ thống tối ưu hóa, phù hợp cho bài toán quy mô lớn và phức tạp.

3. Bài toán quy hoạch tuyến tính có những hạn chế nào?

Mặc dù có nhiều ưu điểm, quy hoạch tuyến tính vẫn có một số hạn chế:

Giả định tuyến tính: Không phải lúc nào mối quan hệ giữa các biến cũng tuyến tính trong thực tế.
Không tính đến yếu tố bất định: Bài toán quy hoạch tuyến tính thường giả định các thông số đầu vào là cố định, trong khi thực tế có thể thay đổi.

4. Ngoài phương pháp hình học và đơn hình, còn phương pháp nào khác để giải bài toán quy hoạch tuyến tính?

Ngoài hai phương pháp trên, còn có các phương pháp khác như:

Phương pháp điểm trong (Interior Point Method): Hiệu quả cho bài toán quy mô lớn.
Phương pháp phân rã (Decomposition Method): Phù hợp cho bài toán có cấu trúc đặc biệt.

5. Làm thế nào để học tốt quy hoạch tuyến tính?

Để học tốt quy hoạch tuyến tính, bạn nên:

Nắm vững kiến thức cơ bản về đại số tuyến tính, hệ phương trình, bất phương trình…
Luyện tập giải nhiều bài tập từ đơn giản đến phức tạp.
Tham khảo các tài liệu, sách vở, khóa học uy tín.

Gợi ý các bài viết khác

Bạn đọc có thể tham khảo thêm các bài viết liên quan trên trang web Giải Bóng:

Liên Hệ

Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.