Phương trình lượng giác là một phần quan trọng trong chương trình toán học phổ thông, đồng thời cũng là kiến thức nền tảng cho nhiều ngành học và lĩnh vực khác. Để giúp bạn đọc nắm vững kiến thức và tự tin giải quyết các bài tập phương trình lượng giác, bài viết này sẽ cung cấp những kiến thức trọng tâm, phương pháp giải bài tập hiệu quả và những lời giải chi tiết, dễ hiểu.
Nắm Vững Kiến Thức Căn Bản Về Phương Trình Lượng Giác
Trước khi bắt tay vào giải bài tập, việc đầu tiên bạn cần làm là nắm chắc những kiến thức căn bản về phương trình lượng giác.
Các Loại Phương Trình Lượng Giác Thường Gặp
Có rất nhiều dạng phương trình lượng giác khác nhau, tuy nhiên trong chương trình phổ thông, bạn sẽ thường gặp một số loại cơ bản sau:
-
Phương trình bậc nhất đối với một hàm số lượng giác: Đây là dạng phương trình có dạng a.sinx + b.cosx = c (hoặc a.tanx + b = 0, a.cotx + b = 0), trong đó a, b, c là các số thực và a, b không đồng thời bằng 0.
-
Phương trình bậc hai đối với một hàm số lượng giác: Dạng phương trình này có dạng a.sin2x + b.sinx.cosx + c.cos2x = d (hoặc a.tan2x + b.tanx + c = 0, a.cot2x + b.cotx + c = 0), trong đó a, b, c, d là các số thực và a, b, c không đồng thời bằng 0.
-
Phương trình bậc nhất đối với sinx và cosx: Loại phương trình này có dạng a.sinx + b.cosx = c, với a, b, c là các số thực và a, b không đồng thời bằng 0.
-
Phương trình dạng asinx + bcosx = c: Đây là dạng phương trình thường gặp, có thể giải bằng nhiều cách khác nhau như sử dụng công thức cộng, đặt ẩn phụ, hoặc sử dụng phương pháp hình học.
Công Thức Lượng Giác Cần Ghi Nhớ
Để giải quyết các bài tập phương trình lượng giác, bạn cần ghi nhớ một số công thức lượng giác cơ bản như:
- Công thức cộng: sin(a ± b), cos(a ± b), tan(a ± b)
- Công thức nhân đôi: sin2a, cos2a, tan2a
- Công thức hạ bậc: sin2a, cos2a
- Công thức biến đổi tích thành tổng, tổng thành tích.
Công thức lượng giác
Phương Pháp Giải Bài Tập Phương Trình Lượng Giác
Mỗi dạng phương trình lượng giác sẽ có những phương pháp giải quyết riêng. Dưới đây là một số phương pháp thường được sử dụng:
Phương pháp dùng công thức lượng giác
Phương pháp này áp dụng cho những bài toán có thể sử dụng trực tiếp các công thức lượng giác cơ bản để biến đổi phương trình về dạng đơn giản hơn.
Ví dụ: Giải phương trình sin2x – cosx = 0
Ta có: sin2x = 2sinx.cosx
Thay vào phương trình ban đầu, ta được: 2sinx.cosx – cosx = 0
<=> cosx(2sinx – 1) = 0
<=> cosx = 0 hoặc sinx = 1/2
Từ đó, ta dễ dàng tìm được nghiệm của phương trình.
Phương pháp đặt ẩn phụ
Với những phương trình phức tạp hơn, ta có thể sử dụng phương pháp đặt ẩn phụ để đưa phương trình về dạng đơn giản đã biết cách giải.
Ví dụ: Giải phương trình sin2x + 3sinx.cosx + 2cos2x = 0
Nhận thấy phương trình có thể viết lại dưới dạng: (sinx + cosx)(sinx + 2cosx) = 0
Đặt t = sinx + cosx, ta được: t(t + cosx) = 0
Giải phương trình này ta tìm được t, sau đó thay lại để tìm x.
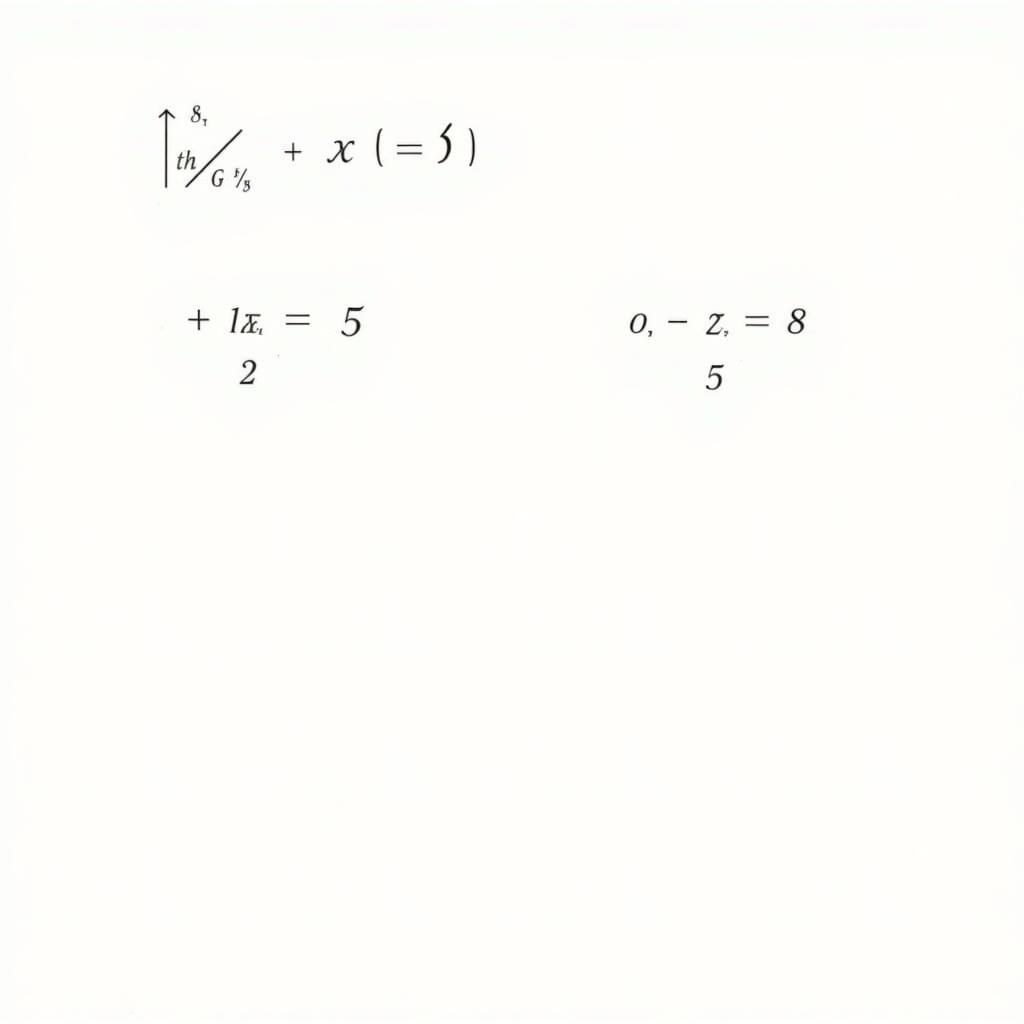Phương pháp đặt ẩn phụ
Phương pháp sử dụng đường tròn lượng giác
Đường tròn lượng giác là công cụ hữu ích giúp ta hình dung và giải quyết các bài toán lượng giác một cách trực quan.
Ví dụ: Tìm nghiệm của phương trình sinx = 1/2 trên đoạn [0, 2π].
Ta biểu diễn góc x trên đường tròn lượng giác. Điểm M biểu diễn góc x sẽ có tung độ bằng 1/2. Từ đó, ta dễ dàng xác định được hai góc x thỏa mãn là π/6 và 5π/6.
Bài Tập Phương Trình Lượng Giác Có Lời Giải
Để giúp bạn đọc củng cố kiến thức, dưới đây là một số Bài Tập Phương Trình Lượng Giác Có Lời Giải chi tiết:
Bài tập 1: Giải phương trình 2sinx – √3 = 0
Lời giải:
Ta có: 2sinx – √3 = 0
<=> sinx = √3/2
<=> x = π/3 + k2π hoặc x = 2π/3 + k2π (k ∈ Z)
Bài tập 2: Giải phương trình cos2x – 3cosx + 2 = 0
Lời giải:
Đặt t = cosx, ta được: t2 – 3t + 2 = 0
<=> (t – 1)(t – 2) = 0
<=> t = 1 hoặc t = 2
- Nếu t = 1 thì cosx = 1 <=> x = k2π (k ∈ Z)
- Nếu t = 2 (loại vì |cosx| ≤ 1)
Vậy nghiệm của phương trình là x = k2π (k ∈ Z)
Bài tập 3: Giải phương trình tanx + cotx = 2
Lời giải:
Điều kiện: sin2x ≠ 0 <=> x ≠ kπ/2 (k ∈ Z)
Ta có: tanx + cotx = 2
<=> sinx/cosx + cosx/sinx = 2
<=> (sin2x + cos2x)/(sinx.cosx) = 2
<=> 1/(sinx.cosx) = 2
<=> sin2x = 1
<=> 2x = π/2 + k2π
<=> x = π/4 + kπ (k ∈ Z) (thỏa mãn điều kiện)
Vậy nghiệm của phương trình là x = π/4 + kπ (k ∈ Z)
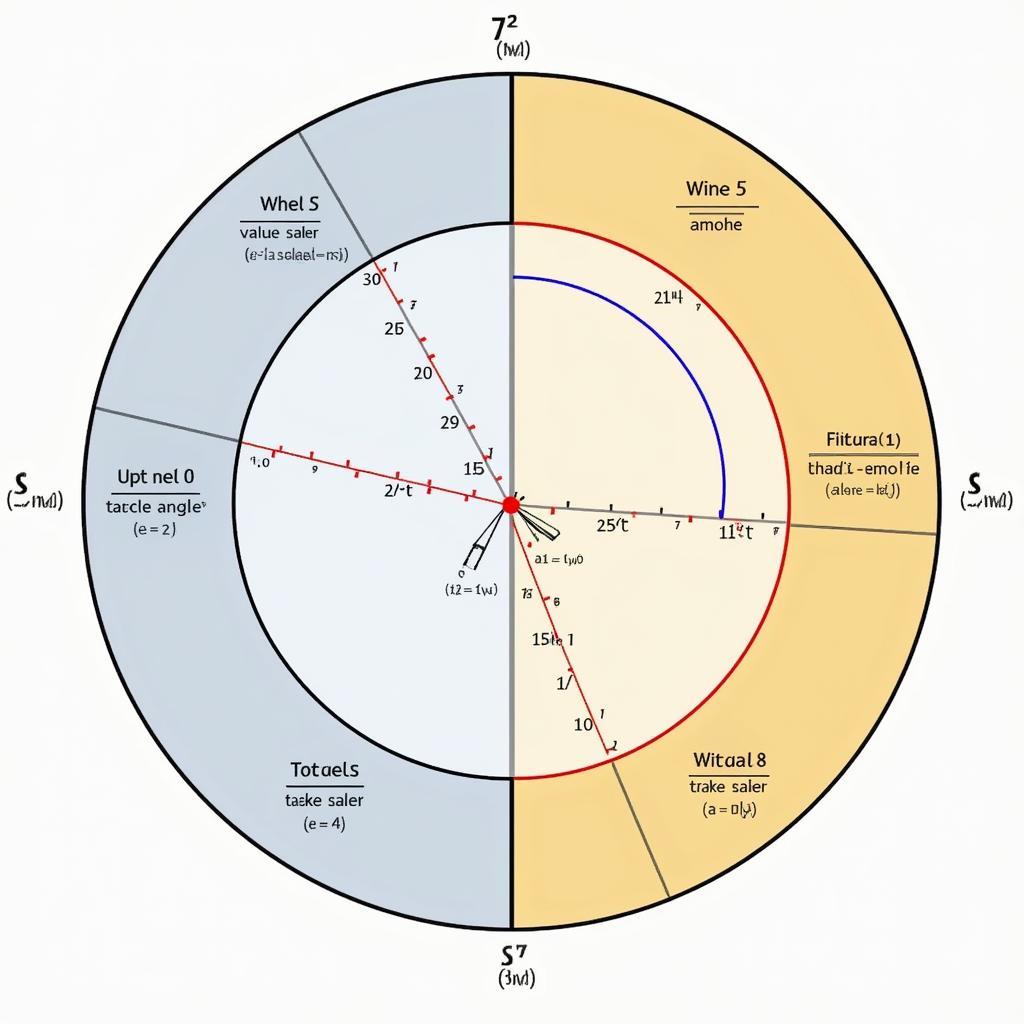Đường tròn lượng giác
Kết Luận
Bài viết đã cung cấp cho bạn đọc những kiến thức cơ bản, phương pháp giải và bài tập phương trình lượng giác có lời giải chi tiết. Hy vọng rằng bài viết này sẽ giúp bạn đọc tự tin hơn trong việc giải quyết các bài toán liên quan đến phương trình lượng giác.
Để nâng cao kỹ năng giải bài tập, bạn đọc nên thường xuyên luyện tập giải các bài tập với mức độ khó tăng dần. Bên cạnh đó, việc tham khảo các tài liệu tham khảo, sách giáo khoa và tìm kiếm sự hỗ trợ từ giáo viên, bạn bè cũng là điều rất cần thiết.
FAQ
1. Làm thế nào để xác định được dạng của phương trình lượng giác?
Để xác định dạng của phương trình lượng giác, bạn cần quan sát kỹ cấu trúc của phương trình, xem xét bậc của hàm số lượng giác, mối quan hệ giữa các hàm số lượng giác trong phương trình.
2. Khi nào nên sử dụng phương pháp đặt ẩn phụ?
Bạn nên sử dụng phương pháp đặt ẩn phụ khi nhận thấy có thể nhóm hoặc biến đổi phương trình ban đầu về dạng phương trình đơn giản hơn, đã biết cách giải.
3. Đường tròn lượng giác có ứng dụng gì trong giải bài tập phương trình lượng giác?
Đường tròn lượng giác giúp ta hình dung và xác định được vị trí của góc, giá trị của các hàm số lượng giác một cách trực quan, từ đó hỗ trợ việc tìm nghiệm của phương trình.
4. Làm thế nào để ghi nhớ các công thức lượng giác một cách hiệu quả?
Bạn có thể ghi nhớ các công thức lượng giác bằng cách viết ra giấy nhiều lần, kết hợp với việc luyện tập giải bài tập thường xuyên.
5. Ngoài các phương pháp đã nêu, còn có phương pháp nào khác để giải phương trình lượng giác không?
Ngoài các phương pháp đã nêu, còn có thể sử dụng phương pháp đồ thị, phương pháp sử dụng máy tính cầm tay để giải phương trình lượng giác.
Bạn có thể quan tâm đến:
Liên hệ
Nếu bạn cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.