Hồi quy tuyến tính là một phương pháp thống kê được sử dụng rộng rãi để mô hình hóa mối quan hệ giữa một biến phụ thuộc và một hoặc nhiều biến độc lập. Bài viết này cung cấp cái nhìn chi tiết về Bài Tập Hồi Quy Tuyến Tính Có Lời Giải, giúp bạn nắm vững kiến thức và áp dụng hiệu quả vào thực tế.
Ví dụ bài tập hồi quy tuyến tính
Hồi Quy Tuyến Tính Là Gì?
Hồi quy tuyến tính tìm kiếm một hàm tuyến tính có thể biểu diễn tốt nhất mối quan hệ giữa biến phụ thuộc (thường được ký hiệu là Y) và một hoặc nhiều biến độc lập (thường được ký hiệu là X). Mối quan hệ này được biểu diễn bằng một phương trình đường thẳng, với các hệ số cho biết mức độ ảnh hưởng của các biến độc lập đến biến phụ thuộc.
Các Bước Thực Hiện Bài Tập Hồi Quy Tuyến Tính
Để giải quyết bài tập hồi quy tuyến tính, bạn có thể tuân theo các bước sau:
- Xác định biến phụ thuộc và biến độc lập: Xác định biến nào bạn muốn dự đoán (biến phụ thuộc) và biến nào có thể ảnh hưởng đến biến đó (biến độc lập).
- Thu thập dữ liệu: Thu thập dữ liệu về biến phụ thuộc và biến độc lập.
- Vẽ biểu đồ phân tán: Vẽ biểu đồ phân tán để trực quan hóa mối quan hệ giữa các biến.
- Xác định phương trình hồi quy: Sử dụng phương pháp bình phương tối thiểu để tìm phương trình đường thẳng phù hợp nhất với dữ liệu.
- Kiểm tra ý nghĩa thống kê: Sử dụng các kiểm định thống kê để đánh giá ý nghĩa của mô hình hồi quy.
- Đánh giá mô hình: Đánh giá độ chính xác của mô hình bằng cách sử dụng các chỉ số như R-bình phương.
- Dự đoán: Sử dụng phương trình hồi quy để dự đoán giá trị của biến phụ thuộc dựa trên các giá trị cho trước của biến độc lập.
Ví Dụ Bài Tập Hồi Quy Tuyến Tính Có Lời Giải
Bài toán: Một công ty muốn dự đoán doanh thu bán hàng dựa trên chi phí quảng cáo. Họ đã thu thập dữ liệu về chi phí quảng cáo (triệu đồng) và doanh thu bán hàng (tỷ đồng) trong 10 tháng qua như sau:
| Chi Phí Quảng Cáo (X) | Doanh Thu Bán Hàng (Y) |
|---|---|
| 2 | 5 |
| 3 | 7 |
| 4 | 8 |
| 5 | 10 |
| 6 | 11 |
| 7 | 13 |
| 8 | 14 |
| 9 | 16 |
| 10 | 18 |
| 11 | 19 |
Yêu cầu:
- Xây dựng phương trình hồi quy tuyến tính thể hiện mối quan hệ giữa chi phí quảng cáo và doanh thu bán hàng.
- Dự đoán doanh thu bán hàng nếu chi phí quảng cáo là 12 triệu đồng.
Lời giải:
-
Xây dựng phương trình hồi quy:
Sử dụng phương pháp bình phương tối thiểu, ta có thể tính toán được phương trình hồi quy tuyến tính như sau:
Y = 1.67X + 1.67Trong đó:
- Y là doanh thu bán hàng (tỷ đồng)
- X là chi phí quảng cáo (triệu đồng)
-
Dự đoán doanh thu bán hàng:
Thay X = 12 vào phương trình hồi quy, ta có:
Y = 1.67 * 12 + 1.67 = 21.71Vậy, doanh thu bán hàng dự kiến là 21.71 tỷ đồng nếu chi phí quảng cáo là 12 triệu đồng.
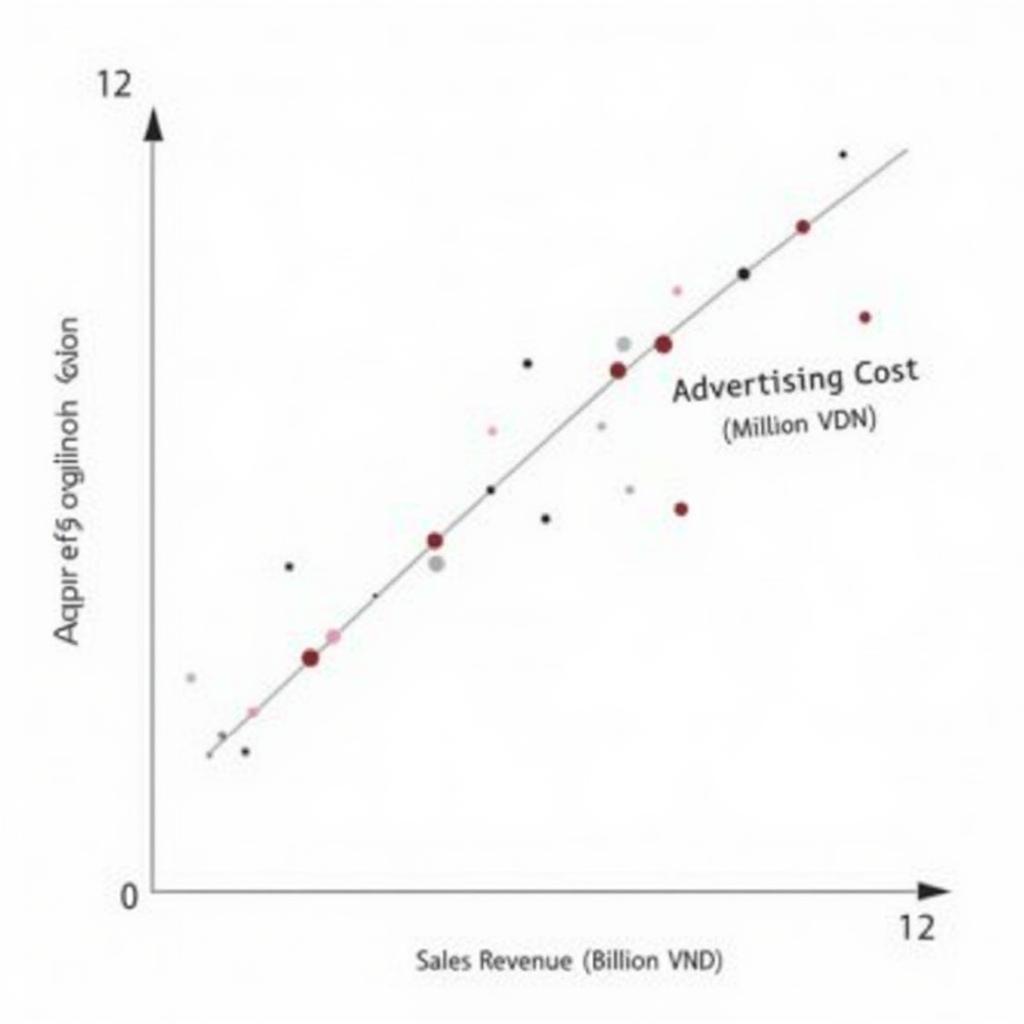Biểu đồ phân tán và đường hồi quy tuyến tính
Ứng Dụng Của Hồi Quy Tuyến Tính
Hồi quy tuyến tính được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
- Kinh doanh: Dự đoán doanh thu, chi phí, lợi nhuận.
- Tài chính: Dự đoán giá cổ phiếu, lãi suất.
- Marketing: Đo lường hiệu quả của chiến dịch quảng cáo.
- Y tế: Dự đoán nguy cơ mắc bệnh, hiệu quả điều trị.
Kết Luận
Bài viết đã cung cấp cái nhìn tổng quan về bài tập hồi quy tuyến tính có lời giải, bao gồm khái niệm, các bước thực hiện, ví dụ minh họa và ứng dụng. Hy vọng bài viết này hữu ích cho bạn trong việc nắm vững kiến thức và vận dụng hồi quy tuyến tính vào thực tế.
Bạn muốn tìm hiểu thêm về các phương pháp thống kê khác như sáng kiến kinh nghiệm lớp 2 đạt giải hoặc bộ giải pháp quản lý doanh nghiệp trực tuyến? Hãy truy cập website Giải Bóng để có thêm thông tin chi tiết.
Câu Hỏi Thường Gặp
1. Hồi quy tuyến tính có thể sử dụng cho biến phân loại được không?
Không, hồi quy tuyến tính chỉ phù hợp cho biến phụ thuộc là biến liên tục. Đối với biến phụ thuộc là biến phân loại, bạn có thể sử dụng hồi quy logistic.
2. Làm thế nào để đánh giá độ chính xác của mô hình hồi quy tuyến tính?
Bạn có thể sử dụng các chỉ số như R-bình phương, RMSE, MAE để đánh giá độ chính xác của mô hình.
3. R-bình phương là gì?
R-bình phương là thước đo thống kê cho biết tỷ lệ biến động của biến phụ thuộc được giải thích bởi mô hình hồi quy.
4. Hồi quy tuyến tính có nhạy cảm với outlier không?
Có, hồi quy tuyến tính nhạy cảm với outlier. Do đó, việc xử lý outlier là cần thiết trước khi xây dựng mô hình.
5. Có bao nhiêu loại hồi quy tuyến tính?
Có hai loại hồi quy tuyến tính chính: hồi quy tuyến tính đơn biến và hồi quy tuyến tính đa biến.
Bạn Cần Hỗ Trợ?
Liên hệ ngay với chúng tôi:
- Số Điện Thoại: 02033846993
- Email: [email protected]
- Địa Chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam.
Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.