Bài Tập Hàm Cấu Trúc Rời Rạc Có Lời Giải là tài liệu quan trọng giúp sinh viên nắm vững kiến thức về cấu trúc rời rạc. Việc luyện giải các bài tập này không chỉ củng cố lý thuyết mà còn rèn luyện tư duy logic, phân tích và giải quyết vấn đề.
Tìm Hiểu Về Hàm Cấu Trúc Rời Rạc
Hàm cấu trúc rời rạc là một ánh xạ giữa các tập rời rạc. Chúng ta thường gặp các dạng bài tập về hàm đơn ánh, toàn ánh, song ánh, cũng như các phép toán trên hàm như hợp thành hàm và hàm ngược. Hiểu rõ các khái niệm này là nền tảng để giải quyết các bài toán phức tạp hơn.
Các Loại Bài Tập Hàm Cấu Trúc Rời Rạc Thường Gặp
Bài Tập Về Tính Chất Của Hàm
Các bài tập loại này thường yêu cầu chứng minh một hàm là đơn ánh, toàn ánh hay song ánh. Đôi khi, đề bài sẽ cho một hàm và yêu cầu tìm điều kiện để hàm đó thỏa mãn một tính chất nào đó.
Bài Tập Về Phép Toán Trên Hàm
Phép toán trên hàm bao gồm hợp thành hàm và hàm ngược. Bài tập thường yêu cầu tìm hàm hợp thành của hai hoặc nhiều hàm, hoặc tìm hàm ngược của một hàm cho trước.
Bài Tập Ứng Dụng
Các bài tập ứng dụng hàm cấu trúc rời rạc thường xuất hiện trong các lĩnh vực như khoa học máy tính, mật mã học và lý thuyết đồ thị. Ví dụ, hàm băm (hash function) trong khoa học máy tính là một ứng dụng của hàm cấu trúc rời rạc.
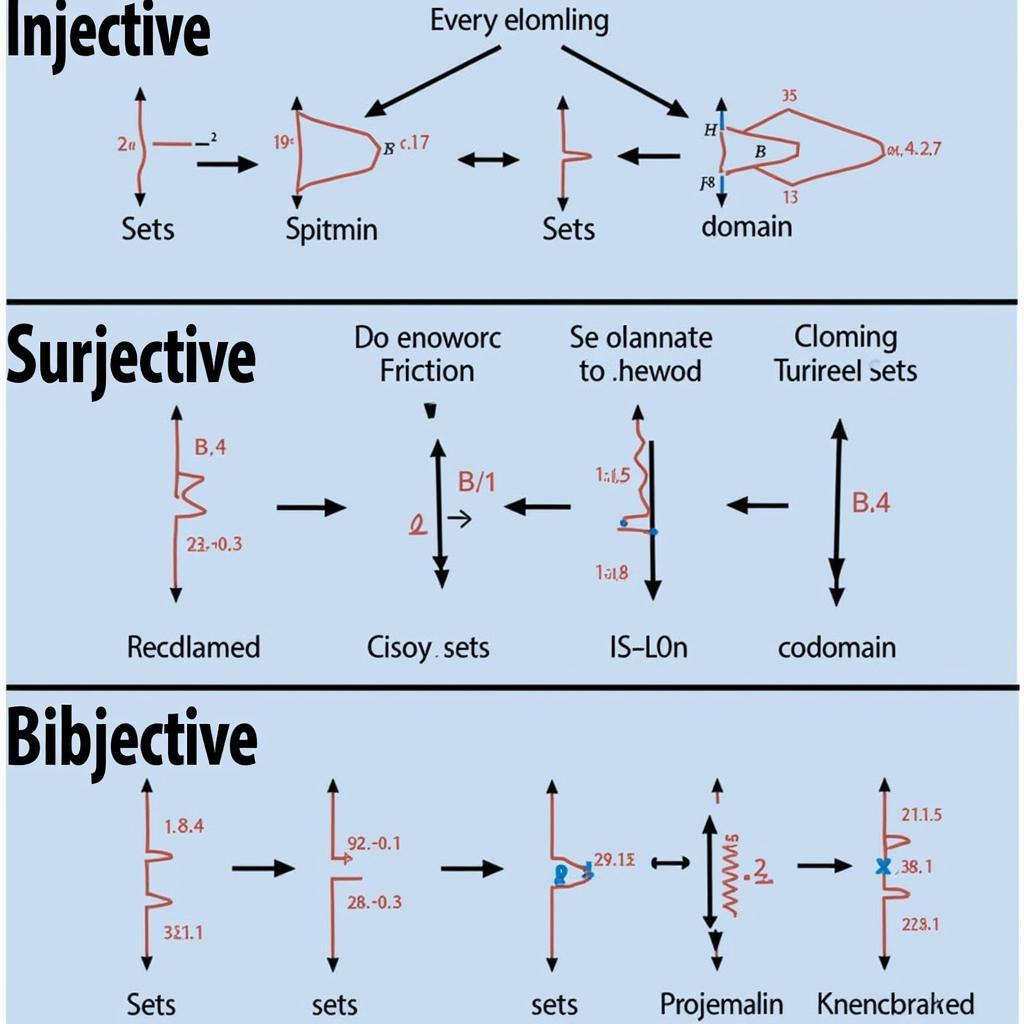 Bài tập hàm cấu trúc rời rạc về tính chất của hàm
Bài tập hàm cấu trúc rời rạc về tính chất của hàm
Phương Pháp Giải Bài Tập Hàm Cấu Trúc Rời Rạc
Để giải quyết các bài tập hàm cấu trúc rời rạc, cần nắm vững định nghĩa và tính chất của từng loại hàm. Việc vẽ biểu đồ minh họa cũng rất hữu ích để hình dung bài toán. Ngoài ra, cần luyện tập thường xuyên để nâng cao kỹ năng giải quyết vấn đề.
Xác Định Tính Chất Của Hàm
Để xác định một hàm là đơn ánh, ta cần chứng minh mỗi phần tử trong tập đích chỉ được ánh xạ tới bởi tối đa một phần tử trong tập nguồn. Đối với toàn ánh, ta cần chứng minh mọi phần tử trong tập đích đều được ánh xạ tới bởi ít nhất một phần tử trong tập nguồn. Một hàm là song ánh khi nó vừa là đơn ánh vừa là toàn ánh.
Tìm Hàm Hợp Thành
Để tìm hàm hợp thành của hai hàm f và g, ta áp dụng công thức (f o g)(x) = f(g(x)). Tức là, ta thay x trong hàm f bằng g(x).
Tìm Hàm Ngược
Để tìm hàm ngược của một hàm f, ta cần đổi chỗ x và y trong phương trình y = f(x), sau đó giải phương trình theo y.
Ví Dụ Bài Tập Hàm Cấu Trúc Rời Rạc Có Lời Giải
Cho hàm f: A -> B được định nghĩa bởi f(x) = 2x + 1, với A = {1, 2, 3} và B = {3, 5, 7}. Chứng minh f là song ánh.
Lời giải:
- Đơn ánh: Giả sử f(x1) = f(x2). Ta có 2×1 + 1 = 2×2 + 1 => x1 = x2. Vậy f là đơn ánh.
- Toàn ánh: Với mỗi y thuộc B, ta cần tìm x thuộc A sao cho f(x) = y. Ta có 2x + 1 = y => x = (y – 1)/2. Vì y thuộc {3, 5, 7}, nên x thuộc {1, 2, 3} = A. Vậy f là toàn ánh.
Vì f vừa là đơn ánh vừa là toàn ánh, nên f là song ánh.
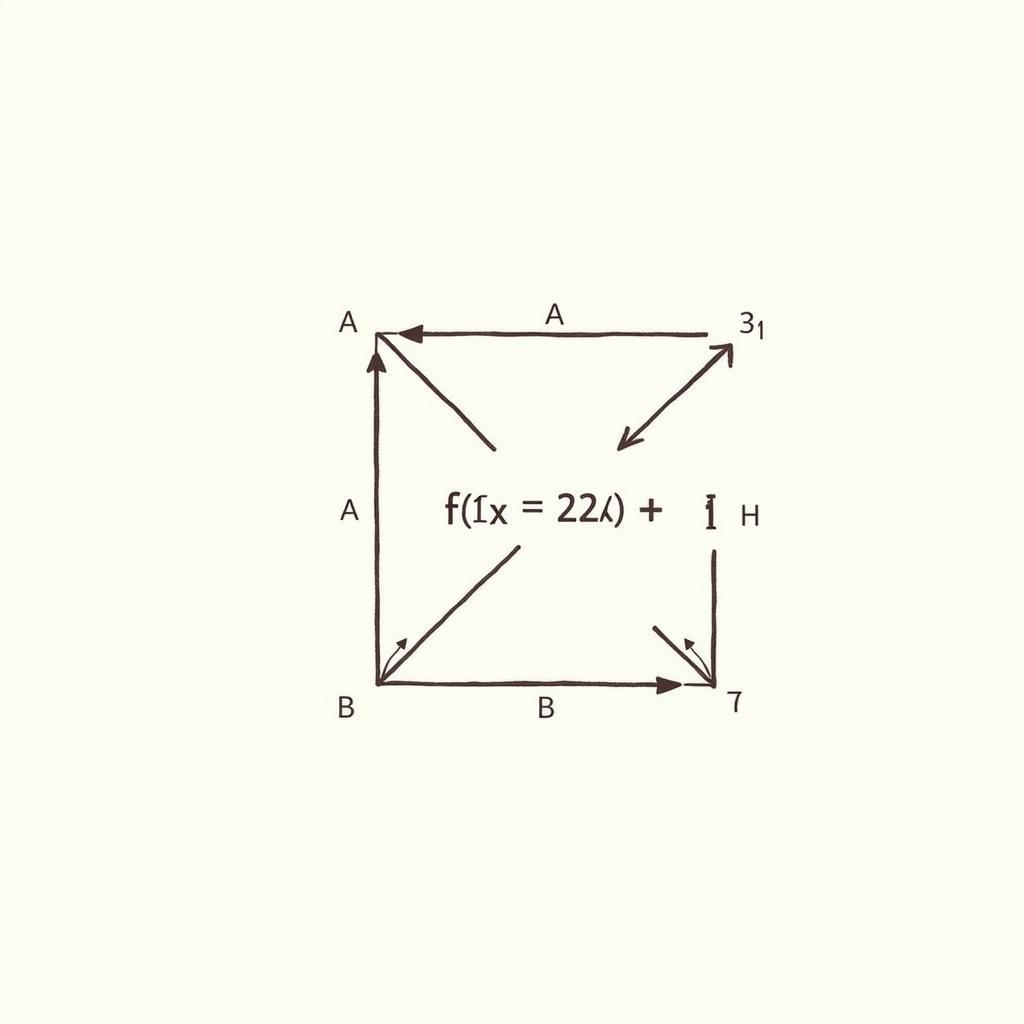 Ví dụ bài tập hàm cấu trúc rời rạc có lời giải
Ví dụ bài tập hàm cấu trúc rời rạc có lời giải
Kết luận
Bài tập hàm cấu trúc rời rạc có lời giải là công cụ hữu ích để nắm vững kiến thức về cấu trúc rời rạc. Việc luyện tập thường xuyên và áp dụng đúng phương pháp sẽ giúp bạn giải quyết các bài toán một cách hiệu quả.
Mô tả các tình huống thường gặp câu hỏi.
Sinh viên thường gặp khó khăn trong việc chứng minh tính chất của hàm, đặc biệt là khi phải tìm điều kiện để hàm thỏa mãn một tính chất nào đó. Việc hiểu rõ định nghĩa và áp dụng các kỹ thuật chứng minh là rất quan trọng.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các chủ đề liên quan như quan hệ, đồ thị, và đại số Boolean trên website “Giải Bóng”.
