Phương trình bậc 2 là một khái niệm toán học cơ bản xuất hiện từ bậc trung học cơ sở. Việc giải phương trình bậc 2 là nền tảng để giải quyết các bài toán phức tạp hơn ở bậc học cao hơn và trong thực tế. Bài viết này cung cấp cho bạn kiến thức đầy đủ về cách giải phương trình bậc 2 kèm theo các bài tập có đáp án để bạn luyện tập.
Phương Trình Bậc 2 Là Gì?
Phương trình bậc 2 là phương trình có dạng ax² + bx + c = 0, trong đó:
- a, b, c là các hệ số, a ≠ 0
- x là ẩn số
Cách Giải Phương Trình Bậc 2
Có nhiều cách để giải phương trình bậc 2, phổ biến nhất là sử dụng công thức nghiệm và phương pháp phân tích thành nhân tử.
1. Công Thức Nghiệm
Bước 1: Xác định các hệ số a, b, c.
Bước 2: Tính delta (∆): ∆ = b² – 4ac
Bước 3: Xét dấu của delta:
- ∆ > 0: Phương trình có hai nghiệm phân biệt:
- x₁ = (-b + √∆) / 2a
- x₂ = (-b – √∆) / 2a
- ∆ = 0: Phương trình có nghiệm kép: x₁ = x₂ = -b / 2a
- ∆ < 0: Phương trình vô nghiệm.
2. Phân Tích Thành Nhân Tử
Phương pháp này áp dụng khi phương trình bậc 2 có thể phân tích thành nhân tử có dạng (mx + n)(px + q) = 0.
Bước 1: Phân tích vế trái của phương trình thành nhân tử.
Bước 2: Giải hai phương trình bậc nhất:
- mx + n = 0
- px + q = 0
Lưu ý: Không phải phương trình bậc 2 nào cũng có thể phân tích thành nhân tử.
 Ví dụ giải phương trình bậc 2 bằng công thức nghiệm
Ví dụ giải phương trình bậc 2 bằng công thức nghiệm
Bài Tập Giải Phương Trình Bậc 2 Có Đáp Án
Bài 1: Giải phương trình: x² – 5x + 6 = 0
Lời giải:
- a = 1, b = -5, c = 6
- ∆ = (-5)² – 4 1 6 = 1
- ∆ > 0, phương trình có hai nghiệm phân biệt:
- x₁ = (5 + √1) / 2 * 1 = 3
- x₂ = (5 – √1) / 2 * 1 = 2
Bài 2: Giải phương trình: 2x² + 4x + 2 = 0
Lời giải:
- a = 2, b = 4, c = 2
- ∆ = 4² – 4 2 2 = 0
- ∆ = 0, phương trình có nghiệm kép: x₁ = x₂ = -4 / 2 * 2 = -1
Bài 3: Giải phương trình: x² + x + 1 = 0
Lời giải:
- a = 1, b = 1, c = 1
- ∆ = 1² – 4 1 1 = -3
- ∆ < 0, phương trình vô nghiệm.
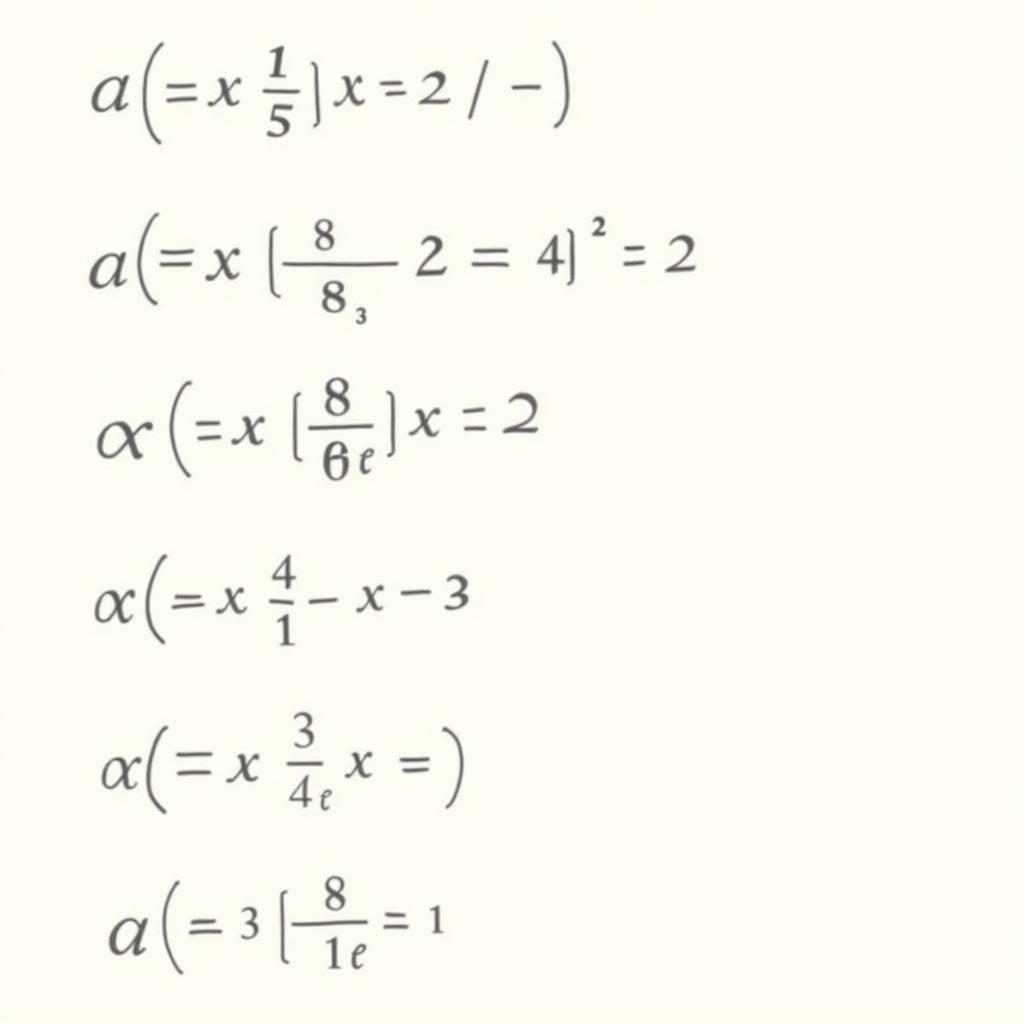 Ví dụ giải phương trình bậc 2 bằng phương pháp phân tích thành nhân tử
Ví dụ giải phương trình bậc 2 bằng phương pháp phân tích thành nhân tử
Kết Luận
Bài viết đã cung cấp kiến thức cơ bản về phương trình bậc 2 và cách giải phương trình bậc 2 bằng công thức nghiệm và phương pháp phân tích thành nhân tử. Hy vọng qua các Bài Tập Giải Phương Trình Bậc 2 Có đáp án, bạn đã nắm vững kiến thức và có thể áp dụng để giải quyết các bài toán liên quan.
FAQ
1. Khi nào nên sử dụng công thức nghiệm, khi nào nên phân tích thành nhân tử?
Nên ưu tiên phân tích thành nhân tử khi nhận thấy phương trình có thể phân tích dễ dàng. Nếu gặp khó khăn trong việc phân tích, hãy sử dụng công thức nghiệm.
2. Phương trình bậc 2 có ứng dụng gì trong thực tế?
Phương trình bậc 2 được ứng dụng trong nhiều lĩnh vực như vật lý, kỹ thuật, kinh tế… Ví dụ, tính toán quỹ đạo của vật thể, thiết kế cầu đường, dự đoán lợi nhuận…
3. Làm thế nào để nhớ công thức nghiệm?
Có nhiều cách để ghi nhớ công thức nghiệm, ví dụ như học thuộc lòng, viết ra giấy nhiều lần, liên tưởng đến hình ảnh…
 Ứng dụng thực tế của phương trình bậc 2
Ứng dụng thực tế của phương trình bậc 2
Bạn cần hỗ trợ?
Liên hệ với chúng tôi:
- Số Điện Thoại: 02033846993
- Email: [email protected]
- Địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam.
Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
