Chương 2 toán học lớp 11 là bước khởi đầu cho hành trình khám phá thế giới toán học nâng cao, với những kiến thức mới đầy thử thách và bổ ích. Để chinh phục những bài tập trong chương này, bạn cần nắm vững các lý thuyết, công thức và phương pháp giải bài tập. Bài viết này sẽ giúp bạn làm chủ chương 2 toán 11 một cách dễ dàng với những bài tập có lời giải chi tiết và phương pháp giải hiệu quả.
Các chủ đề chính trong chương 2 toán 11
Chương 2 toán 11 bao gồm các chủ đề chính như:
- Hàm số bậc nhất: Nghiên cứu các tính chất, đồ thị và ứng dụng của hàm số bậc nhất.
- Hàm số bậc hai: Khám phá các tính chất, đồ thị và ứng dụng của hàm số bậc hai.
- Hàm số mũ và hàm số logarit: Tìm hiểu về định nghĩa, tính chất, đồ thị và ứng dụng của hàm số mũ và hàm số logarit.
- Phương trình mũ và phương trình logarit: Nắm vững cách giải các phương trình mũ và phương trình logarit.
- Bất phương trình mũ và bất phương trình logarit: Ứng dụng kiến thức về hàm số mũ và hàm số logarit để giải bất phương trình.
Các bài tập chương 2 toán 11 có lời giải chi tiết
Bài tập 1: Hàm số bậc nhất
Bài toán: Cho hàm số $y = 2x + 1$.
- a) Vẽ đồ thị hàm số.
- b) Tìm tọa độ giao điểm của đồ thị hàm số với hai trục tọa độ.
- c) Tìm giá trị của $x$ để hàm số nhận giá trị bằng $5$.
Lời giải:
- a) Đồ thị hàm số $y = 2x + 1$ là một đường thẳng đi qua hai điểm $A(0; 1)$ và $B(-1/2; 0)$.
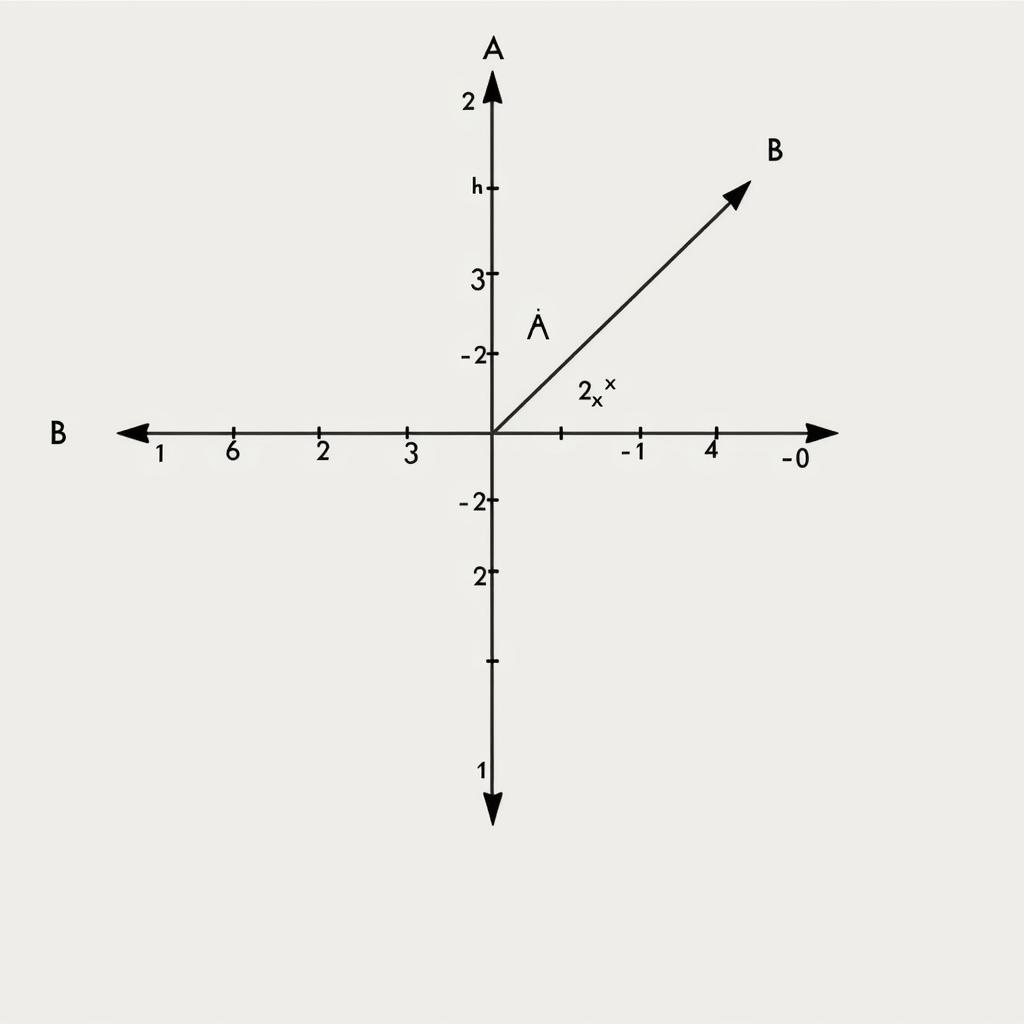
- b) Giao điểm của đồ thị hàm số với trục $Oy$ là điểm $(0; 1)$. Giao điểm của đồ thị hàm số với trục $Ox$ là điểm $(-1/2; 0)$.
- c) Thay $y = 5$ vào phương trình $y = 2x + 1$, ta được: $5 = 2x + 1$. Giải phương trình, ta được $x = 2$.
Bài tập 2: Hàm số bậc hai
Bài toán: Cho hàm số $y = -x^2 + 4x – 3$.
- a) Vẽ đồ thị hàm số.
- b) Tìm tọa độ đỉnh của parabol.
- c) Tìm khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
- a) Đồ thị hàm số $y = -x^2 + 4x – 3$ là một parabol có đỉnh tại điểm $I(2; 1)$ và trục đối xứng là đường thẳng $x = 2$.

- b) Tọa độ đỉnh của parabol là $I(2; 1)$.
- c) Hàm số đồng biến trên khoảng $(-infty; 2)$ và nghịch biến trên khoảng $(2; +infty)$.
Bài tập 3: Hàm số mũ và hàm số logarit
Bài toán: Cho hàm số $y = 2^x$.
- a) Vẽ đồ thị hàm số.
- b) Tìm tập xác định, tập giá trị của hàm số.
- c) Tính giá trị của hàm số tại $x = 2$.
Lời giải:
- a) Đồ thị hàm số $y = 2^x$ là một đường cong đi qua điểm $(0; 1)$ và có tiệm cận ngang là trục $Ox$.
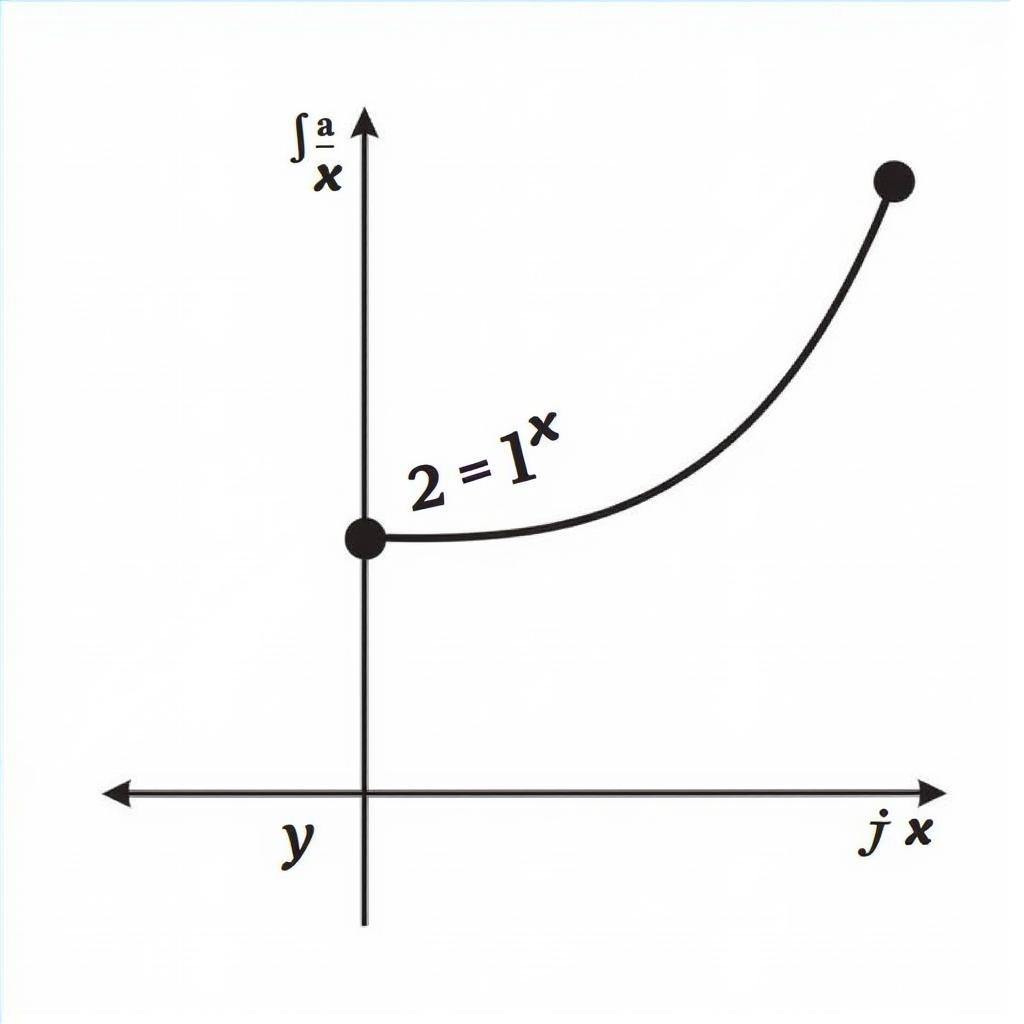
- b) Tập xác định của hàm số là $D = R$. Tập giá trị của hàm số là $T = (0; +infty)$.
- c) $y(2) = 2^2 = 4$.
Bài tập 4: Phương trình mũ và phương trình logarit
Bài toán: Giải phương trình $2^{x+1} – 3.2^x + 2 = 0$.
Lời giải:
Chia cả hai vế của phương trình cho $2^x$, ta được:
$2 – 3 + frac{2}{2^x} = 0$
$Leftrightarrow frac{2}{2^x} = 1$
$Leftrightarrow 2^x = 2$
$Leftrightarrow x = 1$.
Vậy phương trình có nghiệm $x = 1$.
Bài tập 5: Bất phương trình mũ và bất phương trình logarit
Bài toán: Giải bất phương trình $log_2(x+1) > 1$.
Lời giải:
Điều kiện xác định: $x + 1 > 0 Leftrightarrow x > -1$.
$log_2(x+1) > 1 Leftrightarrow x + 1 > 2 Leftrightarrow x > 1$.
Kết hợp với điều kiện xác định, ta được tập nghiệm của bất phương trình là $S = (1; +infty)$.
Kết luận
Chương 2 toán 11 là một phần quan trọng trong hành trình chinh phục kiến thức toán học của bạn. Hiểu rõ các lý thuyết, công thức và phương pháp giải bài tập là chìa khóa để bạn thành công trong chương này. Hãy dành thời gian để luyện tập và làm những bài tập có lời giải chi tiết để củng cố kiến thức và nâng cao kỹ năng giải toán của mình. Chúc bạn học tập hiệu quả!
FAQ
- Câu hỏi 1: Chương 2 toán 11 có khó không?
- Trả lời: Chương 2 toán 11 có độ khó vừa phải, nhưng đòi hỏi bạn cần nắm vững kiến thức cơ bản và có kỹ năng tư duy logic.
- Câu hỏi 2: Làm sao để học tốt chương 2 toán 11?
- Trả lời: Bạn nên học theo lộ trình, từ dễ đến khó, chú trọng vào các lý thuyết và công thức, làm nhiều bài tập và tham khảo thêm các tài liệu hỗ trợ.
- Câu hỏi 3: Có tài liệu nào hỗ trợ học chương 2 toán 11 hiệu quả?
- Trả lời: Bạn có thể tìm kiếm tài liệu trên internet, sách giáo khoa, sách bài tập hoặc tham gia các khóa học online.
- Câu hỏi 4: Có thể tham khảo lời giải chi tiết của các bài tập chương 2 toán 11 ở đâu?
- Trả lời: Bạn có thể tìm kiếm trên các trang web giáo dục, diễn đàn toán học hoặc các sách bài tập có lời giải.
- Câu hỏi 5: Nên làm gì khi gặp khó khăn trong việc học chương 2 toán 11?
- Trả lời: Bạn nên tìm kiếm sự trợ giúp từ giáo viên, bạn bè hoặc các chuyên gia toán học.
Gợi ý:
- Bạn có thể tham khảo thêm các bài viết khác trên website Giaibong.com để củng cố kiến thức về toán học.
- Nếu bạn cần hỗ trợ thêm về chương 2 toán 11, hãy liên hệ với chúng tôi qua số điện thoại: 02033846993, email: [email protected] hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi luôn sẵn sàng hỗ trợ bạn 24/7.
