Bài Tập Các Cổng Logic Cơ Bản Có Lời Giải là chìa khóa để hiểu sâu hơn về điện tử số và thiết kế mạch logic. Việc thực hành với các bài tập này sẽ giúp bạn nắm vững cách hoạt động của các cổng AND, OR, NOT, NAND, NOR, XOR và XNOR.
Các Cổng Logic Cơ Bản và Bảng Chân Lý
Cổng AND
Cổng AND chỉ cho ra kết quả 1 (TRUE) khi tất cả các đầu vào đều là 1. Ngược lại, nếu có bất kỳ đầu vào nào là 0 (FALSE), kết quả sẽ là 0.
Cổng OR
Cổng OR cho ra kết quả 1 khi có ít nhất một đầu vào là 1. Chỉ khi tất cả đầu vào đều là 0 thì kết quả mới là 0.
Cổng NOT
Cổng NOT đảo ngược giá trị đầu vào. Nếu đầu vào là 1, kết quả là 0 và ngược lại.
Cổng NAND (NOT AND)
Cổng NAND là sự kết hợp của cổng AND và NOT. Nó cho ra kết quả ngược lại với cổng AND.
Cổng NOR (NOT OR)
Cổng NOR là sự kết hợp của cổng OR và NOT. Nó cho ra kết quả ngược lại với cổng OR.
Cổng XOR (Exclusive OR)
Cổng XOR chỉ cho ra kết quả 1 khi có một và chỉ một đầu vào là 1. Nếu cả hai đầu vào giống nhau (cùng là 0 hoặc cùng là 1), kết quả sẽ là 0.
Cổng XNOR (Exclusive NOR)
Cổng XNOR là sự kết hợp của cổng XOR và NOT. Nó cho ra kết quả ngược lại với cổng XOR.
Bài Tập Cổng Logic Cơ Bản và Lời Giải
Bài Tập 1: Thiết kế mạch logic cho hàm F = AB + C
Hãy thiết kế mạch logic sử dụng các cổng cơ bản để thực hiện hàm logic F = AB + C.
- Lời giải: Sử dụng một cổng AND cho AB và một cổng OR để kết hợp kết quả với C.
Bài Tập 2: Rút gọn biểu thức logic F = A(B + C) + BC
Rút gọn biểu thức logic F = A(B + C) + BC.
- Lời giải: Sử dụng luật phân phối và luật hấp thụ để rút gọn biểu thức thành F = AB + AC + BC.
Bài Tập 3: Xác định bảng chân lý cho hàm F = (A + B)(C + D)
Xác định bảng chân lý cho hàm F = (A + B)(C + D).
- Lời giải: Tạo bảng chân lý với 4 đầu vào A, B, C, D và tính toán giá trị của F cho tất cả các trường hợp.
Trích dẫn từ chuyên gia Nguyễn Văn A, kỹ sư điện tử kỳ cựu: “Việc thành thạo các bài tập cổng logic cơ bản là bước đầu tiên để thiết kế các hệ thống điện tử số phức tạp.”
Bài Tập 4: Tìm biểu thức logic cho mạch sau… (hình minh họa)
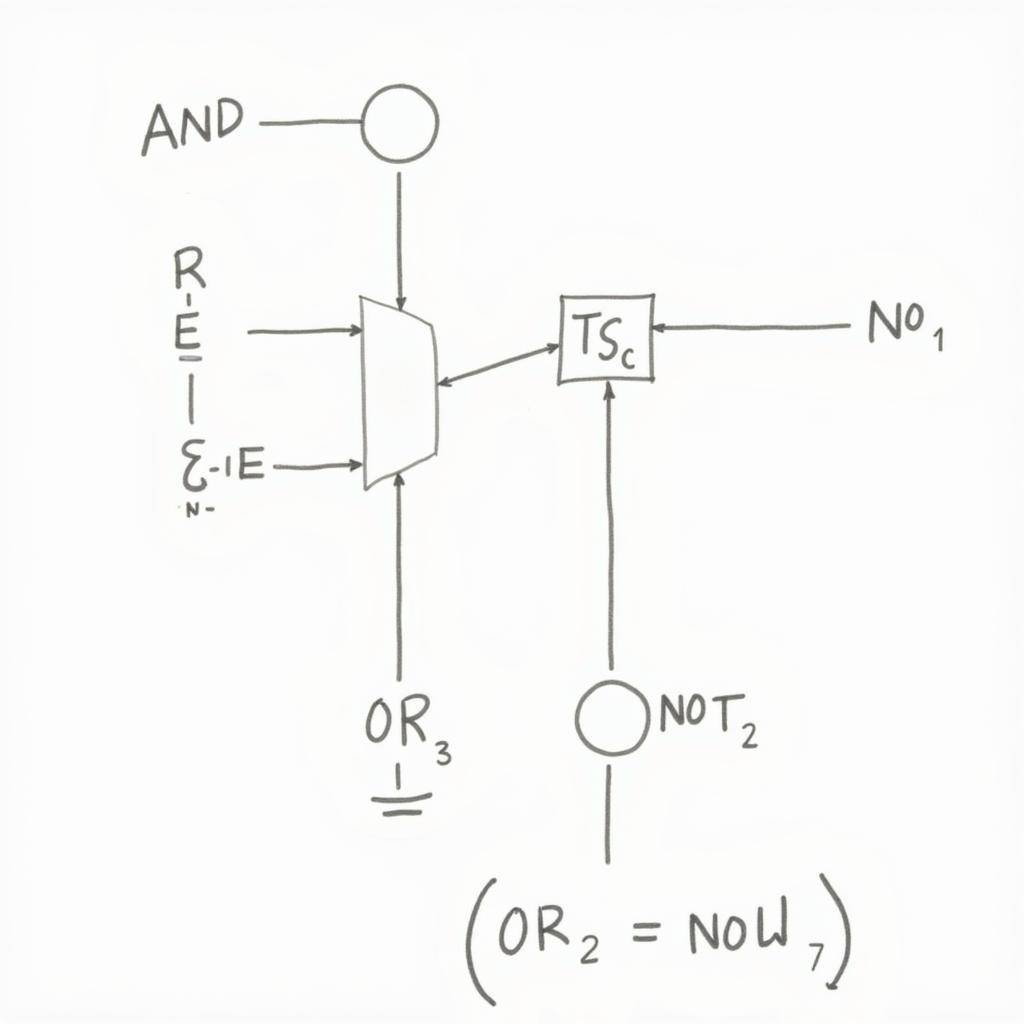Mạch logic bài tập 4
- Lời giải: Phân tích mạch và viết biểu thức logic tương ứng.
Kết luận
Bài tập các cổng logic cơ bản có lời giải giúp người học hiểu rõ hơn về nguyên lý hoạt động của các cổng logic và cách ứng dụng chúng trong thiết kế mạch điện tử. Việc luyện tập thường xuyên với các bài tập này là cần thiết để nắm vững kiến thức cơ bản về điện tử số.
FAQ
- Cổng logic là gì?
- Có bao nhiêu loại cổng logic cơ bản?
- Bảng chân lý là gì?
- Làm sao để rút gọn biểu thức logic?
- Ứng dụng của cổng logic trong thực tế là gì?
- Tại sao cần học về cổng logic?
- Làm sao để phân tích một mạch logic?
Mô tả các tình huống thường gặp câu hỏi.
Người học thường gặp khó khăn trong việc chuyển đổi giữa biểu thức logic và mạch logic, cũng như việc rút gọn biểu thức logic phức tạp.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Xem thêm các bài viết về mạch điện tử số, hệ thống nhúng, và lập trình vi điều khiển.