Bài tập biến đổi Z ngược là một phần quan trọng trong lĩnh vực xử lý tín hiệu số, giúp chuyển đổi miền Z sang miền thời gian. Bài viết này sẽ cung cấp cho bạn kiến thức chuyên sâu về Bài Tập Biến đổi Z Ngược Có Lời Giải, bao gồm các phương pháp giải và ví dụ minh họa. Hãy cùng “Giải Bóng” khám phá thế giới toán học thú vị này.
Bạn đã bao giờ tự hỏi làm thế nào để chuyển đổi một hàm từ miền Z về miền thời gian? Đó chính là lúc biến đổi Z ngược xuất hiện. Việc nắm vững phương pháp biến đổi Z ngược có lời giải rất quan trọng trong việc phân tích và thiết kế hệ thống tín hiệu số. cách giải phê đá
Phương Pháp Giải Bài Tập Biến Đổi Z Ngược
Có nhiều phương pháp để giải bài tập biến đổi Z ngược, mỗi phương pháp đều có ưu điểm và nhược điểm riêng. Dưới đây là một số phương pháp phổ biến:
- Phân tích phân số: Phương pháp này dựa trên việc phân tích hàm Z thành các phân số đơn giản hơn, sau đó tra bảng biến đổi Z để tìm nghiệm tương ứng trong miền thời gian.
- Chia đa thức: Áp dụng khi tử số có bậc lớn hơn hoặc bằng mẫu số.
- Đạo hàm: Phương pháp này sử dụng đạo hàm của biến đổi Z để tìm nghiệm trong miền thời gian.
- Tích chập: Phương pháp này dựa trên tính chất tích chập của biến đổi Z.
Ví Dụ Minh Họa Bài Tập Biến Đổi Z Ngược Có Lời Giải
Để hiểu rõ hơn về các phương pháp giải, chúng ta sẽ cùng xem một số ví dụ minh họa:
Ví dụ 1: Phân tích phân số
Cho hàm Z: X(z) = z / (z-1)(z-2)
Bước 1: Phân tích X(z) thành tổng các phân số đơn giản: X(z) = A/(z-1) + B/(z-2)
Bước 2: Tìm A và B bằng cách giải hệ phương trình.
Bước 3: Tra bảng biến đổi Z để tìm nghiệm tương ứng trong miền thời gian.
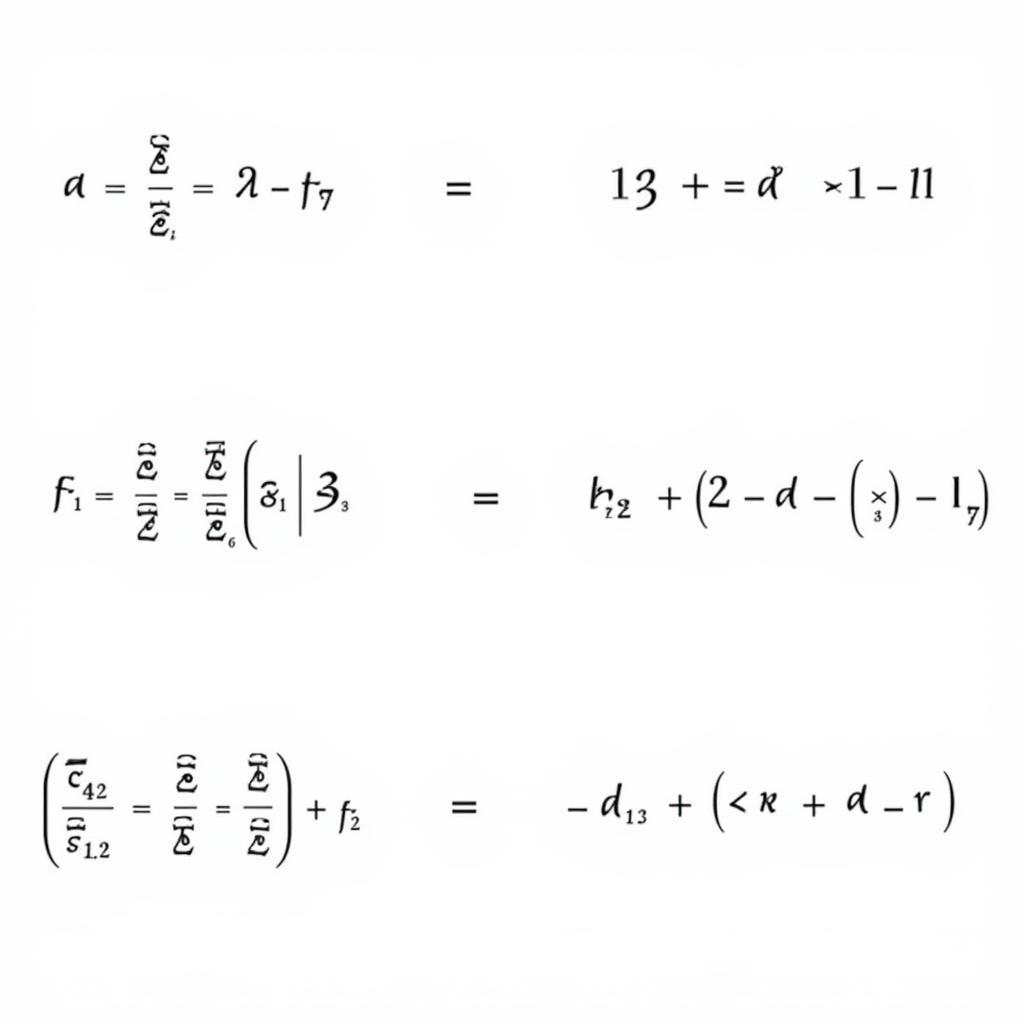Giải bài tập biến đổi Z ngược bằng phương pháp phân tích phân số
Ví dụ 2: Chia đa thức
Cho hàm Z: X(z) = (z^2 + z) / (z-1)
Bước 1: Thực hiện phép chia đa thức (z^2 + z) cho (z-1).
Bước 2: Biểu diễn kết quả dưới dạng tổng các số hạng z^n.
Bước 3: Tra bảng biến đổi Z để tìm nghiệm tương ứng trong miền thời gian.
bài tập mô hình thực erd có lời giải
Ví dụ 3: Đạo hàm
Cho hàm Z: X(z) = z / (z-a)^2
Bước 1: Tìm đạo hàm của biến đổi Z.
Bước 2: Áp dụng công thức biến đổi Z ngược cho đạo hàm.
Kết Luận
Bài tập biến đổi Z ngược có lời giải là một chủ đề quan trọng trong xử lý tín hiệu số. Hiểu rõ các phương pháp giải và áp dụng chúng một cách linh hoạt sẽ giúp bạn giải quyết các bài toán phức tạp trong lĩnh vực này. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về bài tập biến đổi Z ngược.
mối tình đầu của tôi tập 24 vtv giải trí
FAQ
- Biến đổi Z ngược là gì?
- Tại sao cần phải học biến đổi Z ngược?
- Có những phương pháp nào để giải bài tập biến đổi Z ngược?
- Phương pháp nào là tốt nhất để giải bài tập biến đổi Z ngược?
- Làm thế nào để tìm bảng biến đổi Z?
- Ứng dụng của biến đổi Z ngược trong thực tế là gì?
- Tôi có thể tìm thêm bài tập biến đổi Z ngược ở đâu?
Mô tả các tình huống thường gặp câu hỏi.
Người học thường gặp khó khăn trong việc xác định phương pháp phù hợp cho từng bài toán. Việc phân tích cấu trúc của hàm Z là bước quan trọng để lựa chọn phương pháp tối ưu.
Ứng dụng biến đổi Z ngược trong thực tế
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về manh tràng giải phẫu