Giải Bài Tập 4 Trang 55 Giải Tích 12: Hướng Dẫn Chi Tiết Và Bài Tập Tự Luyện

Bài tập 4 trang 55 SGK Giải tích 12 là một trong những bài tập quan trọng trong chương trình Toán lớp 12, giúp học sinh ôn tập và củng cố kiến thức về hàm số, đồ thị và ứng dụng của đạo hàm. Bài viết này sẽ cung cấp cho bạn hướng dẫn giải chi tiết Bài Tập 4 Trang 55 Giải Tích 12, cùng với những bài tập tự luyện bổ sung để bạn nắm vững kiến thức.

Phân Tích Đề Bài Và Hướng Dẫn Giải Chi Tiết Bài Tập 4 Trang 55 Giải Tích 12

Đề bài: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a) y = x³ + 3x² – 4

b) y = -x³ + 3x² – 4

c) y = x⁴ – 2x² + 2

Hướng dẫn giải:

Để giải bài tập này, chúng ta cần thực hiện các bước sau:

Bước 1: Tìm tập xác định

Tất cả các hàm số đã cho đều là hàm đa thức, do đó tập xác định của chúng là R.

Bước 2: Tính đạo hàm y’

a) y’ = 3x² + 6x

b) y’ = -3x² + 6x

c) y’ = 4x³ – 4x

Bước 3: Tìm nghiệm của phương trình y’ = 0 và các điểm đạo hàm không xác định (nếu có)

a) 3x² + 6x = 0 <=> x = 0 hoặc x = -2

b) -3x² + 6x = 0 <=> x = 0 hoặc x = 2

c) 4x³ – 4x = 0 <=> x = 0 hoặc x = 1 hoặc x = -1

Bước 4: Lập bảng biến thiên

Dựa vào dấu của đạo hàm, ta có thể lập bảng biến thiên cho từng hàm số.

Bước 5: Tìm các giới hạn cần thiết

Vì đây là hàm đa thức nên ta chỉ cần tìm giới hạn khi x tiến tới vô cùng.

Bước 6: Vẽ đồ thị

Dựa vào bảng biến thiên và các giới hạn đã tính, ta có thể vẽ đồ thị của từng hàm số.

Hình 1: Đồ thị hàm số y = x³ + 3x² – 4

Hình 2: Đồ thị hàm số y = -x³ + 3x² – 4

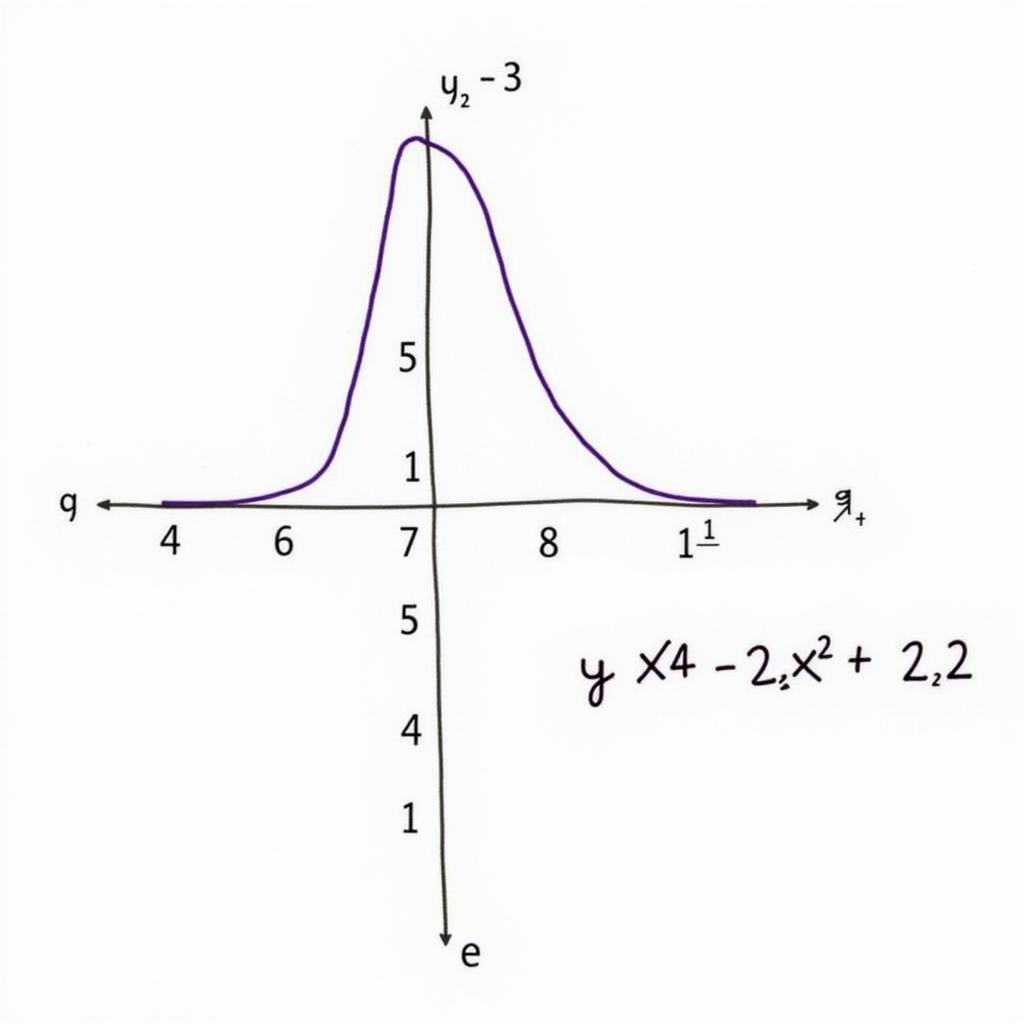Hình 3: Đồ thị hàm số y = x⁴ - 2x² + 2 Hình 3: Đồ thị hàm số y = x⁴ – 2x² + 2

Bài Tập Tự Luyện

Bài 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a) y = x³ – 3x + 2

b) y = -x⁴ + 2x² – 1

c) y = x³ – x² – x + 1

Bài 2: Tìm m để hàm số y = x³ – 3mx² + (m² – 1)x + 2 có hai điểm cực trị.

Bài 3: Tìm m để hàm số y = (m – 1)x⁴ – 2mx² + m + 1 có ba điểm cực trị.

Kết Luận

Bài viết đã cung cấp cho bạn hướng dẫn giải chi tiết bài tập 4 trang 55 Giải tích 12, cùng với những bài tập tự luyện bổ sung. Hy vọng bài viết này sẽ giúp bạn nắm vững kiến thức về khảo sát hàm số và vẽ đồ thị. Hãy thường xuyên luyện tập để nâng cao kỹ năng giải toán của mình.

Câu hỏi thường gặp:

Câu hỏi 1: Tại sao cần phải tìm tập xác định của hàm số trước khi khảo sát sự biến thiên?

Trả lời: Tập xác định của hàm số cho biết giá trị nào của biến số x mà hàm số có nghĩa. Việc xác định tập xác định giúp ta giới hạn phạm vi khảo sát và tránh tính toán cho những giá trị x mà hàm số không xác định.

Câu hỏi 2: Ý nghĩa của việc tìm nghiệm của phương trình y’ = 0 là gì?

Trả lời: Nghiệm của phương trình y’ = 0 chính là hoành độ của các điểm cực trị của hàm số. Tại các điểm này, đồ thị hàm số có thể đạt giá trị lớn nhất, nhỏ nhất cục bộ hoặc là điểm uốn của đồ thị.

Câu hỏi 3: Làm thế nào để xác định được các khoảng đồng biến, nghịch biến của hàm số?

Trả lời: Dựa vào dấu của đạo hàm y’ trên từng khoảng của tập xác định, ta có thể xác định được các khoảng đồng biến, nghịch biến của hàm số. Cụ thể:

Nếu y’ > 0 trên khoảng (a; b) thì hàm số đồng biến trên khoảng (a; b).
Nếu y’ < 0 trên khoảng (a; b) thì hàm số nghịch biến trên khoảng (a; b).

Câu hỏi 4: Ngoài việc sử dụng bảng biến thiên, còn cách nào khác để vẽ đồ thị hàm số?

Trả lời: Bên cạnh việc sử dụng bảng biến thiên, ta có thể vẽ đồ thị hàm số bằng cách:

Lập bảng giá trị: Chọn một số giá trị x thuộc tập xác định, tính giá trị y tương ứng và vẽ các điểm (x; y) lên hệ trục tọa độ. Sau đó, nối các điểm này lại với nhau ta được đồ thị hàm số.
Sử dụng phần mềm vẽ đồ thị: Hiện nay có rất nhiều phần mềm vẽ đồ thị hàm số như Geogebra, Desmos,… giúp ta vẽ đồ thị một cách nhanh chóng và chính xác.

Câu hỏi 5: Có những lưu ý gì khi vẽ đồ thị hàm số?

Trả lời: Khi vẽ đồ thị hàm số, cần lưu ý:

Chọn tỉ lệ x, y trên hệ trục tọa độ phù hợp để đồ thị được hiển thị rõ ràng.
Ghi chú rõ ràng các điểm đặc biệt trên đồ thị như giao điểm với trục hoành, trục tung, các điểm cực trị,…
Vẽ đồ thị bằng nét liền mượt mà, tránh vẽ nét đứt đoạn.

Gợi ý các câu hỏi khác, bài viết khác có trong web:

Liên hệ:

Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.