Bài Giải Phương Trình Lượng Giác 11 Toàn Tập là một chủ đề quan trọng trong chương trình Toán lớp 11. Nắm vững các phương pháp giải phương trình lượng giác sẽ giúp học sinh đạt điểm cao trong các kỳ thi và tạo nền tảng vững chắc cho việc học Toán ở các lớp cao hơn. Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan về các loại phương trình lượng giác thường gặp ở lớp 11 và các phương pháp giải chi tiết, kèm theo ví dụ minh họa.
Bạn đang gặp khó khăn với những bài toán đếm hình lớp 2 có lời giải? Đừng lo, hãy xem ngay hướng dẫn chi tiết tại đây.
Phương Trình Lượng Giác Cơ Bản
Phương trình lượng giác cơ bản là những phương trình có dạng đơn giản, thường được sử dụng làm nền tảng để giải các phương trình phức tạp hơn. Một số dạng phương trình cơ bản bao gồm: sin x = a, cos x = a, tan x = a, cot x = a. Việc giải các phương trình này chủ yếu dựa vào việc sử dụng vòng tròn lượng giác và các công thức lượng giác cơ bản.
Giải Phương Trình sin x = a
Để giải phương trình sin x = a, ta cần xác định giá trị của a. Nếu |a| > 1, phương trình vô nghiệm. Nếu |a| ≤ 1, phương trình có nghiệm. Ví dụ: sin x = 1/2. Nghiệm của phương trình là x = π/6 + k2π và x = 5π/6 + k2π (k ∈ Z).
Giải Phương Trình cos x = a
Tương tự như phương trình sin x = a, để giải phương trình cos x = a, ta cũng cần xác định giá trị của a. Ví dụ: cos x = -√3/2. Nghiệm của phương trình là x = ±5π/6 + k2π (k ∈ Z).
 Giải Phương Trình Lượng Giác Cơ Bản
Giải Phương Trình Lượng Giác Cơ Bản
Giải Phương Trình tan x = a và cot x = a
Phương trình tan x = a và cot x = a luôn có nghiệm với mọi giá trị của a. Ví dụ: tan x = 1. Nghiệm của phương trình là x = π/4 + kπ (k ∈ Z).
Phương Trình Lượng Giác Thường Gặp
Ngoài các phương trình lượng giác cơ bản, học sinh lớp 11 còn gặp một số dạng phương trình phức tạp hơn, đòi hỏi phải sử dụng các công thức biến đổi lượng giác.
Phương Trình Bậc Hai Đối Với Một Hàm Lượng Giác
Dạng phương trình này có thể được giải bằng cách đặt ẩn phụ. Ví dụ: 2sin²x – sin x – 1 = 0. Đặt t = sin x, ta được phương trình bậc hai 2t² – t – 1 = 0.
Bài tập trắc địa có lời giải là một tài liệu hữu ích cho các bạn học chuyên ngành trắc địa.
Phương Trình Dạng asin x + bcos x = c
Để giải phương trình này, ta có thể sử dụng phương pháp chia cả hai vế cho √(a² + b²). Ví dụ: sin x + √3cos x = 2.
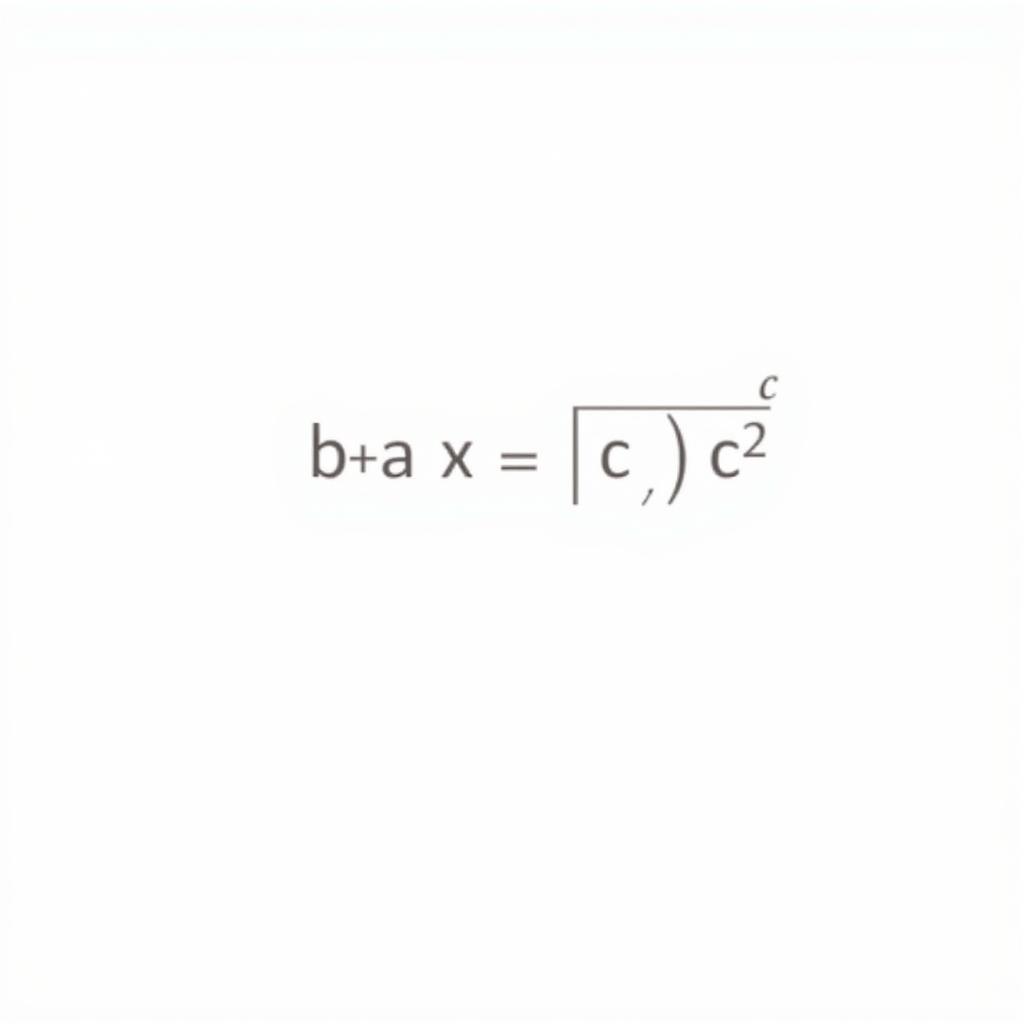 Giải Phương Trình Lượng Giác Dạng asinx + bcosx = c
Giải Phương Trình Lượng Giác Dạng asinx + bcosx = c
Phương Trình Hàm Lượng Giác Bậc Cao
Đối với phương trình hàm lượng giác bậc cao, ta cần sử dụng các công thức biến đổi lượng giác để hạ bậc.
Bạn muốn giải toán hình lớp 6 một cách dễ dàng? Hãy tham khảo bài viết này để biết thêm chi tiết.
Kết Luận
Bài giải phương trình lượng giác 11 toàn tập đòi hỏi học sinh phải nắm vững các công thức lượng giác và các phương pháp giải. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết để giải quyết các bài toán liên quan đến phương trình lượng giác lớp 11.
 Phương Trình Lượng Giác Bậc Cao
Phương Trình Lượng Giác Bậc Cao
FAQ
- Phương trình lượng giác là gì?
- Làm thế nào để giải phương trình sin x = a?
- Cách giải phương trình cos x = a như thế nào?
- Phương pháp giải phương trình tan x = a và cot x = a?
- Làm sao để giải phương trình lượng giác dạng asin x + bcos x = c?
- Phương trình lượng giác bậc hai đối với một hàm lượng giác được giải như thế nào?
- Cách giải phương trình hàm lượng giác bậc cao?
Tìm hiểu thêm về bài tập đại số và giải tích nâng cao 11.
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn khi biến đổi phương trình lượng giác về dạng cơ bản. Việc áp dụng sai công thức hoặc biến đổi sai dấu là những lỗi thường gặp. Ngoài ra, việc xác định đúng điều kiện của nghiệm cũng là một vấn đề cần lưu ý.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về giải phiếu bài tập toán lớp 5 trên website của chúng tôi.
