Trong hình học phẳng, đường trung trực của một đoạn thẳng giữ một vai trò quan trọng trong việc xác định vị trí các điểm có khoảng cách bằng nhau đến hai đầu mút của đoạn thẳng đó. Việc hiểu rõ Bài Giải Chứng Minh đường Trung Trực Của đoạn Thẳng không chỉ giúp học sinh nắm vững kiến thức hình học cơ bản mà còn tạo nền tảng vững chắc cho việc học tập các kiến thức nâng cao hơn.
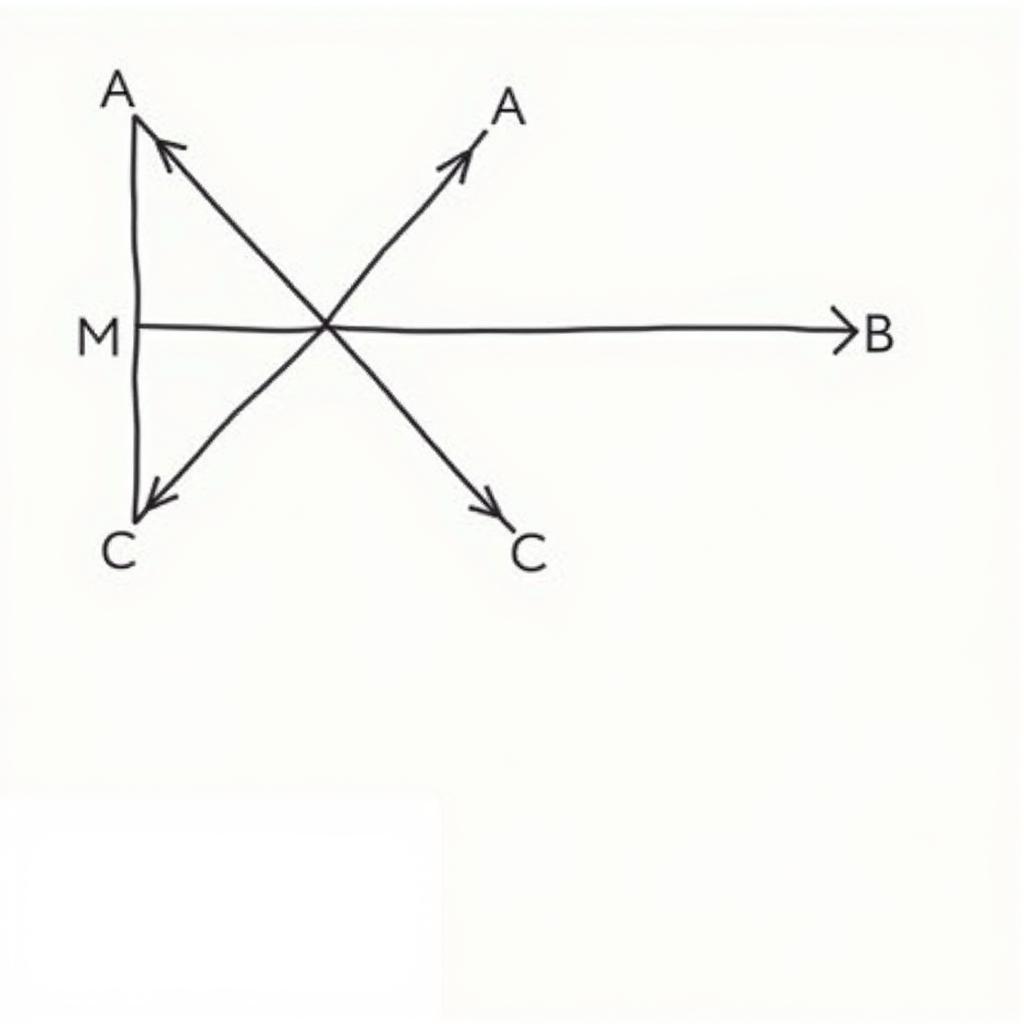 Đường trung trực của đoạn thẳng AB
Đường trung trực của đoạn thẳng AB
Định Nghĩa Đường Trung Trực
Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của nó.
Ví dụ, cho đoạn thẳng AB. Đường thẳng d được gọi là đường trung trực của đoạn thẳng AB nếu d vuông góc với AB tại trung điểm M của AB.
Tính Chất Của Đường Trung Trực
Tính chất 1: Mọi điểm nằm trên đường trung trực của một đoạn thẳng đều cách đều hai đầu mút của đoạn thẳng đó.
Chứng minh:
Cho đoạn thẳng AB, đường trung trực d cắt AB tại trung điểm M. Lấy điểm C bất kỳ trên d.
Xét tam giác AMC và tam giác BMC, ta có:
- AM = BM (M là trung điểm AB)
- góc AMC = góc BMC = 90 độ (d vuông góc AB)
- Cạnh MC chung
Suy ra tam giác AMC bằng tam giác BMC (cạnh – góc – cạnh)
=> AC = BC (hai cạnh tương ứng)
Vậy điểm C nằm trên đường trung trực d của đoạn thẳng AB cách đều hai đầu mút A và B.
Tính chất 2: Mọi điểm cách đều hai đầu mút của một đoạn thẳng đều nằm trên đường trung trực của đoạn thẳng đó.
Chứng minh:
Cho đoạn thẳng AB. Lấy điểm D sao cho DA = DB. Gọi M là trung điểm của AB.
Xét tam giác DAM và tam giác DBM, ta có:
- DA = DB (giả thiết)
- AM = BM (M là trung điểm AB)
- Cạnh DM chung
Suy ra tam giác DAM bằng tam giác DBM (cạnh – cạnh – cạnh)
=> góc DMA = góc DMB (hai góc tương ứng)
Mà góc DMA + góc DMB = 180 độ (hai góc kề bù)
=> góc DMA = góc DMB = 90 độ
=> DM vuông góc AB tại M
Vậy điểm D cách đều hai đầu mút A và B của đoạn thẳng AB nằm trên đường trung trực của AB.
Ý Nghĩa Của Đường Trung Trực
Đường trung trực của đoạn thẳng có ý nghĩa quan trọng trong hình học và ứng dụng thực tiễn:
- Xác định tâm đường tròn ngoại tiếp tam giác: Đường trung trực của mỗi cạnh tam giác sẽ cắt nhau tại một điểm, điểm đó chính là tâm đường tròn ngoại tiếp tam giác.
- Ứng dụng trong xây dựng: Trong thực tế, người ta sử dụng tính chất của đường trung trực để xác định vị trí đặt cột điện, cột đèn sao cho cách đều các vị trí cần chiếu sáng.
Bài Tập Vận Dụng
-
Cho tam giác ABC có AB = 5cm, AC = 7cm. Gọi M là trung điểm của BC. Qua M, kẻ đường thẳng vuông góc với BC cắt AB tại D. Chứng minh D là trung điểm của AB.
-
Cho hai điểm A, B cố định. Tìm tập hợp các điểm M sao cho MA = MB.
Kết Luận
Bài giải chứng minh đường trung trực của đoạn thẳng cung cấp cho chúng ta kiến thức nền tảng về một khái niệm quan trọng trong hình học phẳng. Nắm vững định nghĩa, tính chất và ý nghĩa của đường trung trực sẽ giúp ích rất nhiều cho việc học tập và giải quyết các bài toán hình học phức tạp hơn.
FAQs
1. Đường trung trực của đoạn thẳng có cắt đoạn thẳng đó không?
Có, đường trung trực của đoạn thẳng luôn cắt đoạn thẳng đó tại trung điểm.
2. Có bao nhiêu đường trung trực đi qua một đoạn thẳng?
Chỉ có duy nhất một đường trung trực đi qua một đoạn thẳng.
3. Làm thế nào để vẽ đường trung trực của một đoạn thẳng bằng thước và compa?
Bạn có thể tham khảo các video hướng dẫn trên internet hoặc sách giáo khoa hình học lớp 7.
4. Đường trung trực có liên quan gì đến đường tròn không?
Có, tâm của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh tam giác.
5. Ngoài ứng dụng trong xây dựng, đường trung trực còn được ứng dụng trong lĩnh vực nào khác?
Đường trung trực còn được ứng dụng trong nhiều lĩnh vực khác như thiết kế, đồ họa, viễn thông,…
Bạn cần hỗ trợ?
Liên hệ ngay với chúng tôi!
Số Điện Thoại: 02033846993
Email: [email protected]
Địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam.
Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
