Trong bóng đá, chiến thuật di chuyển của các cầu thủ đôi khi giống như những đường thẳng song song, không bao giờ giao nhau nhưng lại hỗ trợ và bổ sung cho nhau. Việc tìm hiểu về “Bài Giải Chứng Minh 2 đường Thẳng Song Song” cũng tương tự như phân tích chiến thuật bóng đá, đòi hỏi sự quan sát tỉ mỉ và tư duy logic. Bài viết này sẽ đi sâu vào cách chứng minh hai đường thẳng song song, từ những kiến thức cơ bản đến các ứng dụng phức tạp hơn. Bạn sẽ tìm thấy những phương pháp chứng minh, ví dụ minh họa và những câu hỏi thường gặp giúp bạn nắm vững kiến thức này. Nếu bạn quan tâm đến Giải thoát đam mỹ, hãy xem thêm tại đây: giải thoát đam mỹ.
Các Phương Pháp Chứng Minh Hai Đường Thẳng Song Song
Có nhiều cách để chứng minh hai đường thẳng song song. Dưới đây là một số phương pháp phổ biến:
- Sử dụng góc đồng vị: Nếu hai đường thẳng bị cắt bởi một đường thẳng thứ ba tạo thành các cặp góc đồng vị bằng nhau, thì hai đường thẳng đó song song.
- Sử dụng góc so le trong: Nếu hai đường thẳng bị cắt bởi một đường thẳng thứ ba tạo thành các cặp góc so le trong bằng nhau, thì hai đường thẳng đó song song.
- Sử dụng góc trong cùng phía: Nếu hai đường thẳng bị cắt bởi một đường thẳng thứ ba tạo thành các cặp góc trong cùng phía bù nhau, thì hai đường thẳng đó song song.
- Sử dụng tính chất của đường trung bình: Đường thẳng đi qua trung điểm của một cạnh của tam giác và song song với cạnh thứ hai thì bằng một nửa cạnh thứ ba và cắt cạnh thứ ba tại trung điểm của nó.
Bài Giải Chứng Minh 2 Đường Thẳng Song Song: Ví Dụ Minh Họa
Để hiểu rõ hơn về cách áp dụng các phương pháp trên, chúng ta hãy cùng xem xét một vài ví dụ.
Ví dụ 1: Chứng minh hai đường thẳng song song bằng góc đồng vị
Cho hai đường thẳng a và b bị cắt bởi đường thẳng c. Biết góc A1 = góc B1 (là hai góc đồng vị). Chứng minh a // b.
Vì góc A1 = góc B1 (giả thiết) mà đây là hai góc đồng vị nên a // b.
Ví dụ 2: Chứng minh hai đường thẳng song song bằng góc so le trong
Cho hai đường thẳng a và b bị cắt bởi đường thẳng c. Biết góc A2 = góc B1 (là hai góc so le trong). Chứng minh a // b.
Vì góc A2 = góc B1 (giả thiết) mà đây là hai góc so le trong nên a // b.
Bạn có thể xem thêm về cấu trúc giải phẫu bụng tại caasu trúc giải phẫu bụng.
Bài Giải Chứng Minh 2 Đường Thẳng Song Song: Ứng Dụng Trong Hình Học
Việc chứng minh hai đường thẳng song song có rất nhiều ứng dụng trong hình học, đặc biệt là trong việc chứng minh các định lý và tính toán các đại lượng hình học.
“Chứng minh hai đường thẳng song song là một kỹ năng cơ bản nhưng quan trọng trong hình học. Nó giúp chúng ta hiểu sâu hơn về mối quan hệ giữa các đường thẳng và các góc.” – Nguyễn Văn A, Giáo sư Toán học.
Ví dụ 3: Chứng minh hình bình hành
Cho tứ giác ABCD có AB // CD và AD // BC. Chứng minh ABCD là hình bình hành.
Vì AB // CD và AD // BC (giả thiết) nên ABCD là hình bình hành (theo định nghĩa hình bình hành).
“Việc nắm vững các phương pháp chứng minh hai đường thẳng song song sẽ giúp học sinh giải quyết nhiều bài toán hình học phức tạp hơn.” – Trần Thị B, Giáo viên Toán.
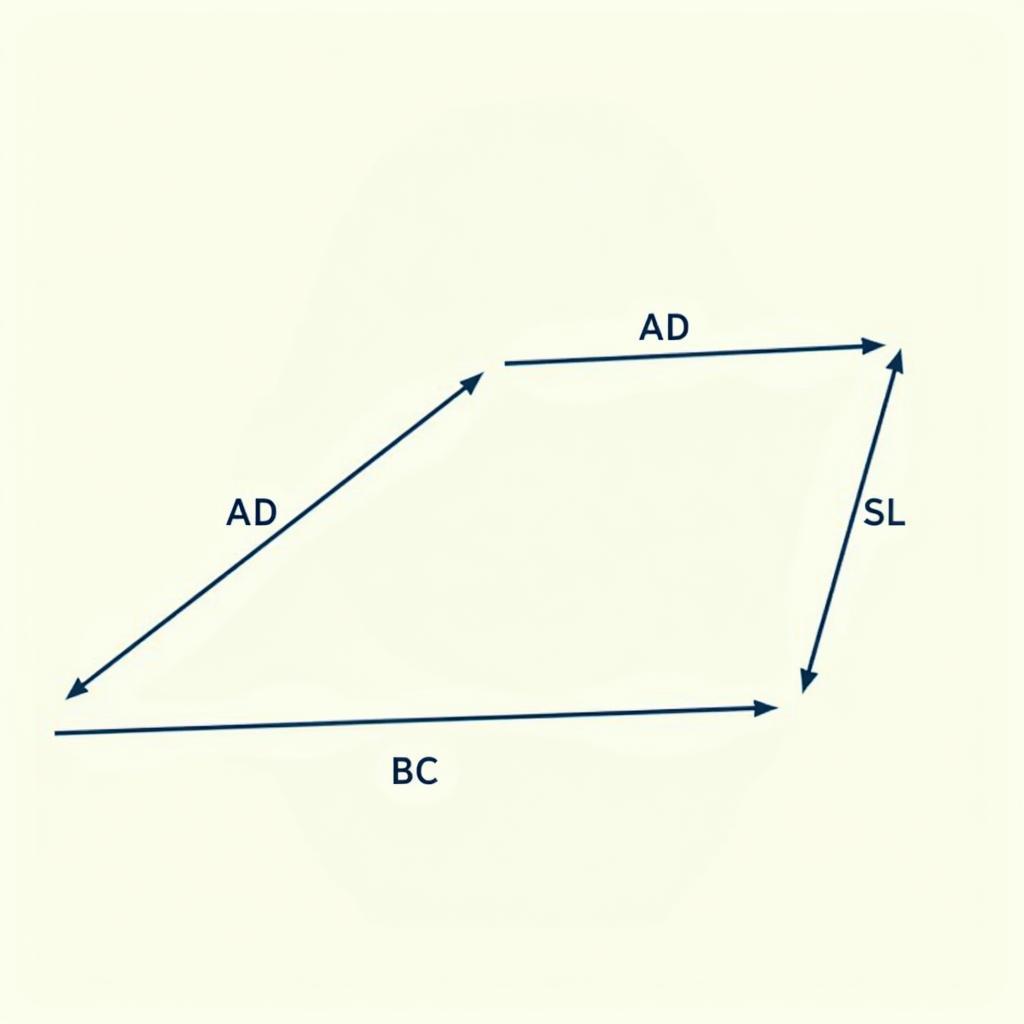 Minh họa chứng minh hình bình hành
Minh họa chứng minh hình bình hành
Xem thêm về trực tiếp giải tây ban nha tại trực tiếp giải tây ban nha.
Kết luận
Bài giải chứng minh 2 đường thẳng song song là một phần quan trọng trong hình học. Hiểu rõ các phương pháp chứng minh và biết cách áp dụng chúng sẽ giúp bạn giải quyết nhiều bài toán hình học khác nhau. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về bài giải chứng minh 2 đường thẳng song song.
Mô tả các tình huống thường gặp câu hỏi
Khi làm bài tập về chứng minh hai đường thẳng song song, học sinh thường gặp khó khăn trong việc xác định các cặp góc đồng vị, so le trong, trong cùng phía.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về Bè nhãn giải phẫu mắt tại bè nhãn giải phẫu mắt và BTS nhận giải 2017 tại bts nhận giải 2017.
Kêu gọi hành động:
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
