Phương trình đường elip là một chủ đề quan trọng trong hình học giải tích lớp 10. Bài viết này sẽ hướng dẫn bạn giải các bài tập liên quan đến bài 3 phương trình đường elip, từ cơ bản đến nâng cao. Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất và các dạng bài tập thường gặp, giúp bạn nắm vững kiến thức và tự tin chinh phục mọi bài toán elip.
Phương Trình Đường Elip là gì?
Phương trình đường elip có dạng chuẩn là $frac{x^2}{a^2} + frac{y^2}{b^2} = 1$ (với $a > b > 0$). Elip là một đường cong kín, có hai trục đối xứng và tâm đối xứng. Hiểu rõ phương trình này là chìa khóa để giải các bài tập liên quan. Các đại lượng $a$ và $b$ lần lượt là độ dài bán trục lớn và bán trục nhỏ của elip.
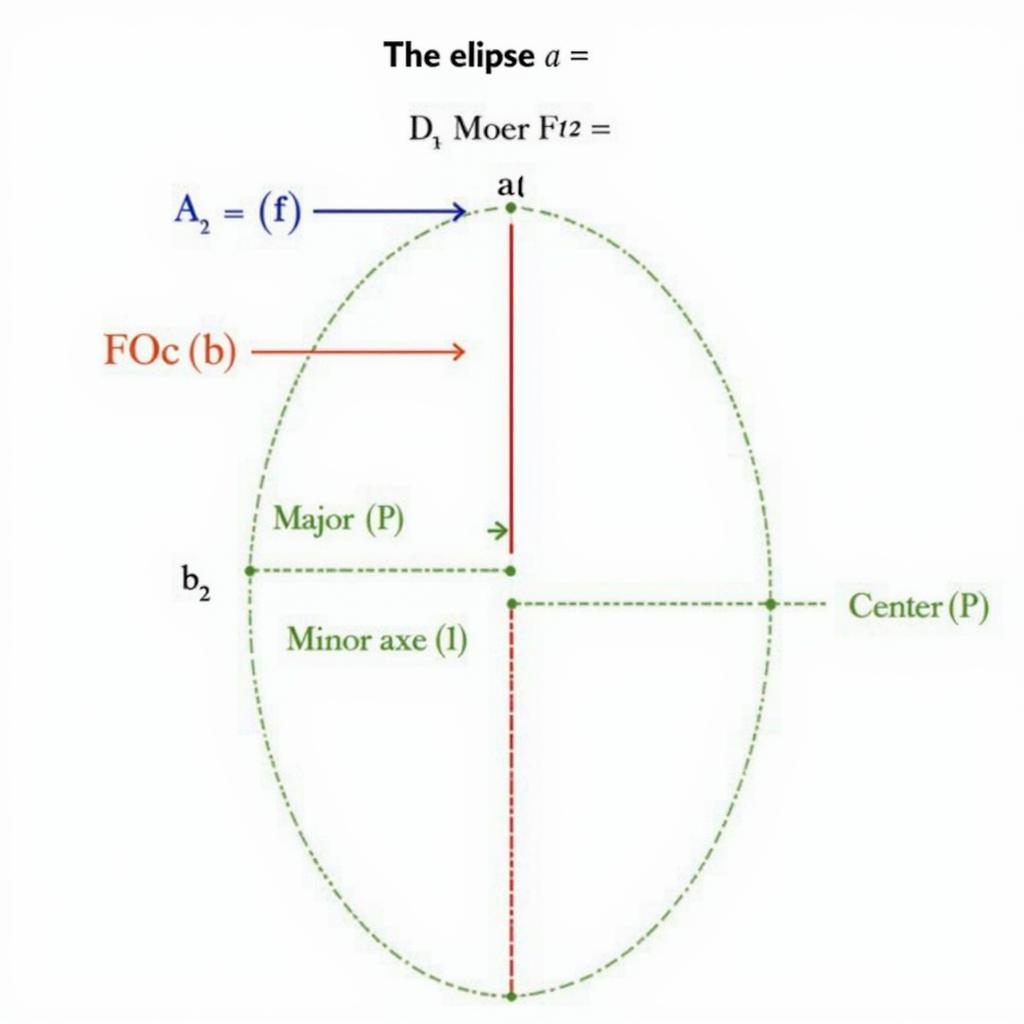 Phương trình đường elip và các thành phần
Phương trình đường elip và các thành phần
Xác Định Phương Trình Elip
Để xác định phương trình elip, ta cần biết các thông số như độ dài bán trục lớn ($a$), bán trục nhỏ ($b$), tọa độ tiêu điểm, hoặc các thông tin khác về hình dạng và vị trí của elip. Thông qua các bài tập cụ thể, chúng ta sẽ tìm hiểu cách áp dụng công thức và phương pháp để tìm ra phương trình elip. bài tập elip 10 có lời giải cung cấp nhiều ví dụ minh họa chi tiết.
Cách Tìm Phương Trình Elip Qua Tiêu Điểm
Nếu biết tọa độ tiêu điểm và độ dài trục lớn, ta có thể dễ dàng tìm ra phương trình elip. Ví dụ, nếu tiêu điểm nằm trên trục hoành, ta có $c^2 = a^2 – b^2$, từ đó tính được $b$ và viết được phương trình elip.
 Tìm phương trình elip qua tiêu điểm
Tìm phương trình elip qua tiêu điểm
Ví Dụ Giải Bài Tập Elip
Giả sử một elip có tiêu điểm $F_1(-4, 0)$, $F_2(4, 0)$ và độ dài trục lớn bằng 10. Ta có $2c = 8$ nên $c = 4$ và $2a = 10$ nên $a = 5$. Từ $c^2 = a^2 – b^2$, ta có $b^2 = a^2 – c^2 = 25 – 16 = 9$. Vậy phương trình elip là $frac{x^2}{25} + frac{y^2}{9} = 1$. Bạn có thể tìm thêm bài tập về parabol lớp 10 có lời giải để luyện tập thêm về các đường conic khác.
Bài Toán Elip Nâng Cao
Các bài toán elip nâng cao thường yêu cầu vận dụng linh hoạt các kiến thức về phương trình elip, kết hợp với các kiến thức hình học khác. giải toán bằng cách lập phương trình lop 9 có thể giúp bạn rèn luyện kỹ năng lập phương trình.
Ứng Dụng Của Elip Trong Thực Tế
Elip có nhiều ứng dụng trong thực tế, ví dụ như trong thiết kế quỹ đạo vệ tinh, xây dựng cầu, và kiến trúc. Hiểu rõ bài 3 phương trình đường elip giúp chúng ta áp dụng kiến thức vào các lĩnh vực này.
 Ứng dụng của elip trong thực tế
Ứng dụng của elip trong thực tế
Kết luận
Bài 3 phương trình đường elip là nền tảng quan trọng trong hình học giải tích. Nắm vững kiến thức về phương trình elip, cách xác định phương trình và giải các bài tập liên quan sẽ giúp bạn thành công trong học tập. bài tập elip lớp 10 có lời giải trắc nghiệm sẽ giúp bạn củng cố kiến thức. viết chương trình giải phương trình bậc 2 trong c có thể hữu ích nếu bạn muốn tìm hiểu về giải phương trình bằng lập trình.
FAQ
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: giaibongda@gmail.com Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
