Bài tập số 2 trang 84 SGK Giải Tích 12 là một bài tập kinh điển, giúp học sinh lớp 12 ôn tập và củng cố kiến thức về hàm số lũy thừa. Bài tập yêu cầu học sinh tìm tập xác định, đạo hàm, và khảo sát sự biến thiên của các hàm số lũy thừa với số mũ hữu tỉ. Thông qua việc giải bài tập này, học sinh sẽ nắm vững được các tính chất quan trọng của hàm số lũy thừa, từ đó áp dụng vào giải quyết các bài toán phức tạp hơn.
Tập Xác Định của Hàm Số Lũy Thừa: Nơi Hàm Số “Tồn Tại”
Tập xác định của một hàm số là tập hợp tất cả các giá trị mà biến số có thể nhận được để hàm số đó xác định. Đối với hàm số lũy thừa, việc xác định tập xác định phụ thuộc vào số mũ của nó:
- Số mũ nguyên dương: Hàm số xác định trên toàn bộ tập số thực (R).
- Số mũ nguyên âm: Hàm số xác định trên tập số thực trừ đi giá trị làm cho mẫu số bằng 0.
- Số mũ hữu tỉ: Hàm số xác định khi và chỉ khi cơ số lớn hơn 0.
Đạo Hàm của Hàm Số Lũy Thừa: “Tốc Độ Thay Đổi” của Hàm Số
Đạo hàm của một hàm số cho biết tốc độ thay đổi của hàm số đó tại một điểm. Đối với hàm số lũy thừa y = x^n, đạo hàm của nó được tính theo công thức:
y’ = n*x^(n-1)
Công thức này có thể áp dụng cho cả ba trường hợp số mũ nguyên dương, nguyên âm và hữu tỉ.
Khảo Sát Sự Biến Thiên: “Bản Đồ” của Hàm Số
Khảo sát sự biến thiên của một hàm số là việc tìm hiểu cách hàm số đó thay đổi (tăng, giảm) trên tập xác định của nó. Để khảo sát sự biến thiên của hàm số lũy thừa, ta cần thực hiện các bước sau:
- Tìm tập xác định: Xác định tập hợp các giá trị mà biến số có thể nhận.
- Tính đạo hàm: Tính đạo hàm của hàm số để xác định khoảng đồng biến và nghịch biến.
- Lập bảng biến thiên: Tóm tắt các thông tin về sự biến thiên của hàm số.
- Vẽ đồ thị: Minh họa hình ảnh của hàm số dựa trên bảng biến thiên.
Bài 2 Trang 84 SGK Giải Tích 12: Vận Dụng Kiến Thức
Bài tập số 2 trang 84 SGK Giải Tích 12 yêu cầu học sinh vận dụng các kiến thức đã học về hàm số lũy thừa để tìm tập xác định, đạo hàm và khảo sát sự biến thiên của một số hàm số cụ thể.
Ví Dụ Minh Họa:
Cho hàm số y = x^(2/3). Hãy tìm tập xác định, đạo hàm và khảo sát sự biến thiên của hàm số.
Lời giải:
-
Tập xác định: Vì số mũ là hữu tỉ (2/3), nên hàm số xác định khi x > 0. Vậy tập xác định của hàm số là D = (0; +∞).
-
Đạo hàm: Áp dụng công thức tính đạo hàm, ta có:
y’ = (2/3)x^((2/3)-1) = (2/3)x^(-1/3) -
Khảo sát sự biến thiên:
-
Hàm số đồng biến trên khoảng (0; +∞) vì y’ > 0 với mọi x thuộc (0; +∞).
-
Hàm số không có cực trị.
-
-
Đồ thị: Dựa vào bảng biến thiên, ta có thể vẽ đồ thị của hàm số.
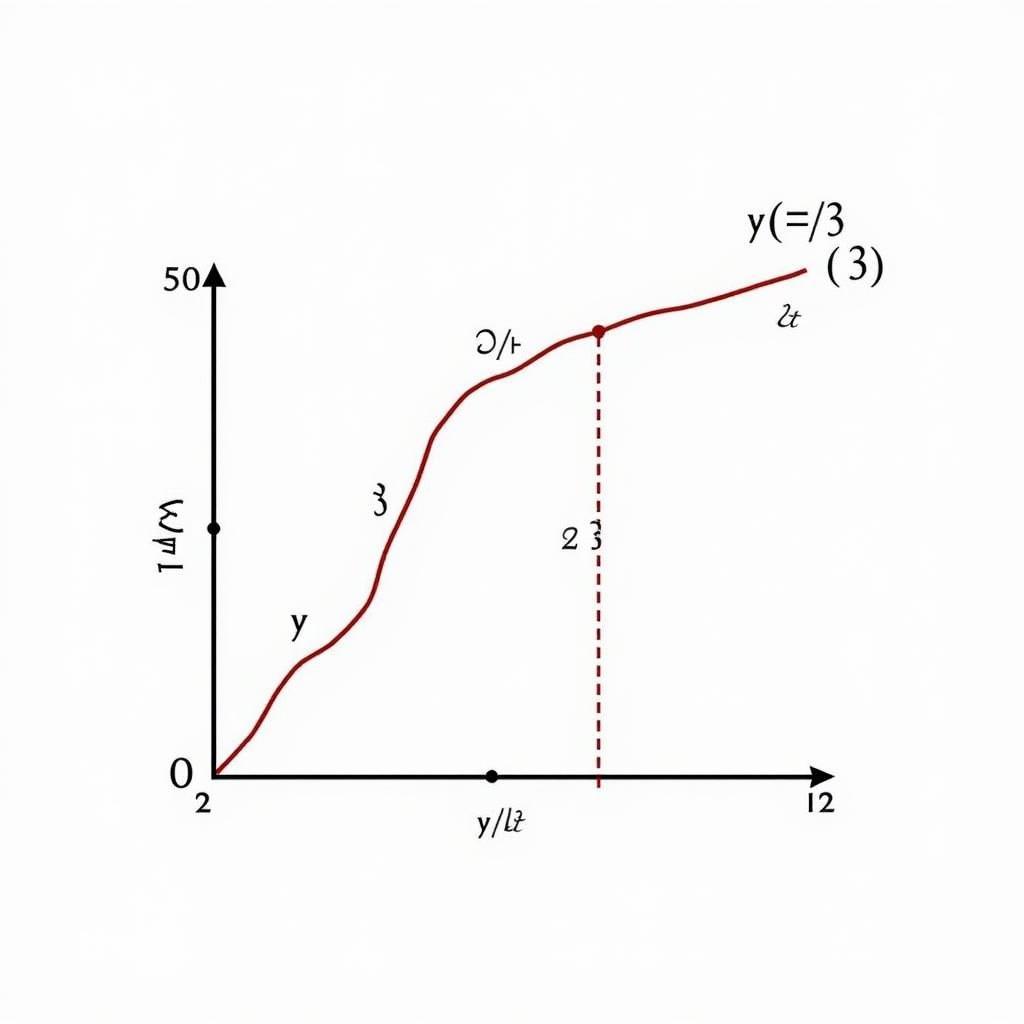Đồ thị hàm số lũy thừa
Kết Luận: Nắm Vững Kiến Thức, Vận Dụng Thành Thạo
Bài 2 Trang 84 Sgk Giải Tích 12 là một bài tập quan trọng, giúp học sinh củng cố kiến thức về hàm số lũy thừa. Bằng cách nắm vững các khái niệm cơ bản và luyện tập thường xuyên, học sinh sẽ tự tin giải quyết các bài toán liên quan đến hàm số lũy thừa một cách hiệu quả.
Bạn muốn tìm hiểu thêm về các dạng bài tập khác của hàm số lũy thừa? Hãy tham khảo các bài viết liên quan trên Giải Bóng:
Cần hỗ trợ thêm về bài 2 trang 84 sgk giải tích 12 hoặc các vấn đề toán học khác?
Liên hệ ngay:
- Số Điện Thoại: 02033846993
- Email: [email protected]
- Địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam.
Đội ngũ Giải Bóng luôn sẵn sàng hỗ trợ bạn 24/7!