Chương 1 của chương trình Toán hình học lớp 9 là nền tảng quan trọng, trang bị cho học sinh những kiến thức cơ bản về hình học phẳng, đặc biệt là tam giác và đường tròn. Nắm vững nội dung chương này sẽ giúp các em tự tin hơn khi tiếp cận các kiến thức nâng cao ở các chương tiếp theo.
Ôn Tập Các Kiến Thức Trọng Tâm Giải Toán 9 Hình Học Chương 1
1. Tam Giác
1.1. Định Nghĩa và Phân Loại Tam Giác
- Định nghĩa: Tam giác là hình gồm ba đoạn thẳng được tạo thành từ ba điểm không thẳng hàng.
- Phân loại:
- Tam giác cân: là tam giác có hai cạnh bằng nhau.
- Tam giác đều: là tam giác có ba cạnh bằng nhau.
- Tam giác vuông: là tam giác có một góc vuông.
- Tam giác vuông cân: là tam giác vuông có hai cạnh góc vuông bằng nhau.
Các loại tam giác
1.2. Các Đường Đặc Biệt Trong Tam Giác
- Đường trung tuyến: là đoạn thẳng nối từ đỉnh của tam giác đến trung điểm cạnh đối diện.
- Đường cao: là đoạn thẳng vẽ từ một đỉnh của tam giác và vuông góc với cạnh đối diện.
- Đường trung trực: là đường thẳng vuông góc với một cạnh của tam giác tại trung điểm của cạnh đó.
- Đường phân giác: là đường thẳng chia một góc của tam giác thành hai góc bằng nhau.
Lưu ý:
- Ba đường trung tuyến của tam giác đồng quy tại một điểm, điểm đó được gọi là trọng tâm của tam giác.
- Ba đường cao của tam giác đồng quy tại một điểm, điểm đó được gọi là trực tâm của tam giác.
- Ba đường trung trực của tam giác đồng quy tại một điểm, điểm đó là tâm đường tròn ngoại tiếp của tam giác.
- Ba đường phân giác của tam giác đồng quy tại một điểm, điểm đó là tâm đường tròn nội tiếp của tam giác.
1.3. Các Hệ Thức Lượng Trong Tam Giác Vuông
- Định lý Pytago: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
- Hệ thức giữa cạnh và góc trong tam giác vuông:
sin α = đối / huyềncos α = kề / huyềntan α = đối / kềcot α = kề / đối
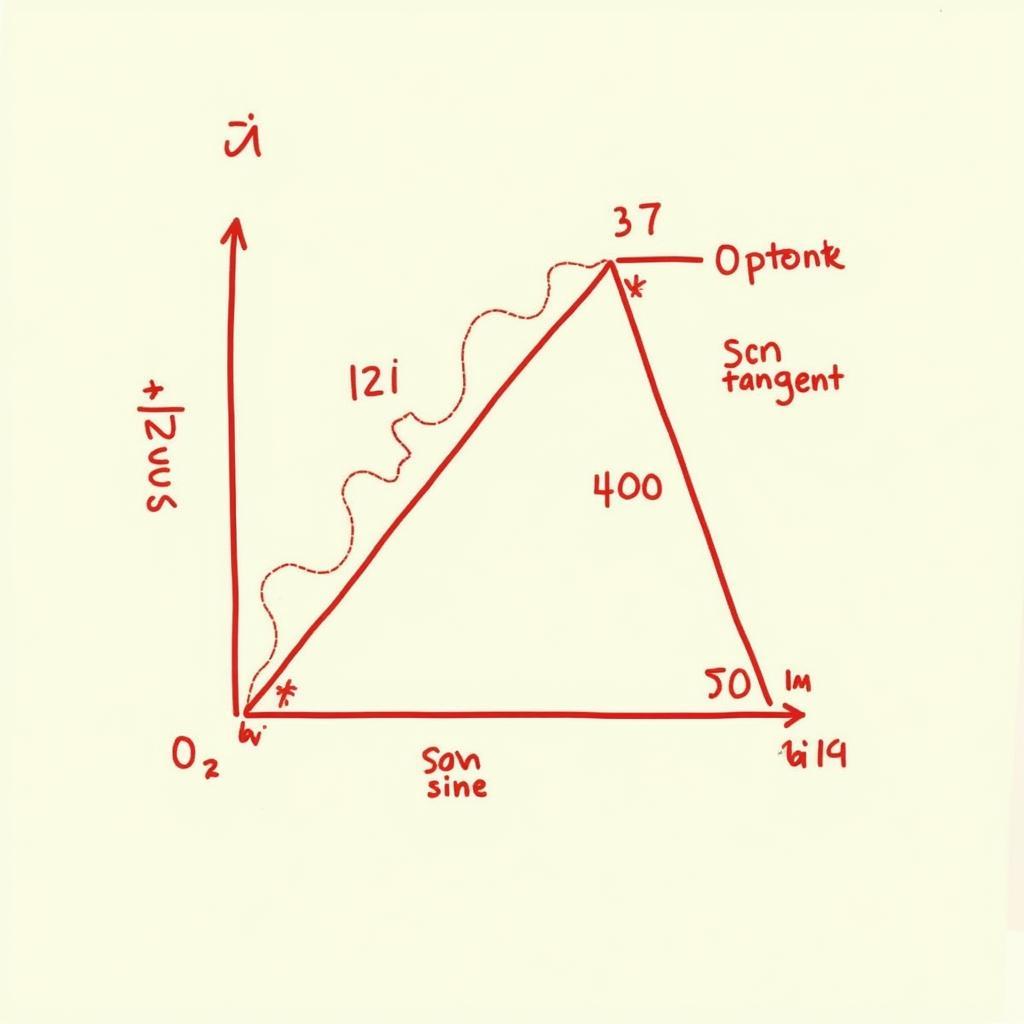Hệ thức lượng trong tam giác vuông
2. Đường Tròn
2.1. Định Nghĩa và Các Yếu Tố Liên Quan
- Đường tròn: là tập hợp tất cả các điểm trên mặt phẳng cách đều một điểm cho trước một khoảng cách không đổi. Điểm cho trước gọi là tâm, khoảng cách không đổi gọi là bán kính.
- Đường kính: là đoạn thẳng đi qua tâm và nối hai điểm trên đường tròn.
- Cung: là một phần của đường tròn nằm giữa hai điểm trên đường tròn.
- Dây cung: là đoạn thẳng nối hai điểm trên đường tròn.
2.2. Vị Trí Tương Đối Giữa Điểm Và Đường Tròn
- Điểm nằm trong đường tròn: Khoảng cách từ điểm đến tâm nhỏ hơn bán kính.
- Điểm nằm trên đường tròn: Khoảng cách từ điểm đến tâm bằng bán kính.
- Điểm nằm ngoài đường tròn: Khoảng cách từ điểm đến tâm lớn hơn bán kính.
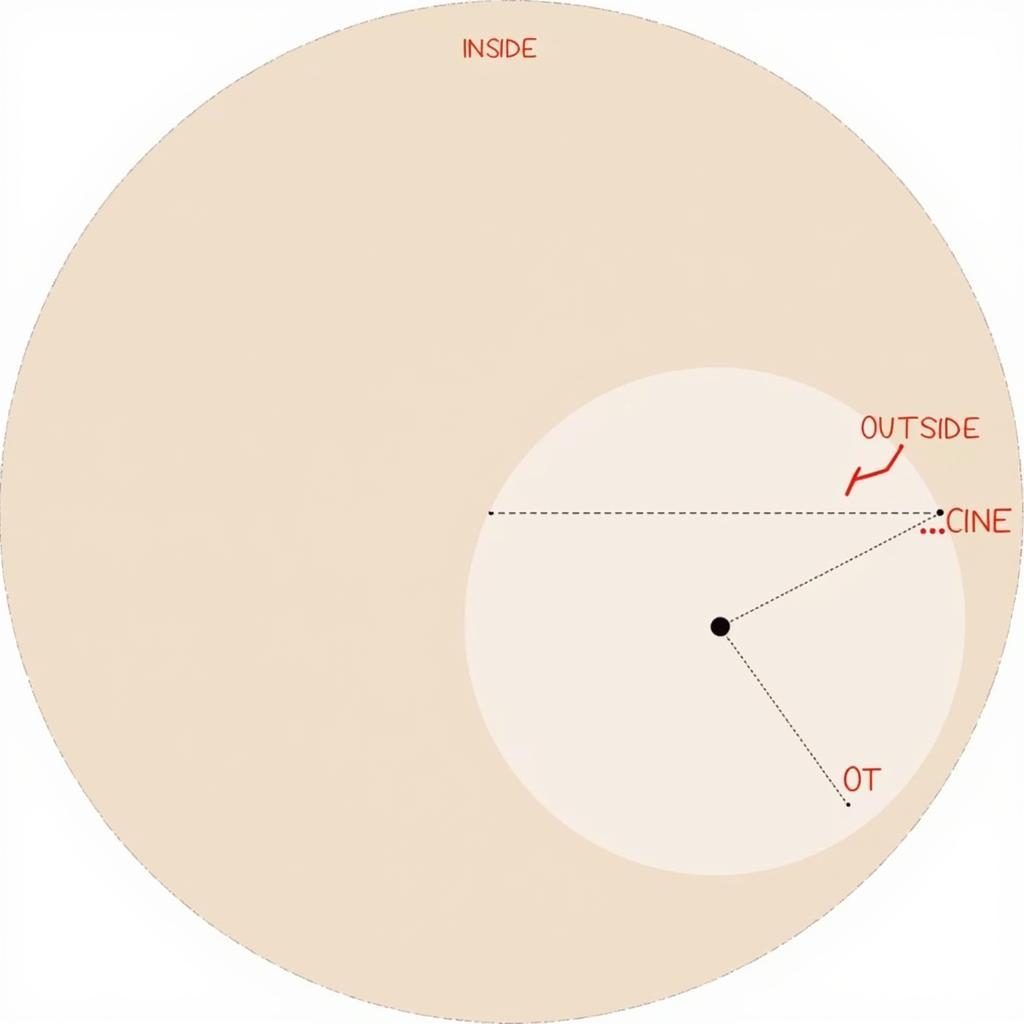Vị trí tương đối giữa điểm và đường tròn
2.3. Vị Trí Tương Đối Giữa Đường Thẳng Và Đường Tròn
- Đường thẳng cắt đường tròn: Đường thẳng có hai điểm chung với đường tròn.
- Đường thẳng tiếp xúc đường tròn: Đường thẳng có một điểm chung với đường tròn.
- Đường thẳng không cắt đường tròn: Đường thẳng không có điểm chung nào với đường tròn.
Bài Tập Áp Dụng Giải Toán 9 Hình Học Chương 1
Bài 1: Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Tính độ dài BC, đường cao AH, và các tỉ số lượng giác của góc B.
Bài 2: Cho đường tròn (O; R) và một điểm A nằm ngoài đường tròn sao cho OA = 2R. Từ A kẻ hai tiếp tuyến AB, AC đến đường tròn (B, C là hai tiếp điểm). Chứng minh:
- Tam giác ABC đều.
- BC = R√3.
Bài 3: Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H. Chứng minh:
- Tứ giác BFEC nội tiếp.
- Góc AEF = góc ABC.
Kết Luận
Việc ôn tập giải toán 9 hình học chương 1 là rất quan trọng, giúp học sinh củng cố kiến thức và tự tin hơn khi bước vào các chương học tiếp theo. Bằng việc nắm vững các định nghĩa, định lý và làm bài tập áp dụng, các em sẽ từng bước chinh phục môn Toán hình học lớp 9 một cách hiệu quả.
FAQ
1. Làm thế nào để học tốt giải toán 9 hình học?
Để học tốt giải toán 9 hình học, bạn cần nắm vững các định nghĩa, định lý, tính chất và các dạng bài tập cơ bản. Bên cạnh đó, việc rèn luyện kỹ năng vẽ hình, tư duy logic và khả năng chứng minh là rất quan trọng.
2. Chương 1 toán hình 9 có khó không?
Chương 1 toán hình 9 là chương học cơ bản, cung cấp những kiến thức nền tảng cho các chương học tiếp theo. Nếu bạn chú ý nghe giảng, làm bài tập đầy đủ và thường xuyên ôn tập thì sẽ không gặp nhiều khó khăn.
Bạn Cần Hỗ Trợ?
Liên hệ ngay với chúng tôi:
- Số Điện Thoại: 02033846993
- Email: [email protected]
- Địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam
Chúng tôi có đội ngũ chăm sóc khách hàng 24/7 sẵn sàng hỗ trợ bạn!
Đừng quên tham khảo thêm bài giảng giải phẫu sinh lý động vật và bộ đề đọc hiểu có lời giải chi tiết để bổ sung kiến thức cho mình nhé!