Việc nắm vững Cách Giải Lim là nền tảng quan trọng trong giải tích toán học. Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan về cách giải lim, từ những kiến thức cơ bản nhất đến các kỹ thuật nâng cao, giúp bạn tự tin chinh phục mọi bài toán liên quan đến giới hạn.
Giới Thiệu Về Giới Hạn (Lim)
Giới hạn của một hàm số (lim) mô tả giá trị mà hàm số “tiến đến” khi biến số của nó “tiến đến” một giá trị nhất định. Hiểu rõ khái niệm này là bước đầu tiên để nắm vững cách giải lim. Việc tính toán giới hạn có thể đơn giản hoặc phức tạp, tùy thuộc vào dạng của hàm số.
Cách Giải Lim Cơ Bản
Đối với các hàm số đơn giản, việc tính giới hạn chỉ đơn giản là thay giá trị của biến số vào hàm số. Tuy nhiên, đối với các hàm số phức tạp hơn, ta cần sử dụng các kỹ thuật khác nhau. Một số phương pháp cơ bản bao gồm:
- Thay trực tiếp: Nếu hàm số xác định tại điểm cần tính giới hạn, ta có thể thay trực tiếp giá trị đó vào hàm số.
- Rút gọn: Nếu thay trực tiếp dẫn đến dạng vô định (như 0/0), ta cần rút gọn biểu thức trước khi tính giới hạn.
- Nhân liên hợp: Kỹ thuật này thường được sử dụng khi gặp căn thức trong biểu thức giới hạn.
Xem thêm bài tập lim nâng cao có lời giải để tìm hiểu thêm.
Kỹ Thuật Giải Lim Nâng Cao
Khi gặp các bài toán lim phức tạp hơn, ta cần sử dụng các kỹ thuật nâng cao như:
- Định lý kẹp: Kỹ thuật này cho phép ta xác định giới hạn của một hàm số bằng cách “kẹp” nó giữa hai hàm số khác có cùng giới hạn.
- Quy tắc L’Hôpital: Quy tắc này được sử dụng để tính giới hạn của dạng vô định bằng cách lấy đạo hàm của tử số và mẫu số.
- Sử dụng giới hạn cơ bản: Nắm vững các giới hạn cơ bản sẽ giúp bạn giải quyết nhiều bài toán phức tạp hơn.
“Hiểu rõ các kỹ thuật giải lim nâng cao sẽ mở ra cánh cửa cho việc giải quyết các bài toán phức tạp trong giải tích.” – Nguyễn Văn A, Giảng viên Toán học
Cách Giải Giới Hạn Lim Với Hàm Lượng Giác
Các bài toán lim liên quan đến hàm lượng giác thường yêu cầu sự kết hợp giữa các kỹ thuật giải lim và các công thức lượng giác. Việc nắm vững các công thức lượng giác cơ bản và các giới hạn lượng giác đặc biệt là rất quan trọng.
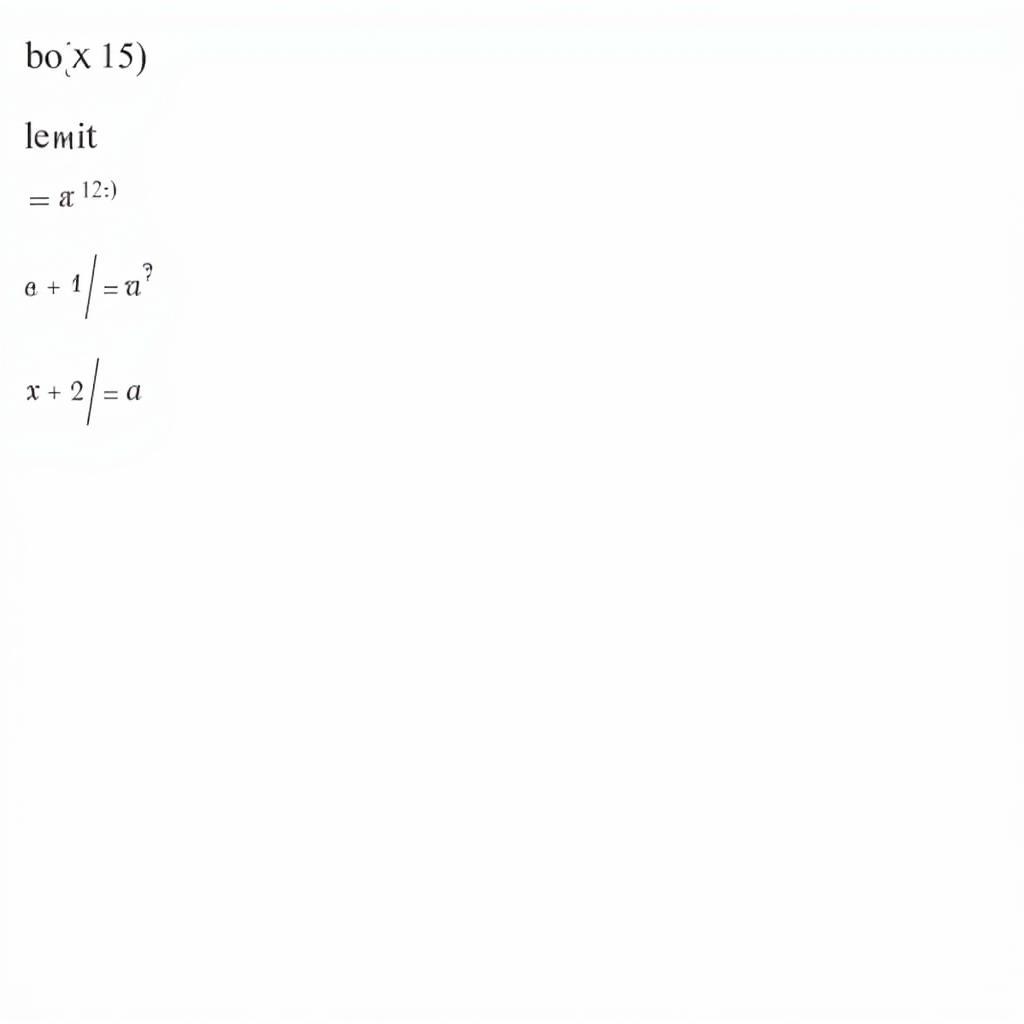Giải lim hàm lượng giác
Tham khảo thêm cách giải giới hạn lim để có cái nhìn chi tiết hơn.
Kết Luận
Nắm vững cách giải lim là chìa khóa để thành công trong giải tích toán học. Bài viết này đã cung cấp cho bạn một cái nhìn tổng quan về các phương pháp giải lim, từ cơ bản đến nâng cao. Hãy luyện tập thường xuyên để nâng cao kỹ năng của mình. Cũng đừng quên xem bị limited 180 ngày và cách giải quyết nếu bạn gặp vấn đề này.
FAQ
- Lim là gì?
- Cách tính lim của hàm số đơn giản?
- Khi nào nên sử dụng quy tắc L’Hôpital?
- Làm thế nào để giải lim với hàm lượng giác?
- Tài liệu nào giúp tôi luyện tập thêm về cách giải lim?
- Giới hạn của một dãy số là gì?
- Sự khác biệt giữa giới hạn của hàm số và giới hạn của dãy số là gì?
Các tình huống thường gặp câu hỏi về cách giải lim
- Không xác định được dạng vô định
- Áp dụng sai quy tắc L’Hôpital
- Quên các giới hạn lượng giác đặc biệt
Gợi ý các câu hỏi khác
- Cách tìm giới hạn của hàm số khi x tiến đến vô cùng?
- Ứng dụng của giới hạn trong thực tế là gì?
Tham khảo thêm bài giải chi tiết học kỳ 2 lớp 9 và giải hóa 12 cơ bản cho các kiến thức bổ trợ.
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.