Giải Phương Trình Logarit Bằng Phương Pháp Hàm Số là một kỹ thuật quan trọng trong giải tích. Phương pháp này tận dụng tính chất của hàm số để biến đổi và giải quyết các phương trình logarit phức tạp. Xem xét bài viết dưới đây để hiểu rõ hơn về phương pháp này. Ngay sau đoạn mở đầu này, chúng ta sẽ đi sâu vào chi tiết. bài 3 chương 1 giải tích 11
Phương Pháp Hàm Số: Khái Niệm Cơ Bản
Phương pháp hàm số trong giải phương trình logarit dựa trên việc biến đổi phương trình về dạng f(x) = g(x), trong đó f(x) và g(x) là hai hàm số. Sau đó, ta khảo sát tính đơn điệu của hai hàm số này để tìm ra nghiệm của phương trình. Việc nắm vững kiến thức về đạo hàm và bảng biến thiên là rất cần thiết để áp dụng phương pháp này hiệu quả.
Các Bước Giải Phương Trình Logarit Bằng Phương Pháp Hàm Số
Để giải phương trình logarit bằng phương pháp hàm số, ta thực hiện các bước sau:
- Biến đổi phương trình: Chuyển phương trình về dạng f(x) = g(x).
- Khảo sát hàm số: Xét tính đơn điệu của f(x) và g(x) bằng cách tính đạo hàm và lập bảng biến thiên.
- Tìm nghiệm: Dựa vào bảng biến thiên của hai hàm số, tìm giá trị của x sao cho f(x) = g(x).
- Kiểm tra nghiệm: Kiểm tra xem nghiệm tìm được có thỏa mãn điều kiện xác định của phương trình logarit ban đầu hay không.
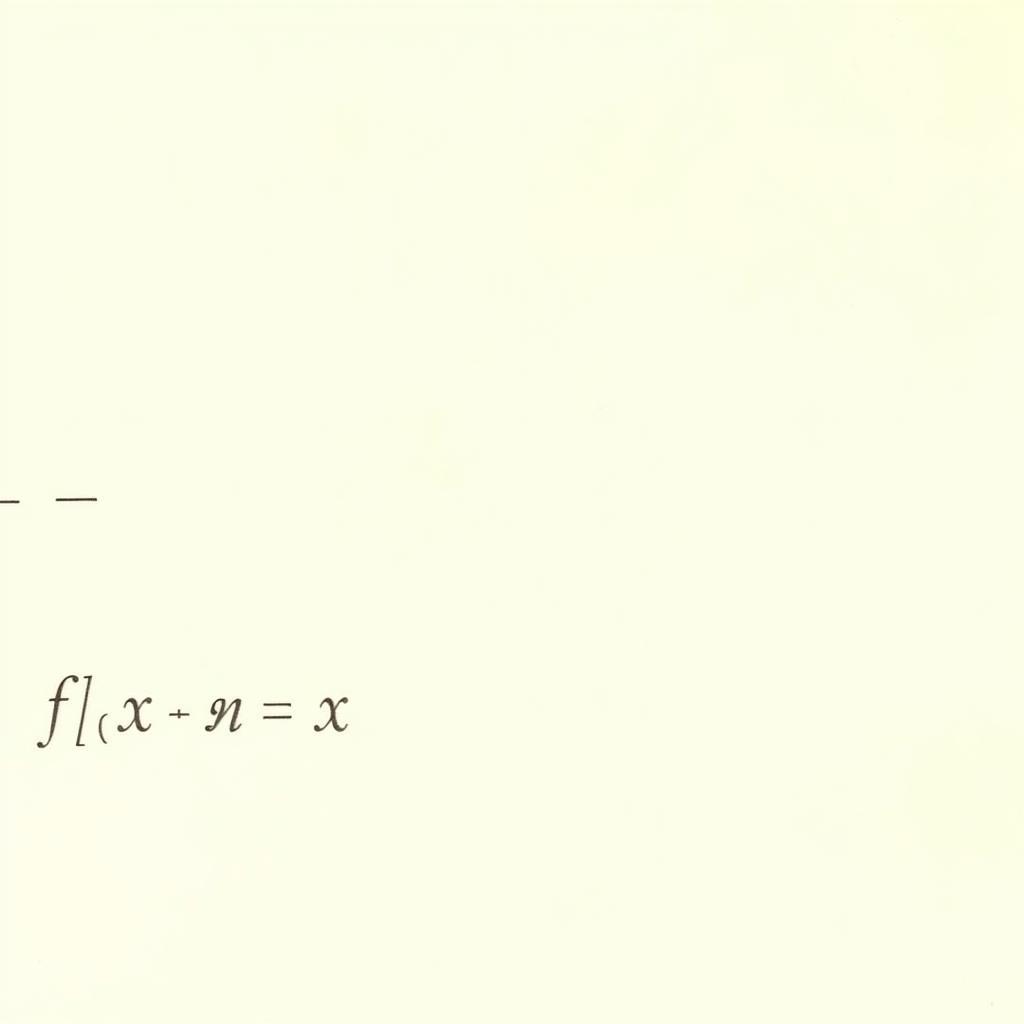 Biến đổi phương trình logarit
Biến đổi phương trình logarit
Ví Dụ Giải Phương Trình Logarit Bằng Phương Pháp Hàm Số
Giả sử ta cần giải phương trình: log₂(x + 1) = x – 1.
- Biến đổi: Phương trình đã có dạng f(x) = g(x) với f(x) = log₂(x + 1) và g(x) = x – 1.
- Khảo sát: f'(x) = 1/((x+1)ln2) > 0 với x > -1. Vậy f(x) đồng biến trên khoảng (-1, +∞). g'(x) = 1 > 0. Vậy g(x) đồng biến trên R.
- Tìm nghiệm: Nhận thấy f(1) = log₂(2) = 1 và g(1) = 1 – 1 = 0. f(2) = log₂(3) và g(2) = 2 – 1 = 1. Do đó, phương trình có nghiệm x = 2.
- Kiểm tra: x = 2 thỏa mãn điều kiện x > -1. Vậy nghiệm của phương trình là x = 2.
 Bảng biến thiên của hàm số logarit
Bảng biến thiên của hàm số logarit
Khi Nào Nên Sử Dụng Phương Pháp Hàm Số?
Phương pháp hàm số thường được sử dụng khi phương trình logarit không thể giải bằng các phương pháp thông thường như đưa về cùng cơ số hoặc sử dụng tính chất của logarit. giải bài tập toán 12 nguyên hàm Đặc biệt, phương pháp này hữu ích khi phương trình chứa cả logarit và hàm mũ hoặc các hàm số khác. bài 4 chương 2 giải tích 12
Kết Luận
Giải phương trình logarit bằng phương pháp hàm số là một công cụ mạnh mẽ giúp ta giải quyết các bài toán phức tạp. Việc nắm vững phương pháp này sẽ giúp bạn nâng cao khả năng giải toán và đạt kết quả tốt hơn trong học tập.
FAQ
- Phương pháp hàm số có áp dụng được cho mọi loại phương trình logarit không?
- Làm thế nào để xác định tính đơn điệu của hàm số?
- Có những phương pháp nào khác để giải phương trình logarit?
- Tại sao cần kiểm tra nghiệm sau khi giải bằng phương pháp hàm số?
- Khi nào nên sử dụng phương pháp đồ thị để giải phương trình logarit?
- Phương pháp hàm số có liên quan gì đến đạo hàm?
- Có tài liệu nào giúp tôi luyện tập thêm về phương pháp này không?
Mô tả các tình huống thường gặp câu hỏi.
Nhiều học sinh gặp khó khăn trong việc biến đổi phương trình logarit về dạng f(x) = g(x) hoặc trong việc khảo sát hàm số. Việc luyện tập thường xuyên với các bài tập đa dạng sẽ giúp khắc phục những khó khăn này.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về bài 1 trang 77 giải tích 12 hoặc 3.2 giải pháp nâng cao chất lượng thông tin trên trang web của chúng tôi.
