Bài 39 trang 52 sách giáo khoa Toán 8 mở ra cánh cửa vào thế giới hình học với những kiến thức quan trọng về diện tích hình thang và hình bình hành. Nắm vững các công thức và cách áp dụng chúng là chìa khóa để giải quyết các bài toán liên quan đến diện tích.
Diện tích Hình Thang: Công Thức và Ứng Dụng
Diện tích hình thang được tính bằng nửa tổng hai đáy nhân với chiều cao. Công thức này có thể được viết tắt là S = (a + b) h / 2, trong đó S là diện tích, a và b là độ dài hai đáy, và h là chiều cao của hình thang. Việc hiểu rõ công thức này là bước đầu tiên để giải quyết các bài toán liên quan. Ví dụ, nếu một hình thang có đáy lớn 5cm, đáy nhỏ 3cm, và chiều cao 4cm, diện tích của nó sẽ là (5 + 3) 4 / 2 = 16cm².
Việc áp dụng công thức tính diện tích hình thang có thể giúp chúng ta giải quyết nhiều bài toán thực tế, chẳng hạn như tính diện tích mảnh đất hình thang, tính diện tích tường nhà hình thang, hay tính diện tích các vật dụng có hình dạng tương tự.
Diện tích Hình Bình Hành: Công Thức và Ứng Dụng trong Giải Toán 8 Bài 39 Trang 52
Diện tích hình bình hành được tính bằng tích của cạnh đáy và chiều cao tương ứng. Công thức này có thể được viết tắt là S = a h, trong đó S là diện tích, a là độ dài cạnh đáy, và h là chiều cao tương ứng với cạnh đáy đó. Giải toán 8 bài 39 trang 52 sẽ yêu cầu học sinh áp dụng thành thạo công thức này. Ví dụ, một hình bình hành có cạnh đáy 6cm và chiều cao 4cm sẽ có diện tích là 6 4 = 24cm².
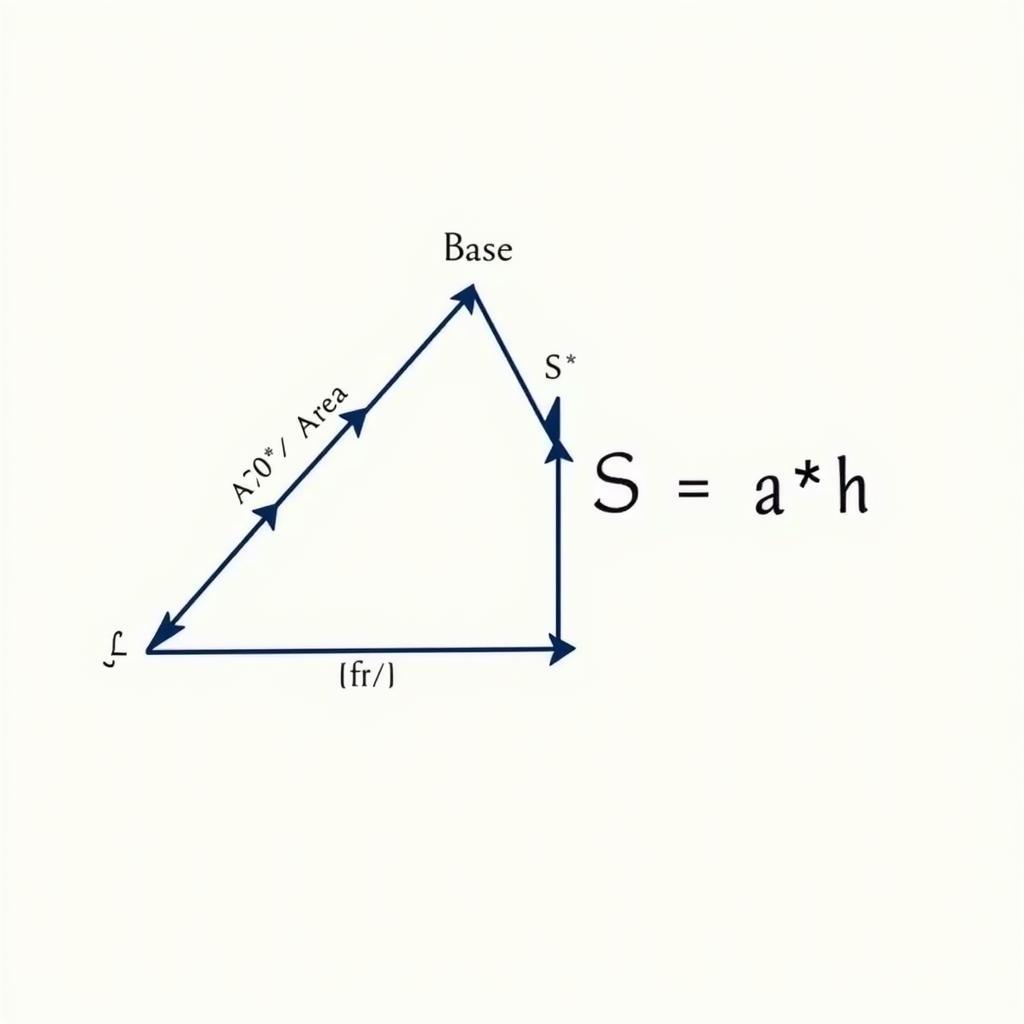Minh Họa Diện Tích Hình Bình Hành
Giống như hình thang, kiến thức về diện tích hình bình hành cũng có nhiều ứng dụng thực tiễn.
Bạn đã xem giải bài tập toán 2 chưa?
Mối Liên Hệ Giữa Hình Thang và Hình Bình Hành
Hình bình hành có thể được coi là một trường hợp đặc biệt của hình thang, khi hai đáy của hình thang bằng nhau. Điều này có nghĩa là công thức tính diện tích hình bình hành cũng có thể được suy ra từ công thức tính diện tích hình thang.
Chuyên gia toán học Nguyễn Văn A chia sẻ: “Hiểu rõ mối quan hệ giữa hình thang và hình bình hành sẽ giúp học sinh nắm vững kiến thức hình học một cách tổng quát hơn.”
Bạn muốn tìm hiểu thêm về giải bài tập hóa 9 trang 122?
Kết luận
Giải Toán 8 Bài 39 Trang 52 tập trung vào việc áp dụng công thức tính diện tích hình thang và hình bình hành. Nắm vững các công thức này và hiểu rõ mối quan hệ giữa hai hình này là chìa khóa để giải quyết các bài toán liên quan. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết để chinh phục bài học này.
FAQ
- Công thức tính diện tích hình thang là gì?
- Công thức tính diện tích hình bình hành là gì?
- Mối quan hệ giữa hình thang và hình bình hành là gì?
- Làm thế nào để áp dụng công thức tính diện tích hình thang vào bài toán thực tế?
- Làm thế nào để áp dụng công thức tính diện tích hình bình hành vào bài toán thực tế?
- Bài 39 trang 52 sách giáo khoa Toán 8 nói về nội dung gì?
- Có những dạng bài tập nào thường gặp trong bài 39 trang 52?
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn trong việc phân biệt chiều cao của hình thang và hình bình hành, cũng như áp dụng công thức vào các bài toán có hình vẽ phức tạp.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tham khảo giải toán lớp 2 trang 85 để ôn tập lại kiến thức cơ bản về hình học.