Giải Bài Tập Xác Suất Thống Kê Chương 7 là một bước quan trọng để nắm vững các kiến thức nền tảng của xác suất thống kê. Chương 7 thường tập trung vào các phân phối xác suất quan trọng và việc áp dụng chúng trong thực tế. Việc giải các bài tập này không chỉ giúp sinh viên ôn tập lý thuyết mà còn rèn luyện kỹ năng phân tích và giải quyết vấn đề.
Các Phân Phối Xác Suất Quan Trọng trong Chương 7
Chương 7 thường giới thiệu các phân phối xác suất quan trọng như phân phối chuẩn, phân phối Poisson, phân phối nhị thức, và phân phối mũ. Mỗi phân phối này có những đặc điểm và ứng dụng riêng. Việc hiểu rõ các đặc điểm này là chìa khóa để giải quyết các bài tập liên quan. Ví dụ, phân phối chuẩn thường được sử dụng để mô hình hóa các hiện tượng tự nhiên, trong khi phân phối Poisson được sử dụng để mô hình hóa số sự kiện xảy ra trong một khoảng thời gian hoặc không gian nhất định. Bạn đã bao giờ tự hỏi về logic đằng sau dự đoán tỷ số bóng đá? cách giải đen cờ bạc có thể cho bạn thấy một góc nhìn khác về xác suất.
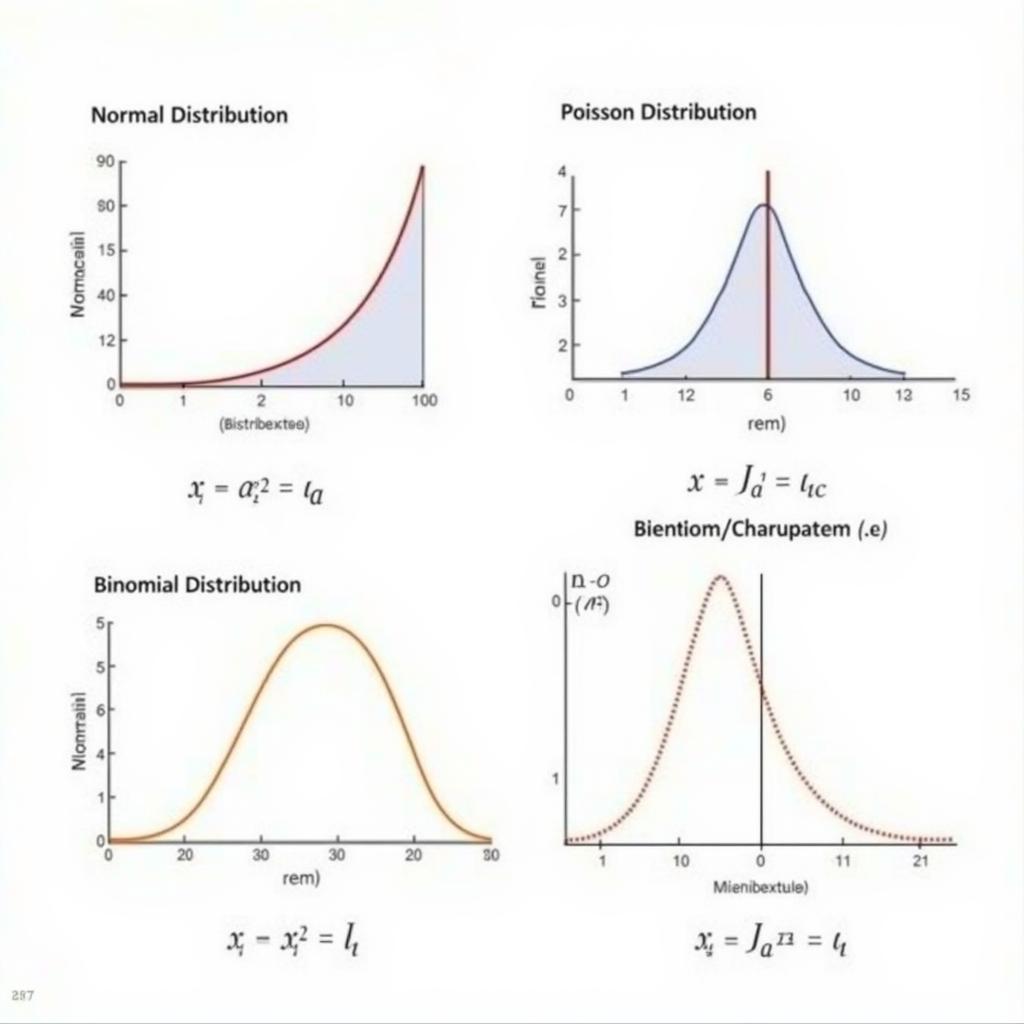Phân Phối Xác Suất Quan Trọng
Phương Pháp Giải Bài Tập Xác Suất Thống Kê Chương 7
Để giải quyết hiệu quả các bài tập xác suất thống kê chương 7, cần nắm vững các phương pháp sau:
- Xác định phân phối: Bước đầu tiên là xác định phân phối xác suất phù hợp với bài toán. Điều này đòi hỏi sự hiểu biết về đặc điểm của từng phân phối.
- Áp dụng công thức: Sau khi xác định được phân phối, cần áp dụng các công thức tương ứng để tính toán các đại lượng cần thiết, chẳng hạn như xác suất, kỳ vọng, phương sai.
- Kiểm tra kết quả: Luôn kiểm tra kết quả để đảm bảo tính chính xác và hợp lý.
Việc luyện tập thường xuyên với các bài tập đa dạng sẽ giúp bạn thành thạo các phương pháp này. Kiến thức về xác suất thống kê còn có thể được áp dụng trong nhiều lĩnh vực khác, ví dụ như phân tích dữ liệu trong kiến trúc. bài giải sách what are current trend in architecture cung cấp những phân tích sâu sắc về xu hướng kiến trúc hiện đại.
Ví Dụ Giải Bài Tập
Giả sử một biến ngẫu nhiên X tuân theo phân phối Poisson với tham số λ = 2. Tính xác suất P(X = 3).
Giải:
Áp dụng công thức phân phối Poisson: P(X = k) = (e^(-λ) * λ^k) / k!
Ta có: P(X = 3) = (e^(-2) * 2^3) / 3! ≈ 0.18
Việc hiểu rõ cấu trúc dữ liệu và giải thuật cũng rất quan trọng trong việc xử lý các bài toán xác suất thống kê. cấu trúc dữ liệu và giải thuật là gì sẽ giúp bạn tìm hiểu thêm về chủ đề này.
Kết Luận
Giải bài tập xác suất thống kê chương 7 là một quá trình quan trọng để nắm vững các kiến thức và kỹ năng cần thiết. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích về các phân phối xác suất quan trọng, phương pháp giải bài tập, và ví dụ minh họa. Chúc bạn thành công trong việc học tập và áp dụng xác suất thống kê!
Kết Luận Bài Viết
FAQ
- Phân phối chuẩn là gì?
- Phân phối Poisson được ứng dụng trong những trường hợp nào?
- Làm thế nào để xác định phân phối phù hợp với bài toán?
- Công thức tính kỳ vọng của phân phối nhị thức là gì?
- Phương sai của phân phối mũ được tính như thế nào?
- Tôi có thể tìm thêm bài tập ở đâu?
- Tài liệu nào giúp tôi học tốt chương 7?
Mô tả các tình huống thường gặp câu hỏi.
Sinh viên thường gặp khó khăn trong việc xác định phân phối phù hợp với bài toán và áp dụng đúng công thức. Việc luyện tập thường xuyên với các dạng bài tập khác nhau là cách tốt nhất để khắc phục khó khăn này. bài giảng toán cao cấp giải tích có thể hữu ích cho bạn.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các chủ đề liên quan như kiểm định giả thuyết, ước lượng khoảng tin cậy, và phân tích hồi quy. bản giải trình quy trình sản xuất cũng là một bài viết thú vị khác trên trang web.