Bài Tập Về Khoảng Cách Lớp 11 Có Lời Giải

Puskasvào
Hình ảnh minh họa khoảng cách từ điểm M đến mặt phẳng (P) trong không gian 3 chiều

Bài tập về khoảng cách lớp 11 là một phần quan trọng trong chương trình toán học, giúp học sinh phát triển tư duy hình học không gian và khả năng giải quyết vấn đề. Việc nắm vững các công thức và phương pháp tính khoảng cách giữa điểm với điểm, điểm với đường thẳng, điểm với mặt phẳng, đường thẳng với đường thẳng, đường thẳng với mặt phẳng và mặt phẳng với mặt phẳng là rất cần thiết để giải quyết các bài toán này. Bài viết này sẽ cung cấp cho bạn những lời giải chi tiết cho các dạng bài tập về khoảng cách lớp 11, giúp bạn hiểu rõ hơn về chủ đề này. Bạn sẽ tìm thấy các ví dụ minh họa, bài tập thực hành và lời giải chi tiết, từ đó nắm vững kiến thức và tự tin hơn khi đối mặt với các bài toán khó. Hãy cùng khám phá thế giới toán học đầy thú vị này!

Khoảng Cách Giữa Hai Điểm Trong Không Gian

Công thức tính khoảng cách giữa hai điểm A(x1, y1, z1) và B(x2, y2, z2) trong không gian Oxyz được xác định bởi: AB = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]. Đây là một công thức cơ bản và quan trọng, là nền tảng cho việc tính toán các loại khoảng cách khác trong không gian. Ví dụ, nếu A(1, 2, 3) và B(4, 5, 6), thì AB = √[(4-1)2 + (5-2)2 + (6-3)2] = √27 = 3√3. Cần lưu ý áp dụng đúng công thức và tính toán cẩn thận để tránh sai sót. Bạn có thể tham khảo thêm giải toán 9 tập 2 trang 19 để củng cố kiến thức về hệ tọa độ.

Khoảng Cách Từ Một Điểm Đến Một Mặt Phẳng

Công thức tính khoảng cách

Để tính khoảng cách từ một điểm M(x0, y0, z0) đến mặt phẳng (P): Ax + By + Cz + D = 0, ta sử dụng công thức: d(M, (P)) = |Ax0 + By0 + Cz0 + D| / √(A2 + B2 + C2). Ví dụ, tính khoảng cách từ điểm M(1, 2, 3) đến mặt phẳng (P): 2x – y + 2z + 1 = 0. Áp dụng công thức, ta có d(M, (P)) = |2(1) – 2 + 2(3) + 1| / √(22 + (-1)2 + 22) = 7/3. Cần phải nắm vững phương trình mặt phẳng và tọa độ điểm để áp dụng công thức một cách chính xác. Kiến thức về bài tập góc khoảng cách có lời giải cũng sẽ hữu ích trong việc giải quyết các bài toán liên quan.

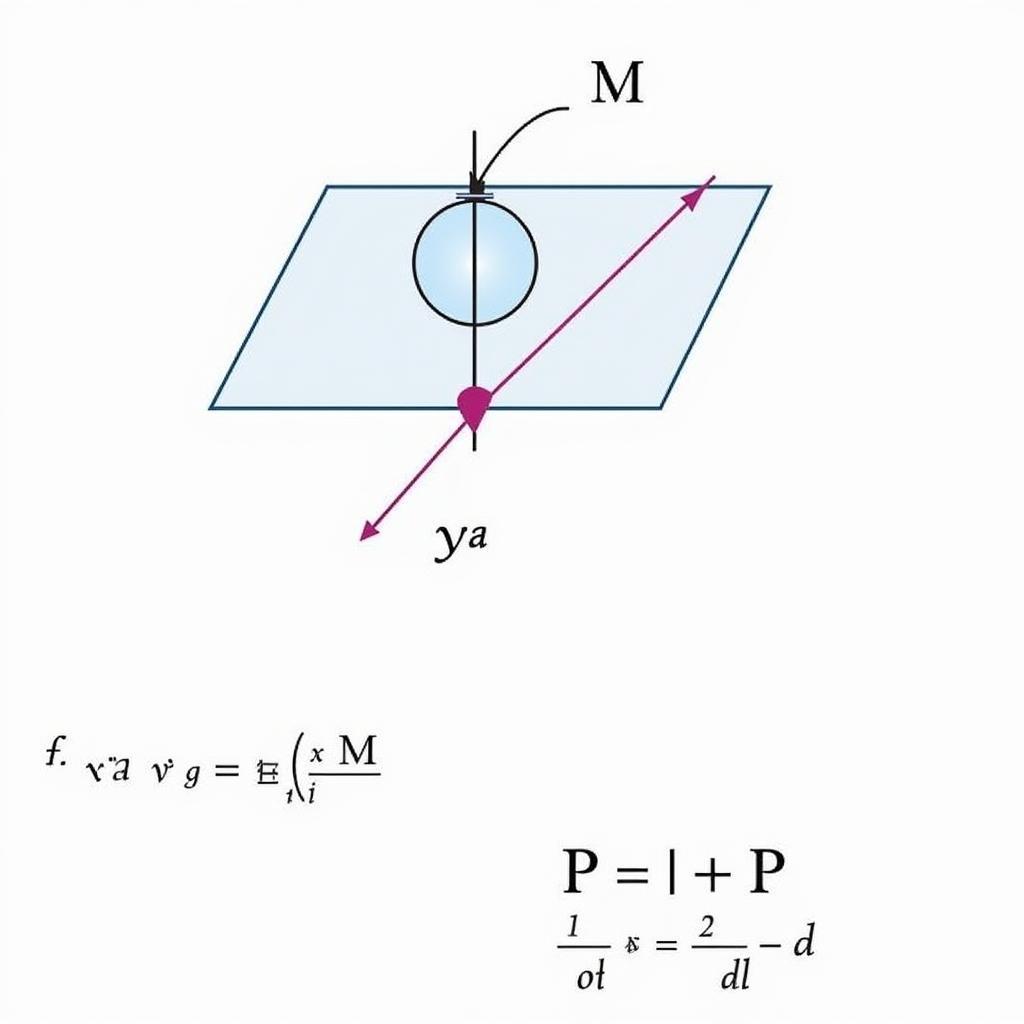Hình ảnh minh họa khoảng cách từ điểm M đến mặt phẳng (P) trong không gian 3 chiềuHình ảnh minh họa khoảng cách từ điểm M đến mặt phẳng (P) trong không gian 3 chiều

Ví dụ bài tập và lời giải

Bài tập: Tính khoảng cách từ điểm A(1, -2, 3) đến mặt phẳng (P): 2x + y – 2z + 5 = 0.

Lời giải: Áp dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng, ta có: d(A, (P)) = |2(1) + (-2) – 2(3) + 5| / √(22 + 12 + (-2)2) = |2 – 2 – 6 + 5| / √9 = |-1|/3 = 1/3.

Nguyễn Văn An, giáo viên Toán tại trường THPT chuyên Hạ Long, chia sẻ: “Việc luyện tập thường xuyên các dạng bài tập về khoảng cách là rất quan trọng để học sinh lớp 11 nắm vững kiến thức hình học không gian. Học sinh nên bắt đầu từ những bài toán cơ bản rồi dần dần nâng cao độ khó.”

Khoảng Cách Giữa Hai Đường Thẳng Chéo Nhau

Để tính khoảng cách giữa hai đường thẳng chéo nhau, ta cần xác định đường vuông góc chung của hai đường thẳng đó. Khoảng cách giữa hai đường thẳng chéo nhau chính là độ dài đoạn vuông góc chung. Bài toán này thường phức tạp hơn và đòi hỏi sự kết hợp nhiều kiến thức hình học không gian. Tham khảo giải sgk hóa để rèn luyện tư duy logic và giải quyết vấn đề.

Kết luận

Bài viết đã cung cấp kiến thức cơ bản về Bài Tập Về Khoảng Cách Lớp 11 Có Lời Giải, bao gồm công thức và ví dụ minh họa cho từng dạng bài tập. Việc nắm vững các kiến thức này sẽ giúp bạn tự tin hơn khi giải quyết các bài toán hình học không gian.

FAQ

  1. Công thức tính khoảng cách giữa hai điểm trong không gian là gì?
  2. Làm thế nào để tính khoảng cách từ một điểm đến một mặt phẳng?
  3. Khoảng cách giữa hai đường thẳng chéo nhau được tính như thế nào?
  4. Làm thế nào để xác định đường vuông góc chung của hai đường thẳng chéo nhau?
  5. Có tài liệu nào cung cấp bài tập về khoảng cách lớp 11 có lời giải chi tiết không?
  6. giải bài địa lý lớp 9 có giúp ích gì cho việc học toán không?
  7. giải bài tập về thấu kính hội tụ lớp 9 liên quan gì đến bài tập khoảng cách không?

Gợi ý các câu hỏi khác, bài viết khác có trong web.

Bạn có thể tìm hiểu thêm về các bài tập liên quan đến hình học không gian khác tại website của chúng tôi.

Khi cần hỗ trợ hãy liên hệ

Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.