Giải Toán 12 Bài 4 Chương 2 là chủ đề quan trọng giúp học sinh nắm vững kiến thức về hàm số lũy thừa, một dạng hàm số cơ bản trong chương trình toán học lớp 12. Bài viết này sẽ cung cấp cho bạn những kiến thức cần thiết để giải quyết các bài toán liên quan đến hàm số lũy thừa. Bạn sẽ tìm hiểu về định nghĩa, tính chất, đồ thị và cách ứng dụng hàm số lũy thừa vào các bài toán thực tế.
Định nghĩa và Tính chất của Hàm Số Lũy Thừa
Hàm số lũy thừa là hàm số có dạng y = xα, với α là một số thực. Tùy thuộc vào giá trị của α, hàm số lũy thừa sẽ có những tính chất khác nhau. Ví dụ, khi α là số nguyên dương, hàm số lũy thừa là một đa thức; khi α là số nguyên âm, hàm số lũy thừa là một hàm phân thức; khi α là số hữu tỉ, hàm số lũy thừa có thể được biểu diễn dưới dạng căn thức. Việc phân loại này rất quan trọng trong việc khảo sát và vẽ đồ thị hàm số lũy thừa. Bạn có thể tìm hiểu thêm về các dạng bài tập toán khác tại giải bài tập toán lớp 5 bài 48.
Một số tính chất quan trọng của hàm số lũy thừa cần nhớ là tính đơn điệu, tính liên tục, và tính khả vi. Tùy vào giá trị của α, hàm số lũy thừa có thể đồng biến hoặc nghịch biến trên tập xác định của nó. Hiểu rõ các tính chất này giúp ta dễ dàng giải quyết các bài toán liên quan đến so sánh, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lũy thừa. Tham khảo thêm về cách giải bài toán tìm giá trị lớn nhất và nhỏ nhất tại cách giải bài toán tìm gtln gtnn lớp 9.
Đồ Thị Hàm Số Lũy Thừa
Đồ thị hàm số lũy thừa có hình dạng khác nhau tùy thuộc vào giá trị của α. Khi α > 0, đồ thị đi qua gốc tọa độ và nằm phía trên trục hoành. Khi α < 0, đồ thị nằm phía trên trục hoành và có tiệm cận đứng là trục tung. Biết cách vẽ và phân tích đồ thị hàm số lũy thừa giúp ta hình dung rõ hơn về tính chất của hàm số và giải quyết các bài toán liên quan đến giao điểm, tiếp tuyến, v.v.
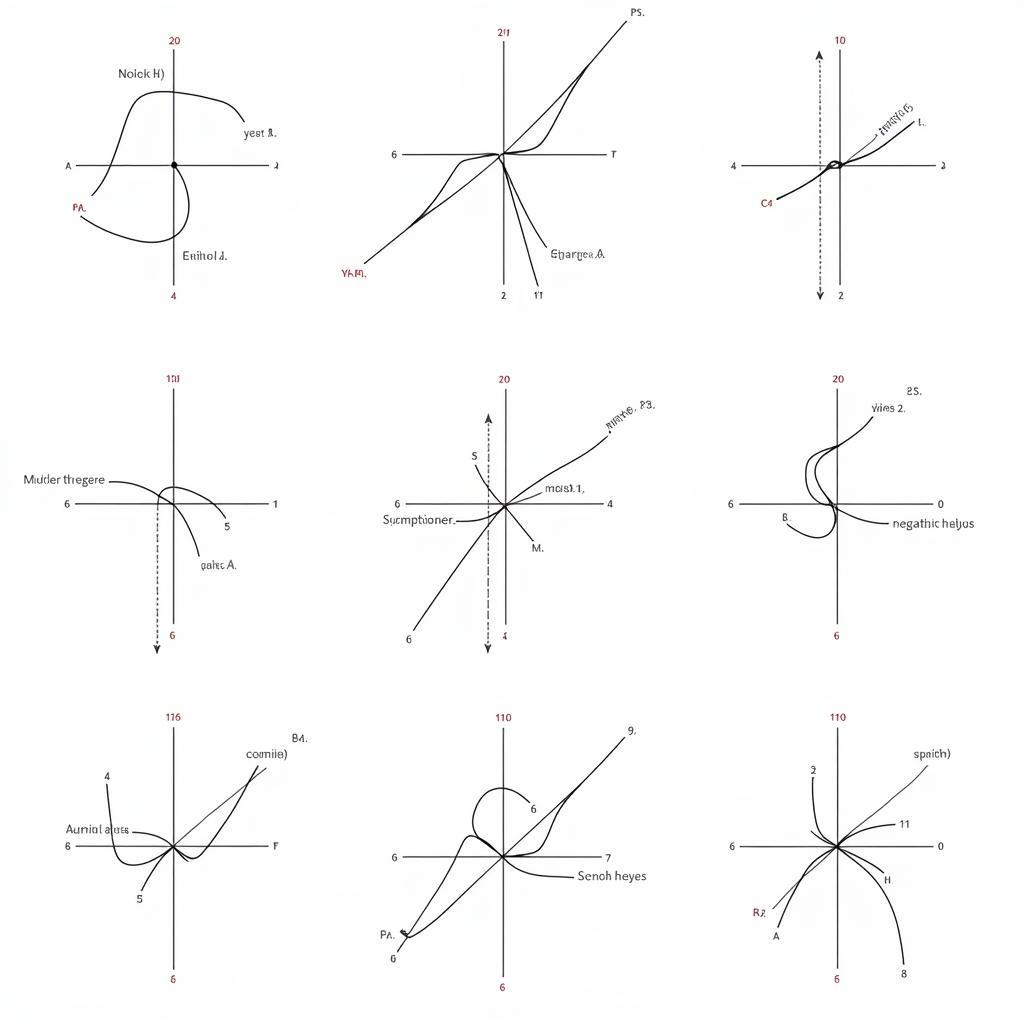Đồ thị hàm số lũy thừa
Ứng dụng của Hàm Số Lũy Thừa (Giải Toán 12 Bài 4 Chương 2)
Hàm số lũy thừa có nhiều ứng dụng trong thực tế, chẳng hạn như trong vật lý, kinh tế, và kỹ thuật. Ví dụ, trong vật lý, hàm số lũy thừa được sử dụng để mô tả sự phụ thuộc của năng lượng vào vận tốc; trong kinh tế, hàm số lũy thừa được sử dụng để mô tả sự tăng trưởng kinh tế. Còn rất nhiều ví dụ khác minh chứng cho tính ứng dụng rộng rãi của hàm số lũy thừa trong đời sống. Bạn có thể xem thêm các bài giải toán 8 tại giải toán 8 loigiaihay.
Kết luận
Giải toán 12 bài 4 chương 2 về hàm số lũy thừa là một phần quan trọng trong chương trình toán học lớp 12. Hiểu rõ định nghĩa, tính chất, đồ thị và ứng dụng của hàm số lũy thừa sẽ giúp bạn giải quyết các bài toán một cách hiệu quả.
Ứng dụng hàm số lũy thừa
FAQ
- Hàm số lũy thừa là gì?
- Tập xác định của hàm số lũy thừa là gì?
- Cách vẽ đồ thị hàm số lũy thừa như thế nào?
- Hàm số lũy thừa có những tính chất gì?
- Ứng dụng của hàm số lũy thừa trong thực tế là gì?
- Làm sao để phân biệt hàm số lũy thừa với các loại hàm số khác?
- Có những dạng bài tập nào thường gặp về hàm số lũy thừa?
Bạn muốn tìm hiểu thêm về giao thoa sóng cơ? Hãy xem bài tập về giao thoa sóng cơ có lời giải. Cần giải vở bài tập toán 9? giải vở bài tập toán lớp 9 tập 1 sẽ giúp bạn.
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.