Automat và ngôn ngữ hình thức là những khái niệm nền tảng trong khoa học máy tính, đặc biệt là trong lĩnh vực lý thuyết tính toán. Bài viết này sẽ cung cấp giải mẫu cho một số bài tập về automat và ngôn ngữ hình thức, giúp bạn hiểu rõ hơn về cách áp dụng lý thuyết vào thực tế.
Automat hữu hạn xác định (DFA)
Automat hữu hạn xác định (DFA) là một mô hình toán học được sử dụng để nhận dạng các chuỗi ký tự thuộc một ngôn ngữ nhất định. Một DFA bao gồm một tập hợp các trạng thái, một bảng chuyển trạng thái, một trạng thái bắt đầu và một tập hợp các trạng thái kết thúc.
Bài tập 1: Xây dựng DFA nhận dạng chuỗi nhị phân chứa số chẵn số 1
Yêu cầu: Xây dựng DFA nhận dạng các chuỗi nhị phân chứa số chẵn số 1.
Giải pháp:
- Trạng thái: Q = {q0, q1}
- Bảng chuyển trạng thái:
- δ(q0, 0) = q0
- δ(q0, 1) = q1
- δ(q1, 0) = q1
- δ(q1, 1) = q0
- Trạng thái bắt đầu: q0
- Trạng thái kết thúc: q0
DFA này bắt đầu ở trạng thái q0. Nếu đọc được số 0, nó vẫn ở trạng thái q0. Nếu đọc được số 1, nó chuyển sang trạng thái q1. Trạng thái q0 đại diện cho số chẵn số 1, và q1 đại diện cho số lẻ số 1.
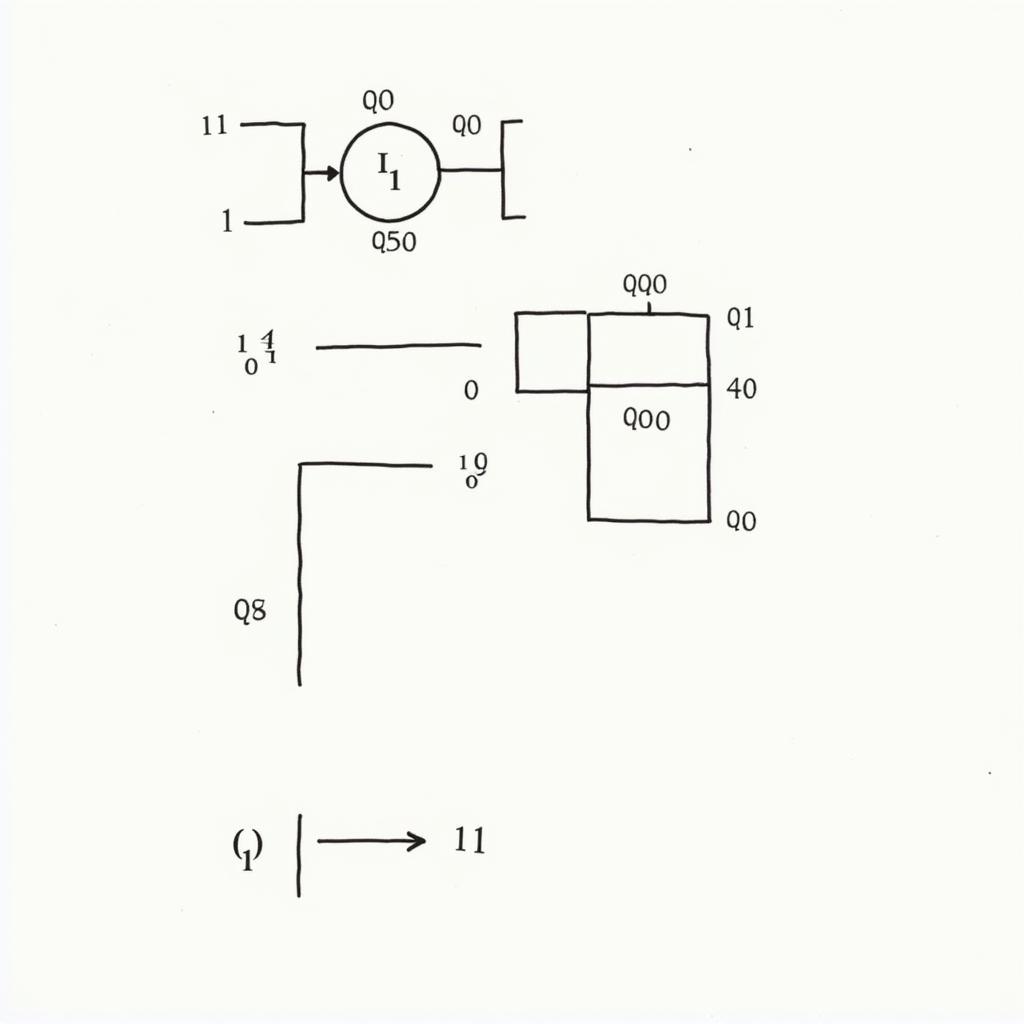DFA nhận dạng chuỗi nhị phân chứa số chẵn số 1
Ngôn ngữ hình thức
Ngôn ngữ hình thức là một tập hợp các chuỗi ký tự được xây dựng từ một bảng chữ cái nhất định. Có nhiều cách để mô tả ngôn ngữ hình thức, bao gồm biểu thức chính quy, ngữ pháp và automat.
Bài tập 2: Viết biểu thức chính quy cho ngôn ngữ gồm các chuỗi bắt đầu bằng ‘a’ và kết thúc bằng ‘b’
Yêu cầu: Viết biểu thức chính quy cho ngôn ngữ gồm các chuỗi bắt đầu bằng ‘a’ và kết thúc bằng ‘b’.
Giải pháp: a.*b
Biểu thức chính quy này sử dụng . để khớp với bất kỳ ký tự nào và * để khớp với 0 hoặc nhiều lần xuất hiện của ký tự trước đó. Do đó, a.*b sẽ khớp với bất kỳ chuỗi nào bắt đầu bằng ‘a’, theo sau là bất kỳ chuỗi ký tự nào, và kết thúc bằng ‘b’.
Ngữ pháp
Ngữ pháp là một tập hợp các quy tắc được sử dụng để tạo ra các chuỗi ký tự thuộc một ngôn ngữ nhất định. Ngữ pháp thường được sử dụng để mô tả cấu trúc cú pháp của ngôn ngữ lập trình.
Bài tập 3: Xây dựng ngữ pháp cho ngôn ngữ gồm các chuỗi palindromic
Yêu cầu: Xây dựng ngữ pháp cho ngôn ngữ gồm các chuỗi palindromic (chuỗi đọc xuôi hay ngược đều giống nhau) trên bảng chữ cái {a, b}.
Giải pháp:
- Biến: S
- Ký hiệu đầu cuối: a, b
- Quy tắc sản xuất:
- S -> ε
- S -> a
- S -> b
- S -> aSa
- S -> bSb
Ngữ pháp này cho phép tạo ra các chuỗi palindromic bằng cách thêm các ký tự giống nhau vào hai bên của biến S.
Kết luận
Bài viết này đã cung cấp Bài Tập Giải Mẫu Automat Và Ngôn Ngữ Hình Thức, bao gồm DFA, biểu thức chính quy và ngữ pháp. Hiểu rõ các khái niệm này là rất quan trọng cho việc học tập và nghiên cứu trong lĩnh vực khoa học máy tính.
FAQ
- Automat là gì?
- Ngôn ngữ hình thức là gì?
- Sự khác nhau giữa DFA và NFA là gì?
- Biểu thức chính quy được sử dụng để làm gì?
- Ngữ pháp được sử dụng để làm gì?
- Làm thế nào để chuyển đổi giữa các biểu diễn khác nhau của ngôn ngữ hình thức?
- Ứng dụng của automat và ngôn ngữ hình thức trong thực tế là gì?
Mô tả các tình huống thường gặp câu hỏi.
Người dùng thường gặp khó khăn trong việc xây dựng DFA, viết biểu thức chính quy và xây dựng ngữ pháp cho một ngôn ngữ nhất định. Việc hiểu rõ các định nghĩa và áp dụng các phương pháp giải quyết bài toán là chìa khóa để thành công.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các chủ đề liên quan như máy Turing, ngữ pháp Chomsky, và lý thuyết tính toán trên website “Giải Bóng”.