Giới hạn dãy số là một khái niệm quan trọng trong giải tích, giúp ta hiểu được hành vi của một dãy số khi số hạng tiến tới vô cùng. Bài viết này sẽ cung cấp cho bạn những kiến thức cơ bản về giới hạn dãy số, kèm theo các bài tập và lời giải chi tiết để bạn có thể nắm vững nội dung này. Chúng ta sẽ cùng nhau khám phá các phương pháp giải bài tập giới hạn dãy số, từ cơ bản đến nâng cao.
Bạn đang tìm kiếm những bài tập giới hạn dãy số có lời giải để luyện tập và nâng cao kỹ năng giải toán của mình? Vậy thì bài viết này chính là dành cho bạn. Chúng tôi sẽ cung cấp cho bạn những bài tập từ dễ đến khó, kèm theo lời giải chi tiết và những phân tích cụ thể để giúp bạn hiểu rõ hơn về giới hạn dãy số. Xem thêm bài viết về bài tập tìm hạng của ma trận có lời giải.
Khái Niệm Giới Hạn Dãy Số
Giới hạn của một dãy số là giá trị mà dãy số đó “tiến tới” khi chỉ số của các số hạng trong dãy tăng lên vô hạn. Nói cách khác, nếu một dãy số có giới hạn là L, thì các số hạng của dãy số đó sẽ càng ngày càng gần với L khi chỉ số của chúng càng lớn.
Các Phương Pháp Tìm Giới Hạn Dãy Số
Sử Dụng Định Nghĩa
Đây là phương pháp cơ bản nhất để tìm giới hạn dãy số. Tuy nhiên, phương pháp này thường khá phức tạp và ít được sử dụng trong thực tế.
Sử Dụng Các Định Lý Về Giới Hạn
Có nhiều định lý về giới hạn giúp ta tính toán giới hạn dãy số một cách dễ dàng hơn, ví dụ như định lý về giới hạn của tổng, hiệu, tích, thương của các dãy số.
Sử Dụng Kỹ Thuật Chia Cho Số Hạng Có Bậc Cao Nhất
Kỹ thuật này thường được áp dụng cho các dãy số có dạng phân thức.
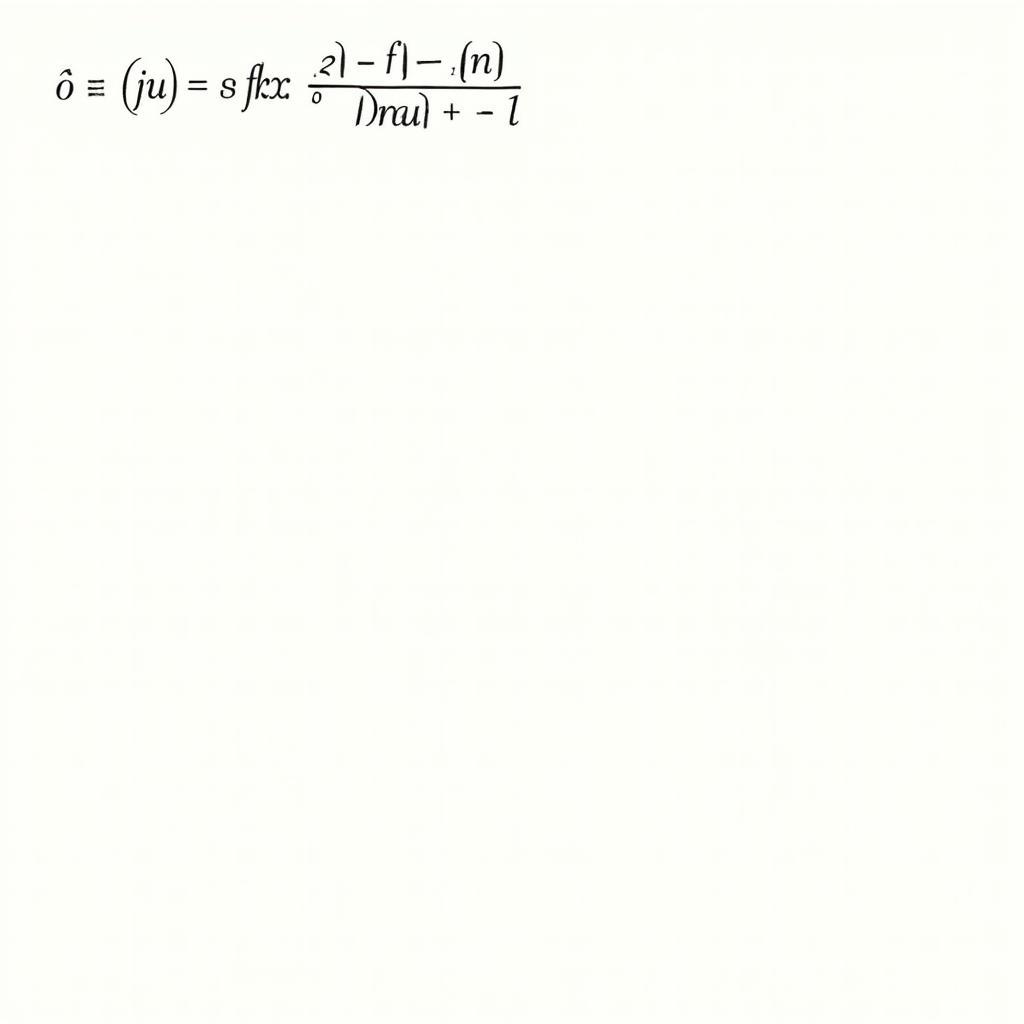 Bài tập giới hạn dãy số dạng phân thức
Bài tập giới hạn dãy số dạng phân thức
Bài Tập Giới Hạn Dãy Số Có Lời Giải
Bài Tập 1: Giới Hạn Hữu Hạn
Tìm giới hạn của dãy số un = (2n + 1) / (n + 3).
Lời giải: Chia cả tử và mẫu cho n, ta được un = (2 + 1/n) / (1 + 3/n). Khi n tiến tới vô cùng, 1/n và 3/n đều tiến tới 0. Do đó, giới hạn của dãy số là 2/1 = 2.
Bài Tập 2: Giới Hạn Vô Cùng
Tìm giới hạn của dãy số vn = n2 + 3n – 1.
Lời giải: Khi n tiến tới vô cùng, n2 cũng tiến tới vô cùng. Do đó, giới hạn của dãy số vn là vô cùng.
Bài Tập 3: Giới Hạn Dãy Số Chứa Căn
Tìm giới hạn của dãy số wn = √(n2 + 2n) – n.
Lời giải: Nhân liên hợp, ta được wn = (n2 + 2n – n2) / (√(n2 + 2n) + n) = 2n / (√(n2 + 2n) + n). Chia cả tử và mẫu cho n, ta được wn = 2 / (√(1 + 2/n) + 1). Khi n tiến tới vô cùng, 2/n tiến tới 0. Do đó, giới hạn của dãy số là 2 / (1 + 1) = 1. Nếu bạn quan tâm đến giải trí, hãy xem list truyện trọng sinh giới giải trí.
Trích dẫn từ chuyên gia Nguyễn Văn A, giảng viên Toán học tại Đại học Bách Khoa Hà Nội: “Việc luyện tập thường xuyên các bài tập giới hạn dãy số sẽ giúp sinh viên nắm vững kiến thức và áp dụng vào giải quyết các bài toán phức tạp hơn.”
Kết Luận
Bài Tập Giới Hạn Dãy Số Và Lời Giải là một phần quan trọng trong giải tích. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và bài tập hữu ích để nắm vững nội dung này. Hãy tiếp tục luyện tập để nâng cao kỹ năng giải toán của bạn. Xem thêm về ai đoạt giải olympic toán quốc tế.
FAQ
- Giới hạn dãy số là gì?
- Làm thế nào để tìm giới hạn của một dãy số?
- Kỹ thuật chia cho số hạng có bậc cao nhất được áp dụng khi nào?
- Giới hạn của dãy số có thể là vô cùng được không?
- Làm thế nào để tìm giới hạn của dãy số chứa căn?
- Tôi có thể tìm thêm bài tập ở đâu?
- Có tài liệu nào khác để học về giới hạn dãy số không?
Bạn muốn tìm hiểu thêm về âm nhạc? Hãy xem ca nhạc giải phóng remix.
Bạn muốn tìm hiểu về một bộ phim? Hãy xem gerald’s game giải thích.
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
