Phép tịnh tiến là một trong những phép biến hình quan trọng trong chương trình Toán lớp 11. Để giúp các em học sinh nắm vững kiến thức về phép tịnh tiến, bài viết này sẽ cung cấp hệ thống bài tập có lời giải chi tiết, từ cơ bản đến nâng cao, bám sát chương trình SGK.
Các dạng bài tập phép tịnh tiến lớp 11 thường gặp
Phần này sẽ giới thiệu các dạng bài tập phép tịnh tiến lớp 11 phổ biến, giúp học sinh làm quen và luyện tập nhuần nhuyễn.
Dạng 1: Xác định ảnh của một điểm, hình ảnh qua phép tịnh tiến
Đây là dạng bài tập cơ bản nhất, yêu cầu học sinh vận dụng trực tiếp định nghĩa và tính chất của phép tịnh tiến.
Ví dụ: Cho tam giác ABC và vectơ $overrightarrow{u}$. Tìm ảnh của tam giác ABC qua phép tịnh tiến theo vectơ $overrightarrow{u}$.
Lời giải:
Để tìm ảnh của tam giác ABC, ta tìm ảnh của từng đỉnh A, B, C qua phép tịnh tiến theo vectơ $overrightarrow{u}$.
- Gọi A’ là ảnh của A qua phép tịnh tiến theo vectơ $overrightarrow{u}$, ta có: $overrightarrow{AA’} = overrightarrow{u}$.
- Tương tự, ta tìm được ảnh B’ của B và ảnh C’ của C.
- Khi đó, tam giác A’B’C’ chính là ảnh của tam giác ABC qua phép tịnh tiến theo vectơ $overrightarrow{u}$.
Dạng 2: Tìm vectơ tịnh tiến
Dạng bài tập này yêu cầu học sinh vận dụng kiến thức về sự biến thiên của hình học tọa độ để tìm ra vectơ tịnh tiến.
Ví dụ: Cho đường thẳng d: 2x – y + 3 = 0. Tìm vectơ tịnh tiến biến đường thẳng d thành đường thẳng d’: 2x – y = 0.
Lời giải:
- Chọn một điểm A bất kỳ thuộc d, ví dụ A(0, 3).
- Tìm A’ là ảnh của A qua phép tịnh tiến biến d thành d’. Do d’ có phương trình 2x – y = 0 nên ta chọn A'(1, 2) thuộc d’.
- Khi đó, $overrightarrow{u} = overrightarrow{AA’} = (1, -1)$ là vectơ tịnh tiến cần tìm.
Dạng 3: Chứng minh tính chất هندسية của phép tịnh tiến
Dạng bài tập này thường yêu cầu học sinh vận dụng linh hoạt các tính chất của phép tịnh tiến, kết hợp với kiến thức về tam giác, đường thẳng, đường tròn…
Ví dụ: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng phép tịnh tiến theo vectơ $overrightarrow{MN}$ biến tam giác AMP thành tam giác CNP.
Lời giải:
- Ta có: $overrightarrow{MN} = overrightarrow{MA} + overrightarrow{AN}$ và $overrightarrow{MN} = overrightarrow{MC} + overrightarrow{CN}$.
- Do M, N lần lượt là trung điểm BC, CA nên $overrightarrow{MA} + overrightarrow{MC} = overrightarrow{0}$ và $overrightarrow{AN} + overrightarrow{CN} = overrightarrow{0}$.
- Từ đó, suy ra $overrightarrow{MP} = overrightarrow{MA} + overrightarrow{AP} = overrightarrow{CN} + overrightarrow{NP} = overrightarrow{CP}$.
- Vậy phép tịnh tiến theo vectơ $overrightarrow{MN}$ biến điểm M thành điểm C, điểm P thành điểm P, nên biến tam giác AMP thành tam giác CNP.
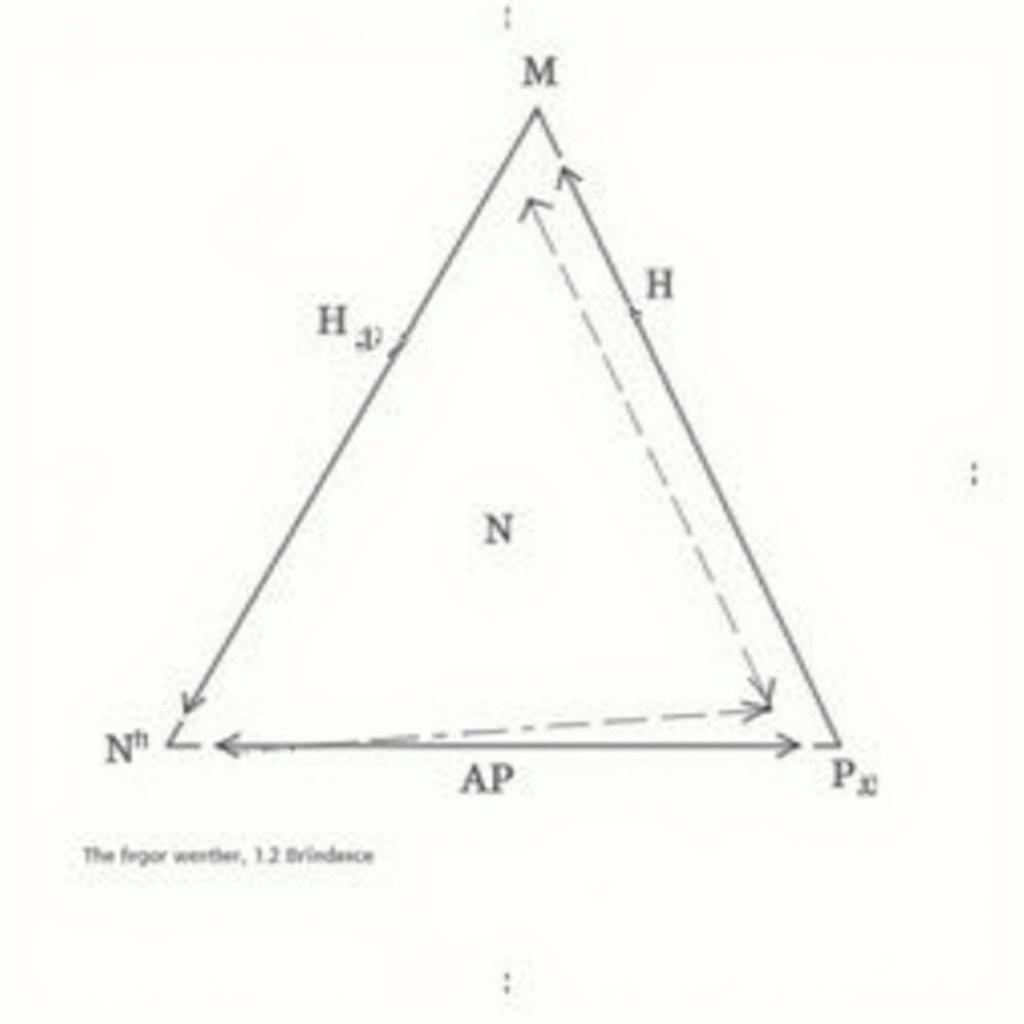Chứng minh tính chất
Mẹo ghi nhớ và vận dụng phép tịnh tiến hiệu quả
Để học tốt phép tịnh tiến, học sinh cần:
- Nắm vững định nghĩa, tính chất và biểu thức tọa độ của phép tịnh tiến.
- Rèn luyện kỹ năng vẽ hình, biểu diễn các yếu tố liên quan đến phép tịnh tiến trên mặt phẳng tọa độ.
- Luyện tập thường xuyên các dạng bài tập từ cơ bản đến nâng cao.
- Áp dụng linh hoạt các tính chất của phép tịnh tiến vào giải quyết các bài toán hình học phức tạp.
Kết luận
Phép tịnh tiến là một kiến thức quan trọng trong chương trình Toán lớp 11. Hy vọng rằng qua bài viết này, các em học sinh đã nắm vững được kiến thức về phép tịnh tiến và tự tin hơn khi giải các bài tập liên quan.
FAQs
1. Phép tịnh tiến có bảo toàn khoảng cách giữa hai điểm không?
Có. Phép tịnh tiến là một phép dời hình, do đó bảo toàn khoảng cách giữa hai điểm.
2. Làm thế nào để tìm ảnh của một đường thẳng qua phép tịnh tiến?
Chọn hai điểm bất kỳ thuộc đường thẳng đó, tìm ảnh của hai điểm đó qua phép tịnh tiến. Đường thẳng đi qua hai ảnh đó chính là ảnh của đường thẳng ban đầu.
3. Phép tịnh tiến có ứng dụng gì trong thực tế?
Phép tịnh tiến được ứng dụng trong nhiều lĩnh vực như kiến trúc, thiết kế, đồ họa máy tính, robot…
Bạn cần hỗ trợ?
Liên hệ ngay với Giải Bóng:
- Số Điện Thoại: 02033846993
- Email: [email protected]
- Địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam.
Đội ngũ chăm sóc khách hàng của chúng tôi luôn sẵn sàng hỗ trợ bạn 24/7!