Bài 73 trong sách giáo khoa Toán lớp 9, trang 40, đưa chúng ta đến với thế giới hình học không gian đầy thú vị. Bài học này tập trung vào việc hình thành khái niệm về đường thẳng vuông góc với mặt phẳng, một kiến thức nền tảng để giải quyết các bài toán phức tạp hơn về hình học không gian.
Điểm Mấu Chốt Của Đường Thẳng Vuông Góc Với Mặt Phẳng
Để hiểu rõ hơn về đường thẳng vuông góc với mặt phẳng, chúng ta cần nắm vững định nghĩa và tính chất của nó:
Định nghĩa: Một đường thẳng được gọi là vuông góc với một mặt phẳng khi nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
Tính chất:
- Qua một điểm cho trước, chỉ có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
- Qua một điểm cho trước, chỉ có duy nhất một đường thẳng vuông góc với một mặt phẳng cho trước.
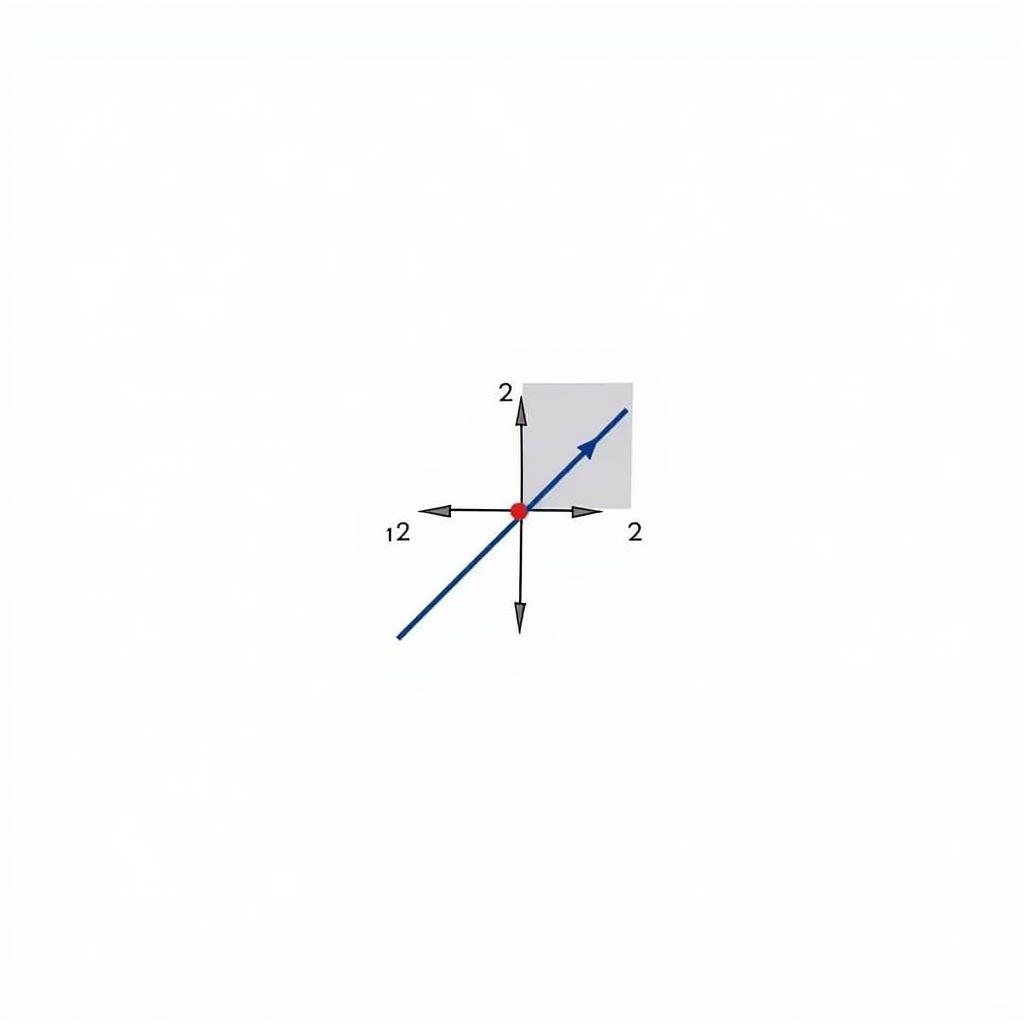 Đường thẳng vuông góc với mặt phẳng
Đường thẳng vuông góc với mặt phẳng
Cách Xác Định Đường Thẳng Vuông Góc Với Mặt Phẳng
Để xác định xem một đường thẳng có vuông góc với một mặt phẳng hay không, chúng ta có thể sử dụng một trong hai cách sau:
Cách 1: Chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
Cách 2: Sử dụng định lý ba đường vuông góc:
- Định lý: Cho đường thẳng a vuông góc với mặt phẳng (P) tại điểm O, và đường thẳng b nằm trong (P). Khi đó, nếu a vuông góc với hình chiếu của b lên (P) thì a vuông góc với b.
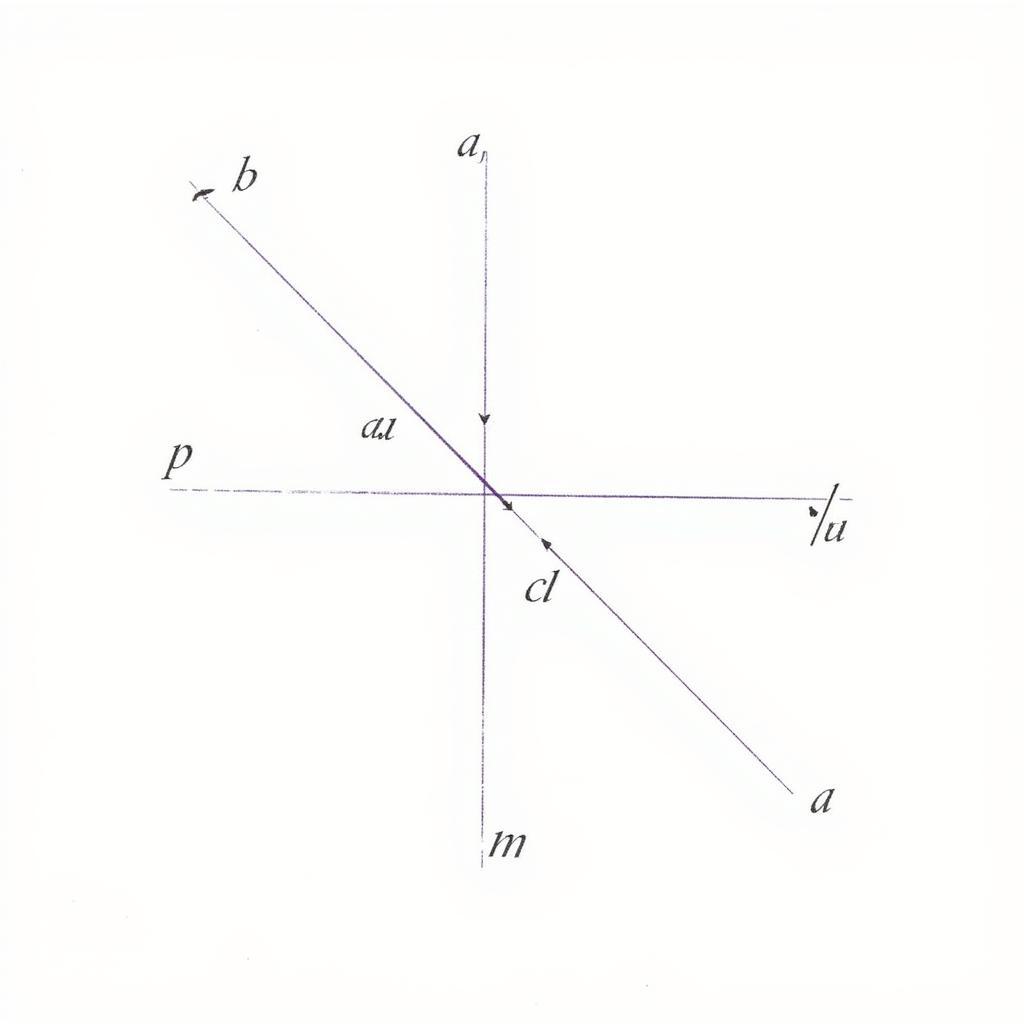 Minh họa định lý ba đường vuông góc
Minh họa định lý ba đường vuông góc
Ứng Dụng Của Đường Thẳng Vuông Góc Với Mặt Phẳng Trong Giải Toán 9 Bài 73 Trang 40
Bài tập trong bài 73, trang 40, sách giáo khoa Toán lớp 9 yêu cầu học sinh vận dụng kiến thức về đường thẳng vuông góc với mặt phẳng để giải quyết các vấn đề liên quan đến hình học không gian, chẳng hạn như:
- Xác định góc giữa đường thẳng và mặt phẳng.
- Tính khoảng cách từ một điểm đến một mặt phẳng.
- Chứng minh hai mặt phẳng vuông góc với nhau.
Kết Luận
Hiểu rõ về đường thẳng vuông góc với mặt phẳng là chìa khóa để giải quyết các bài toán hình học không gian trong chương trình Toán lớp 9, đặc biệt là bài 73 trang 40. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích và giúp bạn tự tin hơn trong việc chinh phục môn Toán.
