Hàm truyền đạt là một công cụ toán học quan trọng trong lĩnh vực điều khiển tự động, giúp mô tả mối quan hệ giữa đầu vào và đầu ra của một hệ thống tuyến tính bất biến theo thời gian (LTI). Bài viết này sẽ cung cấp cho bạn cái nhìn tổng quan về hàm truyền đạt, cách xác định hàm truyền đạt từ phương trình vi phân hoặc sơ đồ khối, cùng với những bài tập có lời giải chi tiết giúp bạn nắm vững kiến thức.
Hàm Truyền Đạt Là Gì?
Hàm truyền đạt (transfer function) của một hệ thống LTI là tỷ số Laplace của đầu ra (output) trên đầu vào (input) trong miền Laplace, với điều kiện ban đầu bằng không.
Xác Định Hàm Truyền Đạt
Có hai cách chính để xác định hàm truyền đạt của một hệ thống:
1. Từ phương trình vi phân:
- Bước 1: Biến đổi Laplace cả hai vế của phương trình vi phân, với điều kiện ban đầu bằng không.
- Bước 2: Biểu diễn phương trình theo tỷ số Laplace của đầu ra trên đầu vào.
2. Từ sơ đồ khối:
- Bước 1: Rút gọn sơ đồ khối bằng cách sử dụng các quy tắc biến đổi sơ đồ khối.
- Bước 2: Xác định hàm truyền đạt từ sơ đồ khối rút gọn.
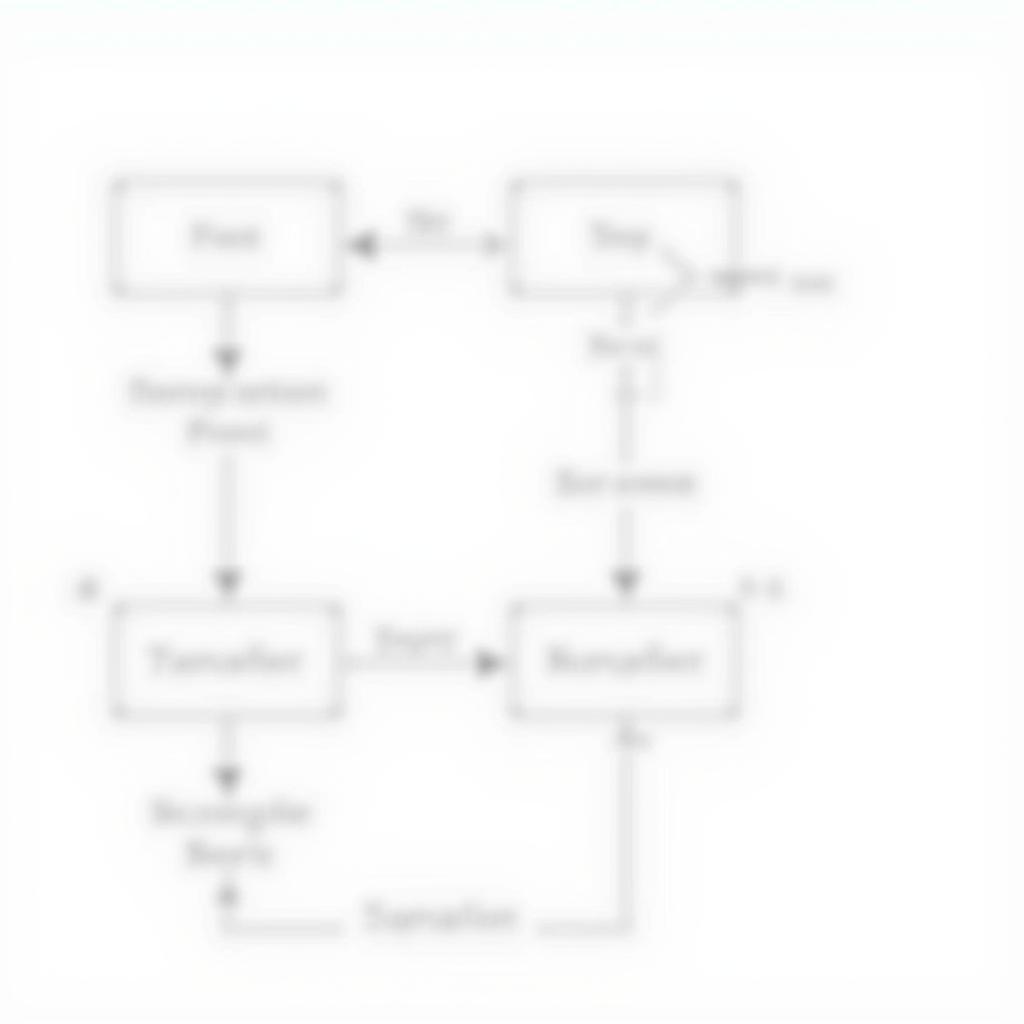 Xác định Hàm Truyền Đạt từ Sơ Đồ Khối
Xác định Hàm Truyền Đạt từ Sơ Đồ Khối
Bài Tập Tìm Hàm Truyền Đạt Có Lời Giải
Bài tập 1: Xác định hàm truyền đạt của hệ thống có phương trình vi phân sau:
y''(t) + 3y'(t) + 2y(t) = u(t)Lời giải:
- Bước 1: Biến đổi Laplace cả hai vế của phương trình:
s^2Y(s) + 3sY(s) + 2Y(s) = U(s)- Bước 2: Tìm tỷ số Laplace của đầu ra trên đầu vào:
Y(s)/U(s) = 1/(s^2 + 3s + 2)Vậy, hàm truyền đạt của hệ thống là G(s) = 1/(s^2 + 3s + 2)
Bài tập 2: Xác định hàm truyền đạt của hệ thống được biểu diễn bởi sơ đồ khối sau:
Lời giải:
-
Bước 1: Rút gọn sơ đồ khối:
-
Bước 2: Xác định hàm truyền đạt từ sơ đồ khối rút gọn:
G(s) = (G1(s)G2(s))/(1 + G1(s)G2(s)H(s))Bài tập 3: Một hệ thống có hàm truyền đạt G(s) = 1/(s+1)(s+2). Xác định đáp ứng xung của hệ thống.
Lời giải:
- Đáp ứng xung là biến đổi Laplace ngược của hàm truyền đạt.
- Phân tích hàm truyền đạt thành các phần tử đơn giản: G(s) = A/(s+1) + B/(s+2)
- Tìm A và B bằng phương pháp hệ số bất định hoặc phương pháp Heaviside.
- Biến đổi Laplace ngược từng phần tử đơn giản để tìm đáp ứng xung.
Ứng Dụng Của Hàm Truyền Đạt
Hàm truyền đạt có nhiều ứng dụng quan trọng trong lĩnh vực điều khiển tự động, bao gồm:
- Phân tích tính ổn định của hệ thống.
- Thiết kế bộ điều khiển.
- Mô phỏng hệ thống.
- Phân tích đáp ứng tần số.
Kết Luận
Bài viết đã cung cấp cho bạn kiến thức cơ bản về hàm truyền đạt và cách xác định hàm truyền đạt từ phương trình vi phân hoặc sơ đồ khối. Bằng cách luyện tập các bài tập có lời giải, bạn có thể tự tin vận dụng kiến thức vào việc phân tích và thiết kế các hệ thống điều khiển tự động.
Câu Hỏi Thường Gặp
1. Hàm truyền đạt có ý nghĩa gì trong thực tế?
Hàm truyền đạt giúp chúng ta hiểu được mối quan hệ giữa đầu vào và đầu ra của một hệ thống. Ví dụ, trong hệ thống điều khiển nhiệt độ, hàm truyền đạt cho biết nhiệt độ phòng thay đổi như thế nào khi ta thay đổi giá trị đặt của bộ điều khiển.
2. Làm thế nào để kiểm tra tính ổn định của một hệ thống dựa vào hàm truyền đạt?
Có nhiều phương pháp để kiểm tra tính ổn định của hệ thống, ví dụ như tiêu chuẩn Routh-Hurwitz, tiêu chuẩn Nyquist, … Các tiêu chuẩn này dựa trên vị trí của các cực của hàm truyền đạt trên mặt phẳng phức.
3. Hàm truyền đạt có thể được sử dụng để thiết kế bộ điều khiển PID không?
Có, hàm truyền đạt là một công cụ quan trọng trong việc thiết kế bộ điều khiển PID. Các thông số của bộ điều khiển PID (Kp, Ki, Kd) có thể được xác định dựa trên hàm truyền đạt của hệ thống cần điều khiển.
Bạn Cần Thêm Thông Tin?
Để tìm hiểu thêm về các chủ đề liên quan, bạn có thể tham khảo các bài viết sau:
Hãy Liên Hệ Với Chúng Tôi
Nếu bạn cần hỗ trợ, hãy liên hệ Số Điện Thoại: 02033846993, Email: [email protected] Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
