Giải Phương Trình Và Bất Phương Trình là một trong những nội dung quan trọng của toán học, được ứng dụng rộng rãi trong nhiều lĩnh vực từ khoa học, kỹ thuật đến kinh tế và đời sống. Bài viết này sẽ cung cấp cho bạn cái nhìn tổng quan và chi tiết về phương pháp giải phương trình và bất phương trình, cùng với những ví dụ minh họa dễ hiểu.
Phân Loại Phương Trình và Bất Phương Trình
Tùy thuộc vào dạng biểu thức và số ẩn, ta có thể phân loại phương trình và bất phương trình thành nhiều loại khác nhau. Dưới đây là một số loại phổ biến:
Phương trình bậc nhất một ẩn
Phương trình bậc nhất một ẩn có dạng ax + b = 0, với a và b là các số thực, a ≠ 0.
Ví dụ: 2x + 3 = 0, -5x + 1 = 0.
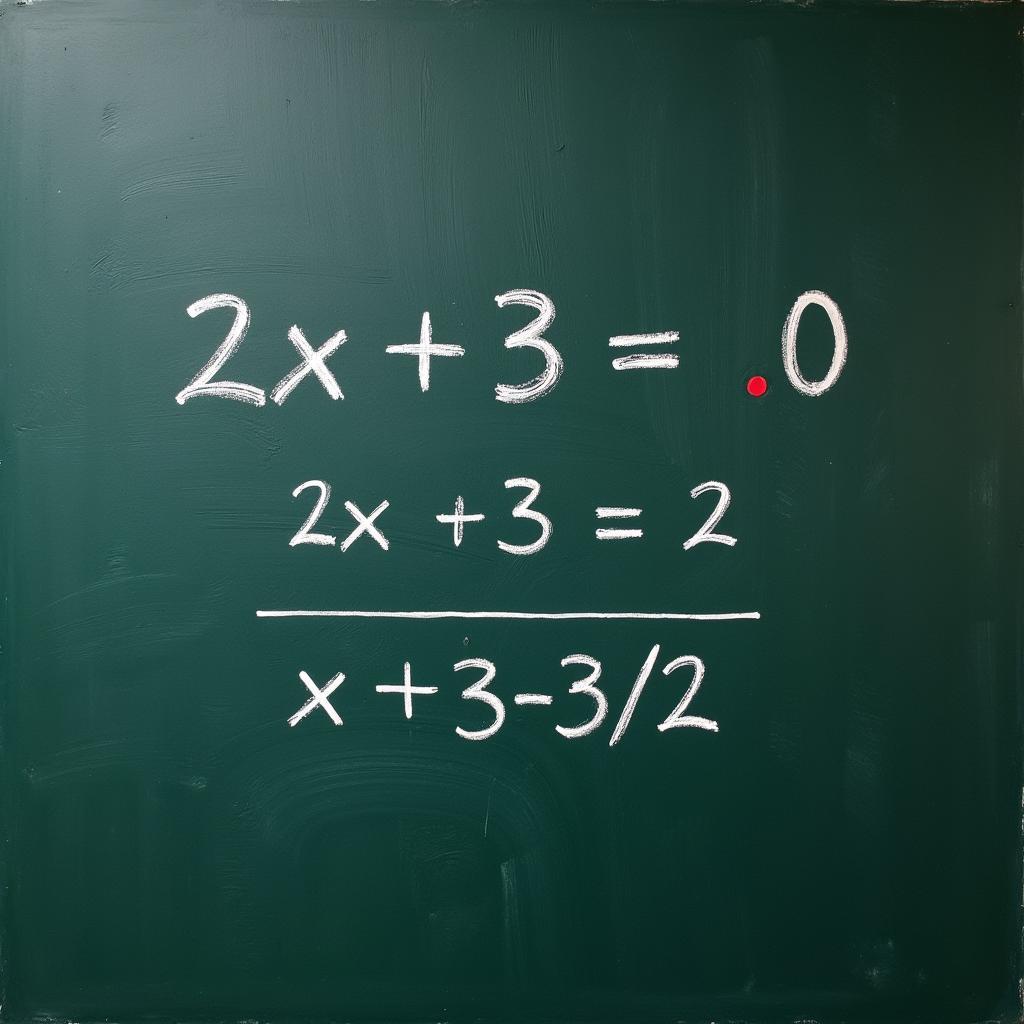 Giải phương trình bậc nhất một ẩn
Giải phương trình bậc nhất một ẩn
Phương trình bậc hai một ẩn
Phương trình bậc hai một ẩn có dạng ax² + bx + c = 0, với a, b và c là các số thực, a ≠ 0.
Ví dụ: x² + 2x – 3 = 0, -2x² + 5x + 1 = 0.
Hệ phương trình bậc nhất hai ẩn
Hệ phương trình bậc nhất hai ẩn gồm hai phương trình bậc nhất hai ẩn, có dạng:
a1x + b1y = c1
a2x + b2y = c2Ví dụ:
2x + 3y = 5
x - y = 1Bất phương trình bậc nhất một ẩn
Bất phương trình bậc nhất một ẩn có dạng ax + b > 0 (hoặc <, ≥, ≤), với a và b là các số thực, a ≠ 0.
Ví dụ: 3x – 2 > 0, -x + 4 ≤ 0.
Các Phương Pháp Giải Phương Trình và Bất Phương Trình
Giải phương trình bậc nhất một ẩn
Để giải phương trình bậc nhất một ẩn ax + b = 0, ta thực hiện các bước sau:
- Chuyển vế đổi dấu: ax = -b
- Chia hai vế cho a (khác 0): x = -b/a
Ví dụ: Giải phương trình 3x – 2 = 7
- Chuyển vế đổi dấu: 3x = 7 + 2 = 9
- Chia hai vế cho 3: x = 9/3 = 3
Vậy nghiệm của phương trình là x = 3.
Để tìm hiểu thêm về các phương pháp giải phương trình và bất phương trình khác, bạn có thể tham khảo giải phương trình và bất phương trình lớp 9.
Giải phương trình bậc hai một ẩn
Có nhiều cách để giải phương trình bậc hai một ẩn, bao gồm:
- Công thức nghiệm: Áp dụng công thức nghiệm tổng quát để tìm nghiệm.
- Phân tích thành nhân tử: Phân tích vế trái thành tích của hai biểu thức bậc nhất.
- Sử dụng định lý Vi-ét: Áp dụng định lý Vi-ét để tìm tổng và tích của hai nghiệm.
Ví dụ: Giải phương trình x² – 5x + 6 = 0 bằng phương pháp phân tích thành nhân tử:
- Phân tích vế trái thành nhân tử: (x – 2)(x – 3) = 0
- Cho từng nhân tử bằng 0: x – 2 = 0 hoặc x – 3 = 0
- Giải các phương trình bậc nhất: x = 2 hoặc x = 3
Vậy nghiệm của phương trình là x = 2 hoặc x = 3.
 Giải phương trình bậc hai một ẩn
Giải phương trình bậc hai một ẩn
Giải hệ phương trình bậc nhất hai ẩn
Các phương pháp thường được sử dụng để giải hệ phương trình bậc nhất hai ẩn bao gồm:
- Phương pháp thế: Rút một ẩn từ một phương trình theo ẩn còn lại, sau đó thế vào phương trình còn lại.
- Phương pháp cộng đại số: Cộng hoặc trừ hai vế của hai phương trình để triệt tiêu một ẩn.
Giải bất phương trình bậc nhất một ẩn
Để giải bất phương trình bậc nhất một ẩn, ta thực hiện các bước tương tự như giải phương trình bậc nhất một ẩn. Tuy nhiên, cần lưu ý quy tắc đổi dấu khi chia hoặc nhân hai vế cho một số âm.
Ví dụ: Giải bất phương trình 2x – 3 < 7
- Chuyển vế đổi dấu: 2x < 7 + 3 = 10
- Chia hai vế cho 2: x < 5
Vậy tập nghiệm của bất phương trình là x < 5.
Ứng Dụng của Giải Phương Trình và Bất Phương Trình
Giải phương trình và bất phương trình có ứng dụng rộng rãi trong nhiều lĩnh vực:
- Vật lý: Tính toán vận tốc, gia tốc, quãng đường, thời gian,…
- Hóa học: Xác định nồng độ dung dịch, tính toán lượng chất tham gia phản ứng,…
- Kinh tế: Tìm mức sản xuất tối ưu, tính toán lãi suất, dự báo doanh thu,…
- Lập trình: Xây dựng thuật toán, giải quyết bài toán tối ưu,…
Kết Luận
Giải phương trình và bất phương trình là một phần kiến thức quan trọng trong toán học, có ứng dụng rộng rãi trong thực tế. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về phương pháp giải phương trình và bất phương trình, từ đó áp dụng hiệu quả vào học tập và công việc.
Câu hỏi thường gặp
1. Khi nào phương trình bậc hai một ẩn vô nghiệm?
Phương trình bậc hai một ẩn ax² + bx + c = 0 vô nghiệm khi và chỉ khi Δ = b² – 4ac < 0.
2. Hệ phương trình bậc nhất hai ẩn có bao nhiêu nghiệm?
Hệ phương trình bậc nhất hai ẩn có thể có một nghiệm duy nhất, vô số nghiệm hoặc vô nghiệm.
3. Làm thế nào để kiểm tra xem một số có phải là nghiệm của bất phương trình hay không?
Thay số đó vào bất phương trình, nếu bất đẳng thức đúng thì số đó là nghiệm của bất phương trình.
Bạn có muốn tìm hiểu thêm về 3x 2 5 giải phương trình và bất phương trình? Hay bạn đang gặp khó khăn với bài tập logarit có lời giải? Hãy khám phá thêm nhiều kiến thức bổ ích về toán giải trên website của chúng tôi.
Bạn cần hỗ trợ?
Liên hệ ngay với chúng tôi:
- Số Điện Thoại: 02033846993
- Email: [email protected]
- Địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam.
Đội ngũ chăm sóc khách hàng của chúng tôi luôn sẵn sàng hỗ trợ bạn 24/7!
