Biểu đồ Bode là một công cụ quan trọng trong lĩnh vực kỹ thuật điều khiển và phân tích hệ thống, giúp chúng ta hình dung và phân tích đáp ứng tần số của một hệ thống tuyến tính bất biến theo thời gian (LTI). Việc thành thạo kỹ năng vẽ và phân tích biểu đồ Bode là rất cần thiết để thiết kế và tối ưu hóa hệ thống điều khiển hiệu quả. Bài viết này sẽ cung cấp cho bạn những kiến thức cơ bản về biểu đồ Bode, cũng như hướng dẫn chi tiết cách vẽ biểu đồ Bode có lời giải cho các bài tập cụ thể.
Biểu đồ Bode là gì?
Biểu đồ Bode là một loại biểu đồ thể hiện đáp ứng tần số của một hệ thống LTI. Nó bao gồm hai đồ thị riêng biệt:
- Biểu đồ Bode biên độ: Thể hiện biên độ của đáp ứng tần số (thường được biểu diễn bằng decibel – dB) theo tần số (thường được biểu diễn bằng thang logarit).
- Biểu đồ Bode pha: Thể hiện pha của đáp ứng tần số (được biểu diễn bằng độ) theo tần số (cũng được biểu diễn bằng thang logarit).
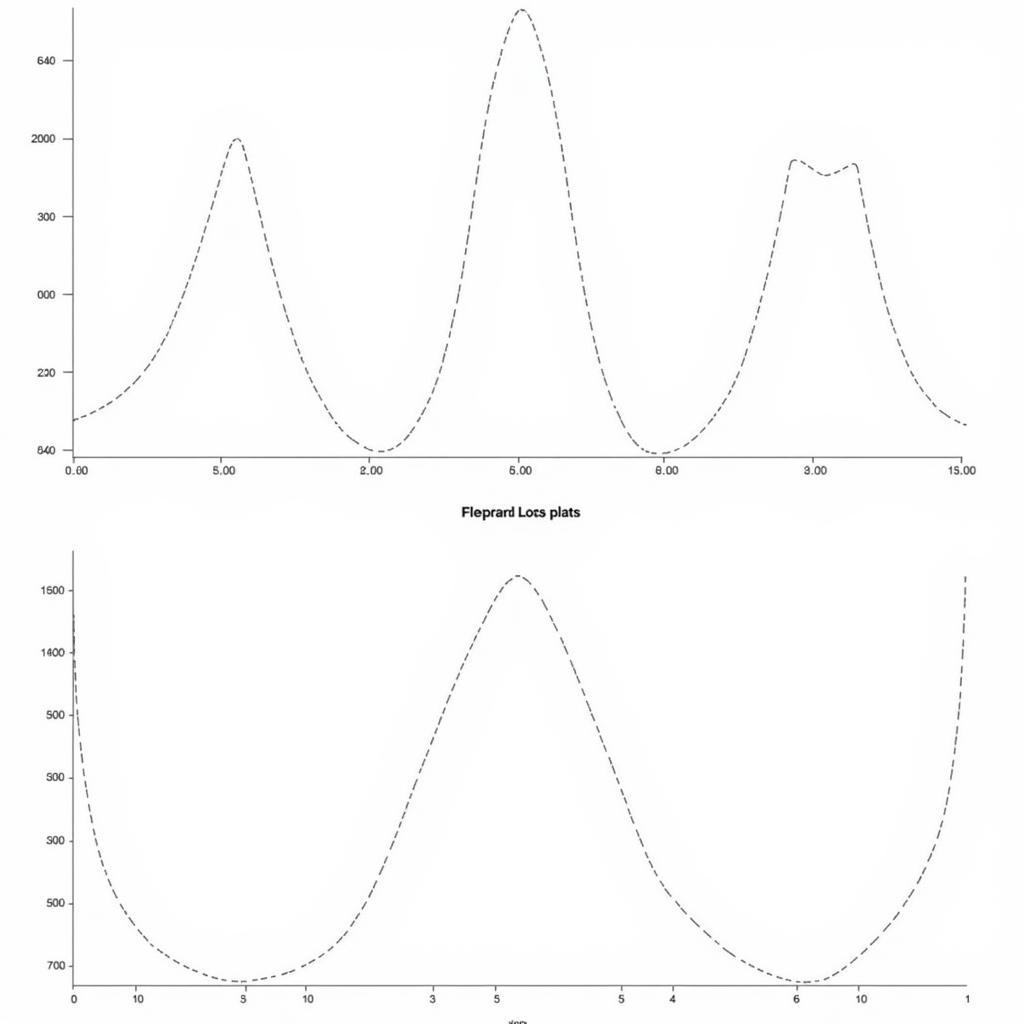 Basic Bode Plot
Basic Bode Plot
Tại sao cần vẽ biểu đồ Bode?
Biểu đồ Bode cung cấp nhiều thông tin hữu ích về một hệ thống, bao gồm:
- Độ khuếch đại (gain): Cho biết hệ thống khuếch đại hoặc suy giảm tín hiệu đầu vào ở các tần số khác nhau.
- Pha (phase): Cho biết sự dịch pha giữa tín hiệu đầu vào và đầu ra ở các tần số khác nhau.
- Băng thông (bandwidth): Cho biết dải tần số mà hệ thống có thể truyền qua với độ khuếch đại chấp nhận được.
- Độ ổn định (stability): Giúp xác định xem hệ thống có ổn định hay không dựa vào biên độ và pha ở tần số cắt.
Các bước vẽ biểu đồ Bode có lời giải
1. Xác định hàm truyền đạt của hệ thống
Hàm truyền đạt là một mô hình toán học biểu diễn mối quan hệ giữa tín hiệu đầu vào và đầu ra của một hệ thống. Nó thường được biểu diễn dưới dạng tỷ số của hai đa thức theo biến số phức s.
Ví dụ: Hàm truyền đạt của một mạch RC đơn giản là:
G(s) = 1 / (RCs + 1)2. Xác định các cực và zero của hàm truyền đạt
Cực (pole) là những giá trị của s làm cho mẫu số của hàm truyền đạt bằng 0. Zero là những giá trị của s làm cho tử số của hàm truyền đạt bằng 0.
Ví dụ: Hàm truyền đạt G(s) ở trên có một cực tại s = -1/RC và không có zero.
3. Vẽ biểu đồ Bode biên độ
- Bước 3.1: Xác định độ lợi DC (tần số bằng 0).
- Bước 3.2: Vẽ đường tiệm cận biên độ cho mỗi cực và zero.
- Bước 3.3: Xác định điểm gãy của đường tiệm cận.
- Bước 3.4: Vẽ đường cong thực tế dựa trên các đường tiệm cận.
 Drawing Magnitude Bode Plot
Drawing Magnitude Bode Plot
4. Vẽ biểu đồ Bode pha
- Bước 4.1: Xác định pha ban đầu (tại tần số rất thấp).
- Bước 4.2: Vẽ đường tiệm cận pha cho mỗi cực và zero.
- Bước 4.3: Xác định điểm gãy của đường tiệm cận.
- Bước 4.4: Vẽ đường cong thực tế dựa trên các đường tiệm cận.
 Drawing Phase Bode Plot
Drawing Phase Bode Plot
Ví dụ bài tập vẽ biểu đồ Bode có lời giải
Bài tập: Vẽ biểu đồ Bode cho hàm truyền đạt sau:
G(s) = (s + 1) / (s(s + 10))Lời giải:
Bước 1: Xác định cực và zero:
- Zero: s = -1
- Cực: s = 0, s = -10
Bước 2: Vẽ biểu đồ Bode biên độ:
- Độ lợi DC: 20*log10(1/10) = -20 dB
- Vẽ đường tiệm cận biên độ cho zero tại s = -1 (tăng 20 dB/decade từ tần số góc ω = 1 rad/s).
- Vẽ đường tiệm cận biên độ cho cực tại s = 0 (giảm 20 dB/decade từ tần số góc ω = 0.1 rad/s).
- Vẽ đường tiệm cận biên độ cho cực tại s = -10 (giảm 20 dB/decade từ tần số góc ω = 10 rad/s).
- Nối các đường tiệm cận để có đường cong biên độ thực tế.
Bước 3: Vẽ biểu đồ Bode pha:
- Pha ban đầu: -90 độ (do cực tại s=0).
- Vẽ đường tiệm cận pha cho zero tại s = -1 (tăng 45 độ/decade từ tần số góc ω = 0.1 rad/s đến ω = 10 rad/s).
- Vẽ đường tiệm cận pha cho cực tại s = -10 (giảm 45 độ/decade từ tần số góc ω = 1 rad/s đến ω = 100 rad/s).
- Nối các đường tiệm cận để có đường cong pha thực tế.
Kết luận
Bài viết đã cung cấp những kiến thức cơ bản về biểu đồ Bode và hướng dẫn chi tiết cách vẽ biểu đồ Bode có lời giải. Hy vọng bài viết này hữu ích cho bạn trong việc học tập và nghiên cứu về kỹ thuật điều khiển và phân tích hệ thống.
FAQ
1. Biểu đồ Bode được sử dụng trong những ứng dụng thực tế nào?
Biểu đồ Bode được sử dụng rộng rãi trong thiết kế và phân tích hệ thống điều khiển, mạch điện tử, xử lý tín hiệu âm thanh và hình ảnh, và nhiều lĩnh vực khác.
2. Làm thế nào để xác định độ ổn định của hệ thống từ biểu đồ Bode?
Độ ổn định của hệ thống có thể được đánh giá bằng cách xem xét biên độ và pha của hàm truyền đạt tại tần số cắt. Nếu biên độ dương và pha lớn hơn -180 độ, hệ thống được coi là ổn định.
Bạn cần hỗ trợ?
Liên hệ với chúng tôi:
Số Điện Thoại: 02033846993
Email: [email protected]
Hoặc đến địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam.
Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
