Bài tập hình bình hành lớp 8 là một phần quan trọng trong chương trình toán học, giúp học sinh nắm vững kiến thức về hình học phẳng và phát triển khả năng tư duy logic. Bài viết này sẽ cung cấp cho bạn những kiến thức cơ bản về hình bình hành, kèm theo lời giải chi tiết cho các dạng bài tập thường gặp.
Hình Bình Hành Là Gì?
Hình bình hành là tứ giác có các cạnh đối song song và bằng nhau.
Để chứng minh một tứ giác là hình bình hành, ta có thể dựa vào các dấu hiệu nhận biết sau:
- Dấu hiệu 1: Tứ giác có các cạnh đối song song.
- Dấu hiệu 2: Tứ giác có các cạnh đối bằng nhau.
- Dấu hiệu 3: Tứ giác có hai cạnh đối vừa song song vừa bằng nhau.
- Dấu hiệu 4: Tứ giác có các góc đối bằng nhau.
- Dấu hiệu 5: Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Các Dạng Bài Tập Hình Bình Hành Lớp 8
Dưới đây là một số dạng bài tập hình bình hành lớp 8 thường gặp:
Dạng 1: Chứng minh tứ giác là hình bình hành
Bài tập: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Chứng minh tứ giác DECB là hình bình hành.
Lời giải:
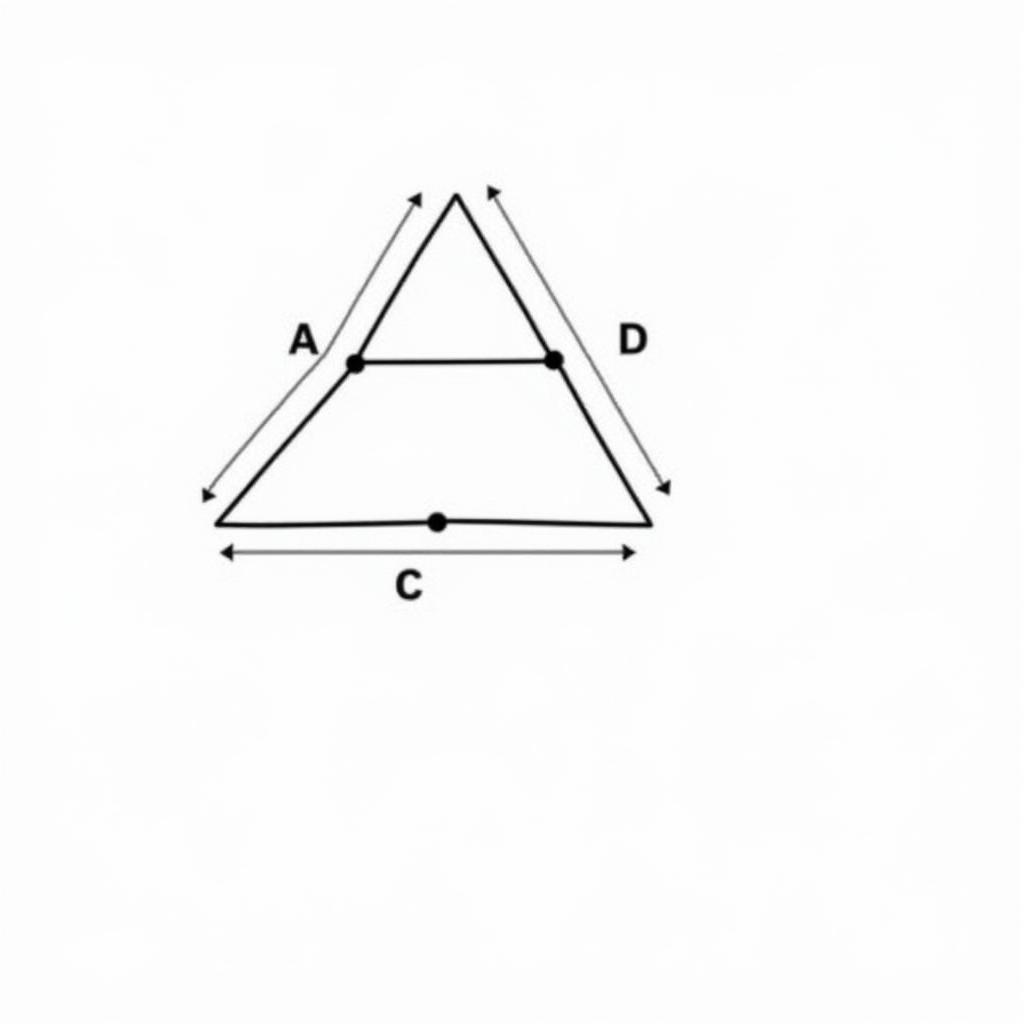 hình minh họa bài tập chứng minh tứ giác là hình bình hành
hình minh họa bài tập chứng minh tứ giác là hình bình hành
Vì D là trung điểm AB, E là trung điểm AC (giả thiết)
=> DE là đường trung bình của tam giác ABC
=> DE // BC và DE = 1/2 BC (tính chất đường trung bình)
Mà DB = 1/2 AB và CE = 1/2 AC (D, E là trung điểm)
=> DE = DB và DE = CE
Do đó, tứ giác DECB có DE // BC và DE = BC
=> Tứ giác DECB là hình bình hành (dấu hiệu nhận biết 3)
Dạng 2: Tính toán độ dài cạnh, góc, chu vi, diện tích hình bình hành
Bài tập: Cho hình bình hành ABCD có AB = 10cm, AD = 6cm, góc BAD = 60 độ. Tính độ dài đường chéo BD và diện tích hình bình hành ABCD.
Lời giải:
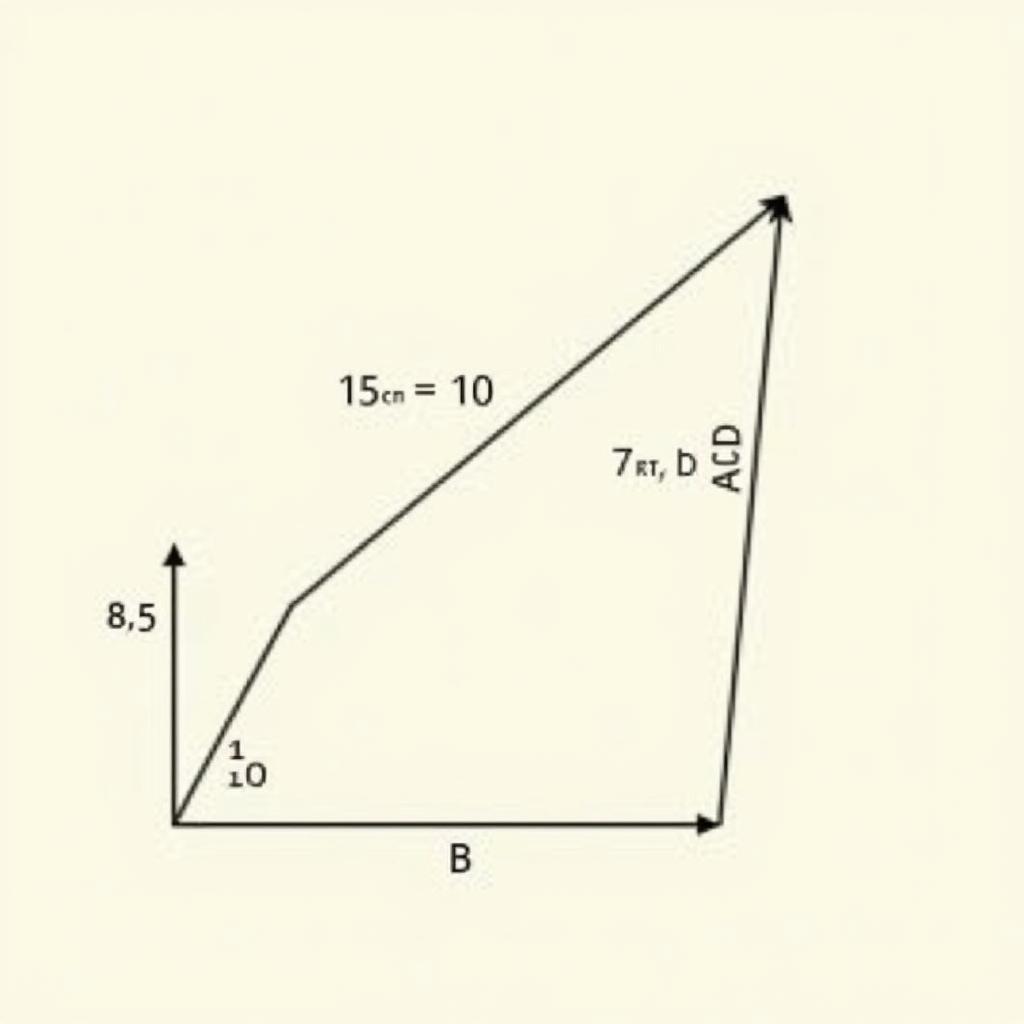 hình minh họa bài tập tính toán độ dài cạnh, góc, chu vi, diện tích hình bình hành
hình minh họa bài tập tính toán độ dài cạnh, góc, chu vi, diện tích hình bình hành
Xét tam giác ABD, ta có:
- AB = 10cm, AD = 6cm
- góc BAD = 60 độ
Áp dụng định lý cosin cho tam giác ABD, ta có:
BD² = AB² + AD² – 2.AB.AD.cos(BAD)
BD² = 10² + 6² – 2.10.6.cos(60°)
BD² = 52
=> BD = 2√13 cm
Diện tích hình bình hành ABCD là:
S = AB.AD.sin(BAD) = 10.6.sin(60°) = 30√3 cm²
Dạng 3: Chứng minh các tính chất của hình bình hành
Bài tập: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh:
a) AMCN là hình bình hành
b) Ba điểm M, O, N thẳng hàng (với O là giao điểm hai đường chéo AC và BD)
Lời giải:
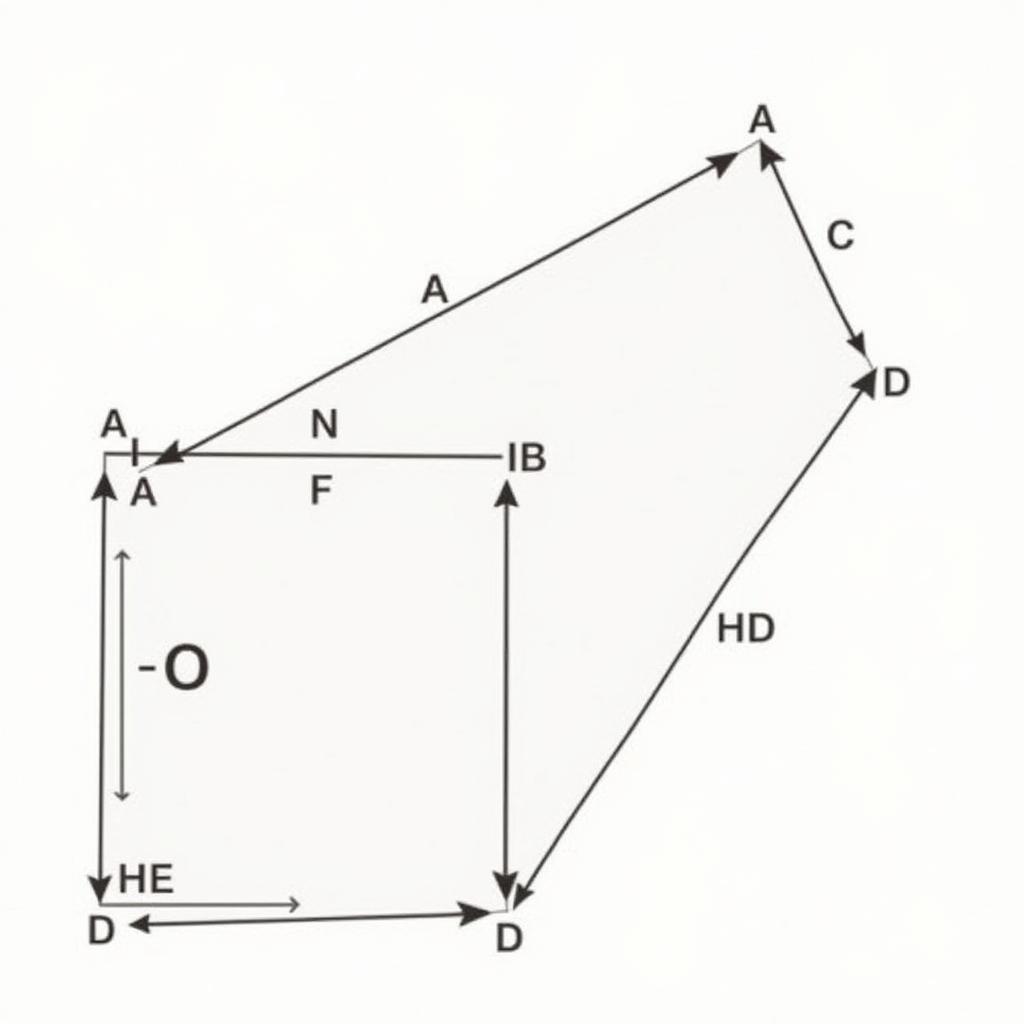 hình minh họa bài tập chứng minh các tính chất của hình bình hành
hình minh họa bài tập chứng minh các tính chất của hình bình hành
a) Vì ABCD là hình bình hành:
=> AB // CD và AB = CD (tính chất hình bình hành)
Mà AM = 1/2 AB và CN = 1/2 CD (M, N là trung điểm)
=> AM = CN và AM // CN
Do đó, tứ giác AMCN là hình bình hành (dấu hiệu nhận biết 3)
b) Vì ABCD là hình bình hành nên hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường (tính chất hình bình hành)
Tương tự, vì AMCN là hình bình hành nên hai đường chéo AC và MN cũng cắt nhau tại trung điểm O của mỗi đường (tính chất hình bình hành)
=> Ba điểm M, O, N thẳng hàng.
Kết luận
Bài viết đã cung cấp cho bạn kiến thức cơ bản về hình bình hành và lời giải chi tiết cho một số dạng bài tập lớp 8. Hy vọng bài viết này sẽ giúp bạn tự tin hơn khi giải bài tập hình học.
FAQ
1. Làm thế nào để phân biệt hình bình hành với các hình tứ giác khác?
Hình bình hành có các cạnh đối song song và bằng nhau, đây là đặc điểm quan trọng để phân biệt với các hình tứ giác khác như hình thang, hình chữ nhật, hình thoi.
2. Có bao nhiêu cách để chứng minh một tứ giác là hình bình hành?
Có 5 dấu hiệu nhận biết hình bình hành, bạn có thể sử dụng bất kỳ dấu hiệu nào phù hợp với dữ kiện bài toán để chứng minh.
3. Diện tích hình bình hành được tính như thế nào?
Diện tích hình bình hành bằng độ dài một cạnh nhân với chiều cao tương ứng với cạnh đó.
4. Hình bình hành có những tính chất gì đặc biệt?
Hình bình hành có các cạnh đối song song và bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
5. Ngoài các dạng bài tập đã nêu, còn có dạng bài tập hình bình hành nào khác?
Còn rất nhiều dạng bài tập hình bình hành khác, ví dụ như chứng minh hai đường thẳng song song, chứng minh ba điểm thẳng hàng, tìm vị trí của điểm để thỏa mãn điều kiện cho trước…
Bạn cần hỗ trợ?
Liên hệ ngay với Giải Bóng!
- Số Điện Thoại: 02033846993
- Email: [email protected]
- Địa chỉ: X2FW+GGM, Cái Lân, Bãi Cháy, Hạ Long, Quảng Ninh, Việt Nam.
Đội ngũ chúng tôi luôn sẵn sàng hỗ trợ bạn 24/7!
