Giải chuỗi phương trình là một trong những dạng bài tập quan trọng trong chương trình toán học lớp 8 và lớp 9. Nắm vững phương pháp giải chuỗi phương trình không chỉ giúp học sinh đạt điểm cao trong các kỳ thi mà còn rèn luyện tư duy logic và khả năng giải quyết vấn đề.
Hệ Phương Trình – Nền Tảng Cho Việc Giải Chuỗi Phương Trình
Trước khi đi vào tìm hiểu cách giải chuỗi phương trình, chúng ta cần nắm vững kiến thức về hệ phương trình. Hệ phương trình là tập hợp hai hay nhiều phương trình có chung một tập nghiệm.
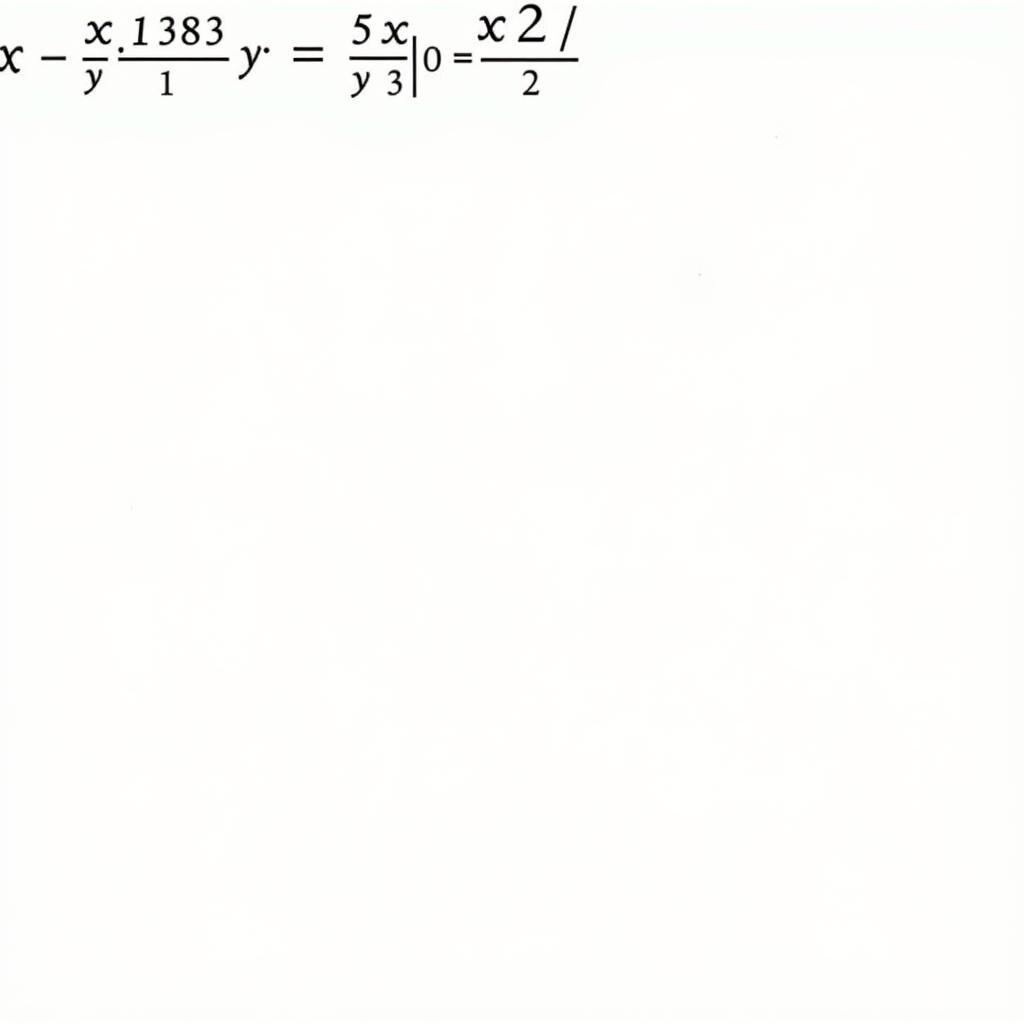 Giải Hệ Phương Trình Bậc Nhất Hai Ẩn
Giải Hệ Phương Trình Bậc Nhất Hai Ẩn
Các Phương Pháp Giải Hệ Phương Trình Phổ Biến:
- Phương pháp thế: Biểu diễn một ẩn theo ẩn khác từ một phương trình, sau đó thế vào phương trình còn lại.
- Phương pháp cộng đại số: Cộng hoặc trừ hai vế của các phương trình đã cho để triệt tiêu một ẩn, từ đó tìm ra giá trị của ẩn còn lại.
- Phương pháp đồ thị: Biểu diễn đồ thị của mỗi phương trình trong hệ trục tọa độ, giao điểm của các đồ thị là nghiệm của hệ phương trình.
Giải Chuỗi Phương Trình – Nâng Cao Khả Năng Giải Toán
Chuỗi phương trình là hệ phương trình đặc biệt, trong đó mỗi phương trình chứa một hoặc nhiều ẩn giống nhau. Việc giải chuỗi phương trình đòi hỏi học sinh phải vận dụng linh hoạt các phương pháp giải hệ phương trình đã học kết hợp với tư duy logic.
Các Bước Giải Chuỗi Phương Trình:
- Nhận dạng chuỗi phương trình: Xác định các ẩn số và mối liên hệ giữa chúng trong các phương trình.
- Chọn phương pháp giải phù hợp: Tùy thuộc vào dạng cụ thể của chuỗi phương trình, ta có thể lựa chọn phương pháp thế, cộng đại số hoặc kết hợp cả hai.
- Giải hệ phương trình: Áp dụng phương pháp đã chọn để tìm ra giá trị của các ẩn số.
- Kiểm tra nghiệm: Thay các giá trị tìm được vào chuỗi phương trình ban đầu để kiểm tra xem chúng có thỏa mãn hay không.
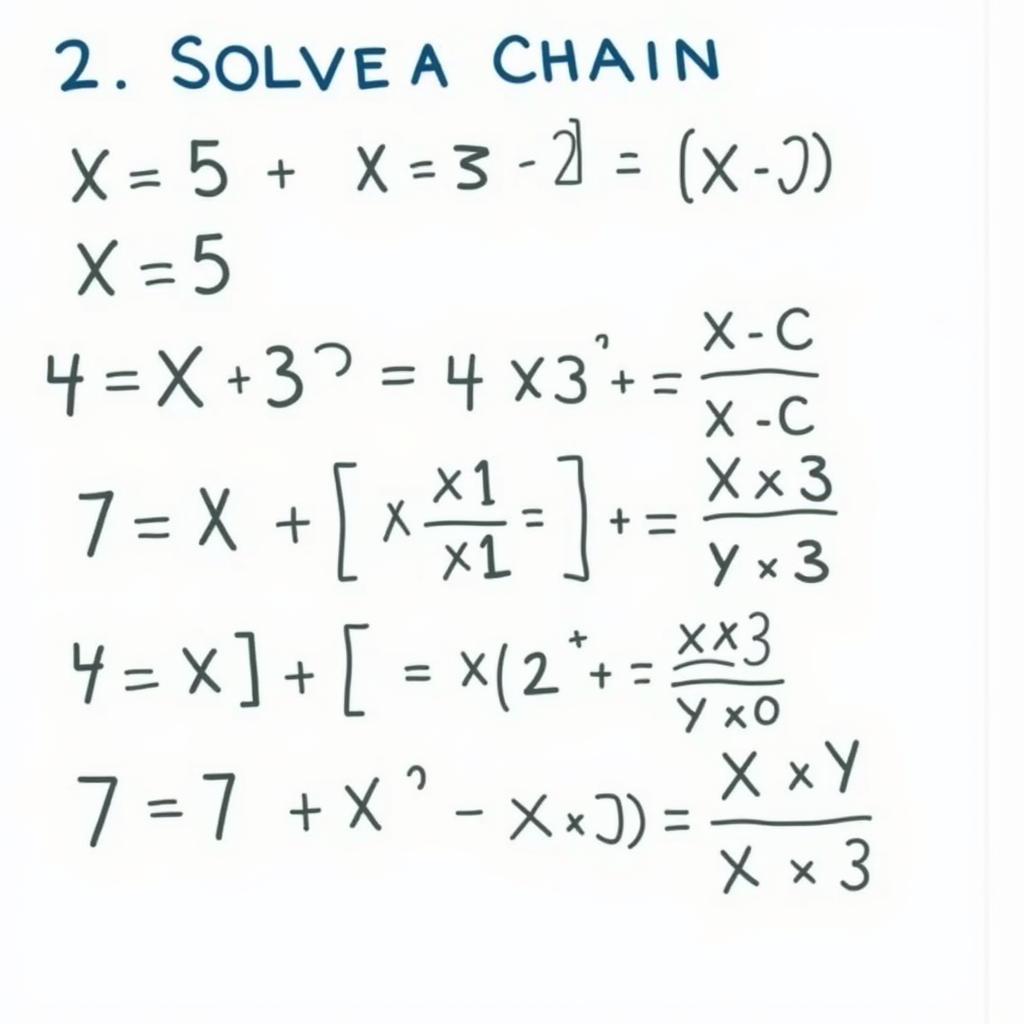 Giải Chuỗi Phương Trình Bậc Nhất
Giải Chuỗi Phương Trình Bậc Nhất
Ví dụ Minh Họa
Giải chuỗi phương trình sau:
x + 2y = 5 (1)
2y – 3z = 1 (2)
x + 3z = 4 (3)
Bước 1: Nhận dạng, đây là chuỗi phương trình 3 ẩn x, y, z.
Bước 2: Ta có thể sử dụng phương pháp thế. Từ phương trình (1), rút ra x = 5 – 2y, thế vào phương trình (3) ta được:
5 – 2y + 3z = 4
=> -2y + 3z = -1 (4)
Bây giờ ta có hệ phương trình (2) và (4):
2y – 3z = 1
-2y + 3z = -1
Bước 3: Cộng hai phương trình (2) và (4) ta được 0 = 0 (luôn đúng). Điều này có nghĩa là hệ phương trình có vô số nghiệm.
Bước 4: Biểu diễn nghiệm của hệ phương trình. Chọn z = t (t là số thực bất kỳ), từ phương trình (2) ta có y = (3t + 1)/2. Thay y và z vào phương trình (1) ta được x = 4 – 3t.
Vậy, nghiệm của chuỗi phương trình là (x, y, z) = (4 – 3t, (3t + 1)/2, t) với t là số thực bất kỳ.
Mẹo Giải Chuỗi Phương Trình Hiệu Quả
- Rèn luyện khả năng quan sát và nhận dạng dạng của chuỗi phương trình.
- Nắm vững các phương pháp giải hệ phương trình cơ bản.
- Luyện tập giải nhiều bài tập với độ khó tăng dần.
- Tham khảo các tài liệu và bài giảng trực tuyến.
 Ứng Dụng Giải Chuỗi Phương Trình Vào Thực Tế
Ứng Dụng Giải Chuỗi Phương Trình Vào Thực Tế
Kết Luận
Giải chuỗi phương trình là một kỹ năng toán học quan trọng, đòi hỏi sự kết hợp giữa kiến thức và kỹ năng tính toán. Bằng cách luyện tập thường xuyên, học sinh sẽ nắm vững phương pháp giải và tự tin hơn khi giải quyết các bài tập liên quan đến chuỗi phương trình lớp 8,9.
